Участник:Dmitry/Плотностный алгоритм кластеризации: различия между версиями
Dmitry (обсуждение | вклад) (Новая страница: «Авторы описания: Титов Д.Е. = Свойства и структура алгоритма = == Общее оп…») |
Dmitry (обсуждение | вклад) |
||
| Строка 4: | Строка 4: | ||
== Общее описание алгоритма == | == Общее описание алгоритма == | ||
| + | |||
| + | Под кластеризацией понимается деление заданного множества точек данных (объектов) на подгруппы, каждая из которых, насколько это возможно, однородна. В основе метода кластеризации DBSCAN лежит объединение некоторых объектов в соответствии с их внутригрупповым «соединением». Для проведения корректной процедуры кластеризации необходимо указать критерии, по которым объекты будут объединены в кластеры. Прежде всего, необходимо сказать, что кластеры представляют собой плотные области некоторых объектов в пространстве данных, разделенных между собой объектами, плотность которых значительно ниже. Расположение точек в одном кластере обусловлено их соединением, т.е. некоторой связью между собой. | ||
| + | |||
| + | == Математическое описание алгоритма == | ||
| + | |||
| + | Плотность точек для данной точки <math>X</math> определяется двумя параметрами. Первым из них является | ||
| + | <math>\varepsilon</math> – радиус «соседства» (приближенности) точки <math>X</math>. Тогда множество <math>M(X)</math> будет включать в себя такие точки | ||
| + | n,1i,f | ||
| + | i | ||
| + | , для которых следующее не- | ||
| + | равенство будет истинно | ||
| + | n,1i,f,Xdist | ||
| + | i . (1). | ||
| + | Функция | ||
| + | )2var,1(vardist | ||
| + | определяет расстоя- | ||
| + | ние между объектами выборки | ||
| + | D | ||
| + | . Это расстояние | ||
| + | может вычисляться различными способами, | ||
| + | например, как евклидово расстояние или с помо- | ||
| + | щью метрики Минковского. | ||
| + | Вторым параметром определения плотности | ||
| + | точек является MCP – это минимальное количество | ||
| + | точек, которые расположены ближе всего к данной | ||
| + | точке согласно определенному радиусу . | ||
| + | Точка | ||
| + | n,1i,f | ||
| + | i | ||
| + | будет являться окруженной | ||
| + | точкой (согласно | ||
| + | | ||
| + | и | ||
| + | MCP | ||
| + | ) если | ||
| + | | ||
| + | MCPX . (2) | ||
| + | Это значит, что точка | ||
| + | n,1i,f | ||
| + | i | ||
| + | окружен- | ||
| + | ная, если количество «соседствующих» точек вы- | ||
| + | борки | ||
| + | D | ||
| + | окажется большим, либо равным значе- | ||
| + | нию параметра | ||
| + | MCP | ||
| + | (рис. 1). | ||
| + | Точка Х является прямо достижимой по плот- | ||
| + | ности от точки | ||
| + | f | ||
| + | (при соответствующих и | ||
| + | MCP | ||
| + | ), если точка | ||
| + | XX , т.е. точка Х – это | ||
| + | одна из точек f для другого окружения (соседства), | ||
| + | где f – окруженная точка (рис. 2). | ||
| + | |||
| + | Рис. 1. Окруженная | ||
| + | точка при МСР = 5 | ||
| + | Рис. 2. Точка Х прямо достижима | ||
| + | по плотности от точки f | ||
| + | Достижимость по плотности – это транзитив- | ||
| + | ное замыкание прямо достижимой по плотности | ||
| + | точки. Точка | ||
| + | f | ||
| + | достижима по плотности из точки | ||
| + | X | ||
| + | , но точка | ||
| + | X | ||
| + | не достижима по плотности из точ- | ||
| + | ки | ||
| + | f | ||
| + | (рис. 3). | ||
| + | |||
| + | == Вычислительное ядро алгоритма == | ||
| + | |||
| + | Вычислительным ядром алгоритма является нахождение <math>\varepsilon</math>-соседей каждой точки входного множества <math>X</math>. | ||
| + | |||
| + | Для решения этой задачи требуется найти расстояния между любыми двумя точками множества <math>X</math> по заданной метрике. Например, если используется расстояние Минковского порядка <math>k</math>, то расстояние между точками <math>p=(p_1,...,p_n) \in X</math> и <math>q=(q_1,...,q_n) \in X</math> вычисляется как <math>D(p, q) = (\sum_{i = 1}^{n}|p_i - q_i|^k)^{1 / k}</math>, частным случаем которой при <math>k = 2</math> является широко распространённая евклидова метрика <math>D(p, q) = \sqrt{\sum_{i = 1}^{n} (p_i - q_i)^2}</math>. | ||
| + | |||
| + | == Макроструктура алгоритма == | ||
| + | |||
| + | Как записано и в [[#Вычислительное ядро алгоритма|описании ядра алгоритма]], основную часть метода составляют вызовы функции <math>request\_neighbours</math> получения <math>\varepsilon</math>-соседей и нахождение расстояний между точками множества <math>X</math>. | ||
| + | |||
| + | == Схема реализации последовательного алгоритма == | ||
| + | |||
| + | |||
| + | <math>DBSCAN</math> проходит через все точки множества <math>X</math> и определяет, являются ли они шумом или началом нового кластера. | ||
| + | В последнем случае новому кластеру присваивается уникальный номер и вызывается функция расширения кластера. | ||
| + | |||
| + | <math>DBSCAN(\varepsilon, MinPts)</math> | ||
| + | <math>C = 0</math> | ||
| + | for <math>\forall p \in X</math> | ||
| + | if <math>p</math> is visited then | ||
| + | continue | ||
| + | mark <math>p</math> as visited | ||
| + | <math>neighbours</math> = <math>request\_neighbours(p, \varepsilon)</math> | ||
| + | if <math>| neighbours | < MinPts</math> then | ||
| + | mark <math>p</math> as <math>NOISE</math> | ||
| + | else | ||
| + | <math>C = next\_cluster</math> | ||
| + | <math>expand\_cluster(p, neighbours, C, \varepsilon, MinPts)</math> | ||
| + | |||
| + | <math>expand\_cluster</math> рекурсивно проходит через все точки множества <math>neighbours</math> - соседей точки <math>p</math>, | ||
| + | и определяет, принадлежат ли эти точки тому же кластеру <math>C</math>, тем самым расширяя этот кластер. | ||
| + | |||
| + | <math>expand\_cluster(p, neighbours, C, \varepsilon, MinPts)</math> | ||
| + | add <math>p</math> to cluster <math>C</math> | ||
| + | for <math>\forall p' \in neighbours</math> | ||
| + | if <math>p'</math> is not visited | ||
| + | mark <math>p'</math> as visited | ||
| + | <math>neighbours'</math> = <math>request\_neighbours(p, \varepsilon)</math> | ||
| + | if <math>| neighbours' | \ \ge MinPts</math> | ||
| + | <math>neighbours</math> = <math>neighbours \cup neighbours'</math> | ||
| + | if <math>p'</math> is not yet member of any cluster | ||
| + | add <math>p'</math> to cluster <math>C</math> | ||
| + | |||
| + | <math>request\_neighbours</math> возвращает для точки <math>p</math> множество всех её <math>\varepsilon</math>-соседей, | ||
| + | используя функцию расстояния <math>D</math> | ||
| + | <math>request\_neighbours(p, \varepsilon)</math> | ||
| + | return <math>\{ p' \ | \ \forall p' \in X: D(p, p') < \varepsilon \}</math> | ||
| + | |||
| + | == Последовательная сложность алгоритма == | ||
| + | |||
| + | DBSCAN проходит через каждую точку входного множества, возможно, по несколько раз. Временная сложность зависит в большей степени от вызова функции <math>request\_neighbours</math> (нахождение <math>\varepsilon</math>-соседей для заданной точки). Эта функция вызывается ровно один раз для каждой точки множества <math>X</math>. | ||
| + | |||
| + | Если использовать индексированную структуру данных (например, R-деревья), выполняющую операцию <math>request\_neighbours</math> за <math>O(\log n)</math>, то суммарная сложность алгоритма в среднем составит <math>O(n \log n)</math>, с учётом хорошо подобранного параметра <math>\varepsilon</math>, такого что в среднем <math>request\_neighbours</math> возвращает <math>O(\log n)</math> точек. Без использования ускоряющих структур или на вырожденных данных (таких, что все точки находятся на расстоянии меньшем, чем <math>\varepsilon</math> друг от друга) сложность по времени в худшем случае будет <math>O(n^2)</math>. | ||
| + | |||
| + | |||
| + | Расстояния между точками можно вычислить заранее за <math>O(\frac {n(n - 1)}{2})</math>, например в виде матрицы расстояний, но это потребует <math>O(n^2)</math> памяти. Иначе, расстояния будут вычисляться при каждом запуске функции <math>request\_neighbours</math> за <math>O(n)</math> и потребуют <math>O(n)</math> памяти. Итоговая сложность вычисления расстояний в таком случае составляет <math>O(n^2)</math>. Сложность рассчета расстояний зависит от природы объектов из <math>X</math> и заданной метрики <math>D</math>. Например, если <math>X\subset\mathbb{R}^m</math>, то сложность равна <math>O(m)</math>, но оценка может быть улучшена при использовании векторных операций. | ||
| + | |||
| + | == Информационный граф == | ||
| + | |||
| + | Опишем граф алгоритма<ref>Воеводин В.В. Математические основы параллельных вычислений// М.: Изд. Моск. ун-та, 1991. 345 с.</ref><ref>Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ - Петербург, 2002. – 608 с.</ref><ref>Фролов А.В.. Принципы построения и описание языка Сигма. Препринт ОВМ АН N 236. М.: ОВМ АН СССР, 1989.</ref>. | ||
| + | |||
| + | |||
| + | [[File:Dbscan abstract.png |thumb|right|320px| Рис. 2. Внешний цикл алгоритма.]] | ||
| + | |||
| + | |||
| + | На рис. 2 изображен информационный граф внешнего цикла алгоритма, который соответствует коду основной функции <math>DBSCAN</math>: | ||
| + | *Макрооперация ''Init'' заключается в получении множества <math>X</math> и инициирования вспомогательных структур. | ||
| + | *Макрооперация ''Choose'' производит выбор непосещенной точки из <math>X</math>. | ||
| + | *Макрооперация ''Build cluster'' строит кластер, если точка ядровая, или объявляет ее шумом. | ||
| + | |||
| + | |||
| + | Переход от ''Build cluster'' к ''Choose'' заключает в себе зависимость данных о принадлежности некоторых точек к текущему кластеру или шуму и об их посещенности. | ||
| + | |||
| + | [[File:Expand cluster 2.png |thumb|right|600px| Рис. 3. Расширение кластера.]] | ||
| + | |||
| + | |||
| + | На рис. 3 изображен информационный граф алгоритма расширения кластера из начальной точки кластера: | ||
| + | *Макрооперация ''Init'' заключается в создании кластера из его начальной вершины. | ||
| + | *Макрооперация ''Nε'' вычисляет множество <math>\varepsilon</math>-соседей. | ||
| + | *Желтым цветом обозначены узлы, в которых точки из <math>\varepsilon</math>-соседей классифицируются на ядровые, граничные точки и шум. В рамках операции для конкретного соседа вычисляется множество его <math>\varepsilon</math>-соседей. | ||
| + | *Макрооперации ''Ñε'', ''Ňε'', ... производят объединение входных множеств. | ||
| + | *Макрооперация ''Ø'' выполняется тогда, когда объединение входных множеств является пустым. | ||
| + | |||
| + | |||
| + | [[File:N eps 3.png |thumb|right|320px| Рис. 4. Подсчет <math>\varepsilon</math>-соседей.]] | ||
| + | |||
| + | На рис. 4 изображен информационный граф алгоритма вычисления множества <math>\varepsilon</math>-соседей: | ||
| + | *Операция ''D'' - вычисление расстояния между точками. | ||
| + | *Операция ''ε'' - сравнение расстояния с ε. | ||
| + | *Операция ''U'' - объединение результатов. | ||
| + | |||
| + | == Ресурс параллелизма алгоритма == | ||
| + | |||
| + | Поиск <math>\varepsilon</math>-соседей требует вычисления <math>n</math> расстояний (функция <math>D</math>) и выполнения <math>n</math> сравнений с <math>\varepsilon</math>. Эти операции для каждой пары точек независимы и могут быть выполнены параллельно. Таким образом, при наличии неограниченного числа процессоров сложность поиска составит <math>O(1)</math>. Т.к. поиск выполняется для каждой точки ровно один раз, параллельная сложность всего алгоритма составит <math>O(n)</math>. | ||
| + | |||
| + | == Входные и выходные данные алгоритма == | ||
| + | |||
| + | |||
| + | Вход алгоритма: множество точек X из n-мерного пространства, на котором определена функция расстояния D. В наиболее распространенном случае пространственной кластеризации используется Евлидово расстояние между векторами из <math>\mathbb{R}^n</math>. | ||
| + | |||
| + | Выход алгоритма: размеченное множество точек <math>X</math>, в котором каждой точке соответствует номер ее кластера. Обычно каждой точке из <math>X</math> сопоставляется ее номер, а на выходе алгоритм дает отображение номеров точек в номера соответствующих им кластеров, например в виде вектора размера <math>|X|</math>. | ||
| + | |||
| + | == Свойства алгоритма == | ||
| + | |||
| + | Соотношение последовательной и параллельной сложностей алгоритма является линейным (отношение квадратичной к линейной). | ||
| + | |||
| + | При этом вычислительная мощность, как отношение числа операций к суммарному объему входных и выходных данных линейна. | ||
| + | |||
| + | === Преимущества алгоритма === | ||
| + | |||
| + | # не требует указывать число кластеров; | ||
| + | # может определять кластера произвольной формы; | ||
| + | # может определять шум и устойчив к выбросам; | ||
| + | # требует всего два параметра и по в большинстве случаев не чувствителен к порядку заданных точек; | ||
| + | # параллельная реализация сбалансирована по количеству и виду производимых операций (вычисление расстояния, сравнение с <math>\varepsilon</math>). | ||
| + | |||
| + | === Недостатки алгоритма === | ||
| + | |||
| + | # не детерминирован: граничные точки, достижимые из более, чем одного кластера, могут быть частью любого из них в зависимости от порядка обрабатываемых данных. Однако такая ситуация возникает редко, а относительно ядровых точек и шума DBSCAN детерминирован. Впрочем, от недетерминизма можно избавиться, если считать все граничные точки шумом (алгоритм DBSCAN*); | ||
| + | # качество алгоритма зависит от используемой функции расстояния <math>D</math>. Наиболее часто используемое Евклидово расстояние в многомерных множествах может оказаться практически бесполезным из-за так называемого "проклятия размерности", значительно затрудняя нахождение подходящего значения <math>\varepsilon</math>; | ||
| + | # не может выделять кластеры, имеющие разную плотность, так как параметры алгоритма не могут быть выбранны отдельно для каждого кластера. | ||
| + | |||
| + | = Программная реализация алгоритма = | ||
| + | |||
| + | == Особенности реализации последовательного алгоритма == | ||
| + | |||
| + | == Локальность данных и вычислений == | ||
| + | |||
| + | == Возможные способы и особенности параллельной реализации алгоритма == | ||
| + | |||
| + | == Масштабируемость алгоритма и его реализации == | ||
| + | |||
| + | !!! ЭКСПЕРИМЕНТЫ ДО 15 НОЯБРЯ !!! | ||
| + | |||
| + | == Динамические характеристики и эффективность реализации алгоритма == | ||
| + | |||
| + | == Выводы для классов архитектур == | ||
| + | |||
| + | == Существующие реализации алгоритма == | ||
| + | |||
| + | * [http://scikit-learn.org/stable/modules/generated/sklearn.cluster.DBSCAN.html Scikit learn (Python)] | ||
| + | * [https://cran.r-project.org/web/packages/dbscan/dbscan.pdf R-project] ([https://github.com/mhahsler/dbscan github]) | ||
| + | * [https://www.mathworks.com/matlabcentral/fileexchange/52905-dbscan-clustering-algorithm Matlab] | ||
| + | * P-DBSCAN (Parallel DBSCAN)<ref>Chen, Min, Xuedong Gao, and HuiFei Li. "Parallel DBSCAN with priority r-tree." Information Management and Engineering (ICIME), 2010 The 2nd IEEE International Conference on. IEEE, 2010.</ref> | ||
| + | * Parallel DBSCAN with MPI<ref>Savvas, Ilias K., and Dimitrios Tselios. "Parallelizing DBSCaN Algorithm Using MPI." Enabling Technologies: Infrastructure for Collaborative Enterprises (WETICE), 2016 IEEE 25th International Conference on. IEEE, 2016.</ref> | ||
| + | * PDSDBSCAN (Parallel Disjoint-Set DBSCAN)<ref>Patwary, Md Mostofa Ali, et al. "A new scalable parallel DBSCAN algorithm using the disjoint-set data structure." High Performance Computing, Networking, Storage and Analysis (SC), 2012 International Conference for. IEEE, 2012.</ref> | ||
| + | |||
| + | = Литература = | ||
| + | |||
| + | <references /> | ||
Версия 05:52, 20 января 2017
Авторы описания: Титов Д.Е.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Под кластеризацией понимается деление заданного множества точек данных (объектов) на подгруппы, каждая из которых, насколько это возможно, однородна. В основе метода кластеризации DBSCAN лежит объединение некоторых объектов в соответствии с их внутригрупповым «соединением». Для проведения корректной процедуры кластеризации необходимо указать критерии, по которым объекты будут объединены в кластеры. Прежде всего, необходимо сказать, что кластеры представляют собой плотные области некоторых объектов в пространстве данных, разделенных между собой объектами, плотность которых значительно ниже. Расположение точек в одном кластере обусловлено их соединением, т.е. некоторой связью между собой.
1.2 Математическое описание алгоритма
Плотность точек для данной точки [math]X[/math] определяется двумя параметрами. Первым из них является [math]\varepsilon[/math] – радиус «соседства» (приближенности) точки [math]X[/math]. Тогда множество [math]M(X)[/math] будет включать в себя такие точки n,1i,f i , для которых следующее не- равенство будет истинно n,1i,f,Xdist i . (1). Функция )2var,1(vardist
определяет расстоя-
ние между объектами выборки D . Это расстояние может вычисляться различными способами, например, как евклидово расстояние или с помо- щью метрики Минковского. Вторым параметром определения плотности точек является MCP – это минимальное количество точек, которые расположены ближе всего к данной точке согласно определенному радиусу . Точка n,1i,f i
будет являться окруженной
точкой (согласно и MCP ) если MCPX . (2) Это значит, что точка n,1i,f i
окружен-
ная, если количество «соседствующих» точек вы- борки D
окажется большим, либо равным значе-
нию параметра MCP
(рис. 1).
Точка Х является прямо достижимой по плот- ности от точки f
(при соответствующих и
MCP ), если точка XX , т.е. точка Х – это одна из точек f для другого окружения (соседства), где f – окруженная точка (рис. 2).
Рис. 1. Окруженная точка при МСР = 5 Рис. 2. Точка Х прямо достижима по плотности от точки f Достижимость по плотности – это транзитив- ное замыкание прямо достижимой по плотности точки. Точка f
достижима по плотности из точки
X , но точка X
не достижима по плотности из точ-
ки f
(рис. 3).
1.3 Вычислительное ядро алгоритма
Вычислительным ядром алгоритма является нахождение [math]\varepsilon[/math]-соседей каждой точки входного множества [math]X[/math].
Для решения этой задачи требуется найти расстояния между любыми двумя точками множества [math]X[/math] по заданной метрике. Например, если используется расстояние Минковского порядка [math]k[/math], то расстояние между точками [math]p=(p_1,...,p_n) \in X[/math] и [math]q=(q_1,...,q_n) \in X[/math] вычисляется как [math]D(p, q) = (\sum_{i = 1}^{n}|p_i - q_i|^k)^{1 / k}[/math], частным случаем которой при [math]k = 2[/math] является широко распространённая евклидова метрика [math]D(p, q) = \sqrt{\sum_{i = 1}^{n} (p_i - q_i)^2}[/math].
1.4 Макроструктура алгоритма
Как записано и в описании ядра алгоритма, основную часть метода составляют вызовы функции [math]request\_neighbours[/math] получения [math]\varepsilon[/math]-соседей и нахождение расстояний между точками множества [math]X[/math].
1.5 Схема реализации последовательного алгоритма
[math]DBSCAN[/math] проходит через все точки множества [math]X[/math] и определяет, являются ли они шумом или началом нового кластера. В последнем случае новому кластеру присваивается уникальный номер и вызывается функция расширения кластера.
[math]DBSCAN(\varepsilon, MinPts)[/math] [math]C = 0[/math] for [math]\forall p \in X[/math] if [math]p[/math] is visited then continue mark [math]p[/math] as visited [math]neighbours[/math] = [math]request\_neighbours(p, \varepsilon)[/math] if [math]| neighbours | \lt MinPts[/math] then mark [math]p[/math] as [math]NOISE[/math] else [math]C = next\_cluster[/math] [math]expand\_cluster(p, neighbours, C, \varepsilon, MinPts)[/math]
[math]expand\_cluster[/math] рекурсивно проходит через все точки множества [math]neighbours[/math] - соседей точки [math]p[/math], и определяет, принадлежат ли эти точки тому же кластеру [math]C[/math], тем самым расширяя этот кластер.
[math]expand\_cluster(p, neighbours, C, \varepsilon, MinPts)[/math] add [math]p[/math] to cluster [math]C[/math] for [math]\forall p' \in neighbours[/math] if [math]p'[/math] is not visited mark [math]p'[/math] as visited [math]neighbours'[/math] = [math]request\_neighbours(p, \varepsilon)[/math] if [math]| neighbours' | \ \ge MinPts[/math] [math]neighbours[/math] = [math]neighbours \cup neighbours'[/math] if [math]p'[/math] is not yet member of any cluster add [math]p'[/math] to cluster [math]C[/math]
[math]request\_neighbours[/math] возвращает для точки [math]p[/math] множество всех её [math]\varepsilon[/math]-соседей, используя функцию расстояния [math]D[/math]
[math]request\_neighbours(p, \varepsilon)[/math] return [math]\{ p' \ | \ \forall p' \in X: D(p, p') \lt \varepsilon \}[/math]
1.6 Последовательная сложность алгоритма
DBSCAN проходит через каждую точку входного множества, возможно, по несколько раз. Временная сложность зависит в большей степени от вызова функции [math]request\_neighbours[/math] (нахождение [math]\varepsilon[/math]-соседей для заданной точки). Эта функция вызывается ровно один раз для каждой точки множества [math]X[/math].
Если использовать индексированную структуру данных (например, R-деревья), выполняющую операцию [math]request\_neighbours[/math] за [math]O(\log n)[/math], то суммарная сложность алгоритма в среднем составит [math]O(n \log n)[/math], с учётом хорошо подобранного параметра [math]\varepsilon[/math], такого что в среднем [math]request\_neighbours[/math] возвращает [math]O(\log n)[/math] точек. Без использования ускоряющих структур или на вырожденных данных (таких, что все точки находятся на расстоянии меньшем, чем [math]\varepsilon[/math] друг от друга) сложность по времени в худшем случае будет [math]O(n^2)[/math].
Расстояния между точками можно вычислить заранее за [math]O(\frac {n(n - 1)}{2})[/math], например в виде матрицы расстояний, но это потребует [math]O(n^2)[/math] памяти. Иначе, расстояния будут вычисляться при каждом запуске функции [math]request\_neighbours[/math] за [math]O(n)[/math] и потребуют [math]O(n)[/math] памяти. Итоговая сложность вычисления расстояний в таком случае составляет [math]O(n^2)[/math]. Сложность рассчета расстояний зависит от природы объектов из [math]X[/math] и заданной метрики [math]D[/math]. Например, если [math]X\subset\mathbb{R}^m[/math], то сложность равна [math]O(m)[/math], но оценка может быть улучшена при использовании векторных операций.
1.7 Информационный граф
Опишем граф алгоритма[1][2][3].
На рис. 2 изображен информационный граф внешнего цикла алгоритма, который соответствует коду основной функции [math]DBSCAN[/math]:
- Макрооперация Init заключается в получении множества [math]X[/math] и инициирования вспомогательных структур.
- Макрооперация Choose производит выбор непосещенной точки из [math]X[/math].
- Макрооперация Build cluster строит кластер, если точка ядровая, или объявляет ее шумом.
Переход от Build cluster к Choose заключает в себе зависимость данных о принадлежности некоторых точек к текущему кластеру или шуму и об их посещенности.
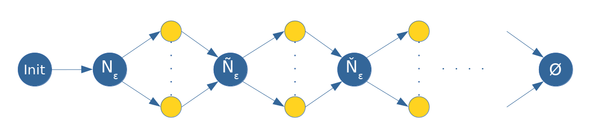
На рис. 3 изображен информационный граф алгоритма расширения кластера из начальной точки кластера:
- Макрооперация Init заключается в создании кластера из его начальной вершины.
- Макрооперация Nε вычисляет множество [math]\varepsilon[/math]-соседей.
- Желтым цветом обозначены узлы, в которых точки из [math]\varepsilon[/math]-соседей классифицируются на ядровые, граничные точки и шум. В рамках операции для конкретного соседа вычисляется множество его [math]\varepsilon[/math]-соседей.
- Макрооперации Ñε, Ňε, ... производят объединение входных множеств.
- Макрооперация Ø выполняется тогда, когда объединение входных множеств является пустым.
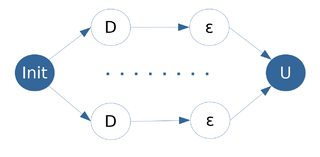
На рис. 4 изображен информационный граф алгоритма вычисления множества [math]\varepsilon[/math]-соседей:
- Операция D - вычисление расстояния между точками.
- Операция ε - сравнение расстояния с ε.
- Операция U - объединение результатов.
1.8 Ресурс параллелизма алгоритма
Поиск [math]\varepsilon[/math]-соседей требует вычисления [math]n[/math] расстояний (функция [math]D[/math]) и выполнения [math]n[/math] сравнений с [math]\varepsilon[/math]. Эти операции для каждой пары точек независимы и могут быть выполнены параллельно. Таким образом, при наличии неограниченного числа процессоров сложность поиска составит [math]O(1)[/math]. Т.к. поиск выполняется для каждой точки ровно один раз, параллельная сложность всего алгоритма составит [math]O(n)[/math].
1.9 Входные и выходные данные алгоритма
Вход алгоритма: множество точек X из n-мерного пространства, на котором определена функция расстояния D. В наиболее распространенном случае пространственной кластеризации используется Евлидово расстояние между векторами из [math]\mathbb{R}^n[/math].
Выход алгоритма: размеченное множество точек [math]X[/math], в котором каждой точке соответствует номер ее кластера. Обычно каждой точке из [math]X[/math] сопоставляется ее номер, а на выходе алгоритм дает отображение номеров точек в номера соответствующих им кластеров, например в виде вектора размера [math]|X|[/math].
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложностей алгоритма является линейным (отношение квадратичной к линейной).
При этом вычислительная мощность, как отношение числа операций к суммарному объему входных и выходных данных линейна.
1.10.1 Преимущества алгоритма
- не требует указывать число кластеров;
- может определять кластера произвольной формы;
- может определять шум и устойчив к выбросам;
- требует всего два параметра и по в большинстве случаев не чувствителен к порядку заданных точек;
- параллельная реализация сбалансирована по количеству и виду производимых операций (вычисление расстояния, сравнение с [math]\varepsilon[/math]).
1.10.2 Недостатки алгоритма
- не детерминирован: граничные точки, достижимые из более, чем одного кластера, могут быть частью любого из них в зависимости от порядка обрабатываемых данных. Однако такая ситуация возникает редко, а относительно ядровых точек и шума DBSCAN детерминирован. Впрочем, от недетерминизма можно избавиться, если считать все граничные точки шумом (алгоритм DBSCAN*);
- качество алгоритма зависит от используемой функции расстояния [math]D[/math]. Наиболее часто используемое Евклидово расстояние в многомерных множествах может оказаться практически бесполезным из-за так называемого "проклятия размерности", значительно затрудняя нахождение подходящего значения [math]\varepsilon[/math];
- не может выделять кластеры, имеющие разную плотность, так как параметры алгоритма не могут быть выбранны отдельно для каждого кластера.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
!!! ЭКСПЕРИМЕНТЫ ДО 15 НОЯБРЯ !!!
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
- Scikit learn (Python)
- R-project (github)
- Matlab
- P-DBSCAN (Parallel DBSCAN)[4]
- Parallel DBSCAN with MPI[5]
- PDSDBSCAN (Parallel Disjoint-Set DBSCAN)[6]
3 Литература
- ↑ Воеводин В.В. Математические основы параллельных вычислений// М.: Изд. Моск. ун-та, 1991. 345 с.
- ↑ Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ - Петербург, 2002. – 608 с.
- ↑ Фролов А.В.. Принципы построения и описание языка Сигма. Препринт ОВМ АН N 236. М.: ОВМ АН СССР, 1989.
- ↑ Chen, Min, Xuedong Gao, and HuiFei Li. "Parallel DBSCAN with priority r-tree." Information Management and Engineering (ICIME), 2010 The 2nd IEEE International Conference on. IEEE, 2010.
- ↑ Savvas, Ilias K., and Dimitrios Tselios. "Parallelizing DBSCaN Algorithm Using MPI." Enabling Technologies: Infrastructure for Collaborative Enterprises (WETICE), 2016 IEEE 25th International Conference on. IEEE, 2016.
- ↑ Patwary, Md Mostofa Ali, et al. "A new scalable parallel DBSCAN algorithm using the disjoint-set data structure." High Performance Computing, Networking, Storage and Analysis (SC), 2012 International Conference for. IEEE, 2012.