VladimirDobrovolsky611/Алгоритм SDDP: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
| Строка 8: | Строка 8: | ||
== Математическое описание алгоритма== | == Математическое описание алгоритма== | ||
Исходные данные: | Исходные данные: | ||
| − | + | 1. Количество этапов T, количество состояний на каждом этапе <math>m_t</math>, <math>t = 1,...,T</math> | |
| − | + | ||
| − | + | 2. Размерность задачи N (размерность управляющего правила) | |
| − | + | ||
| + | 3. Вероятности переходов <math>p_{nt}; t = 1,...,T; n = 1,...,m_t</math> | ||
| + | |||
| + | 4. матрицы и векторы, характеризующие каждое состояние системы <math> \xi_i^t=(A_i^t, \ B_i^t, \ b_i^t, \ c_i^t) </math> | ||
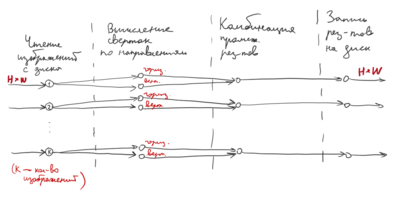
Совокупность входных параметров в пунктах 1 - 4 формируют сценарную решетку задачи (см. рис. 1) | Совокупность входных параметров в пунктах 1 - 4 формируют сценарную решетку задачи (см. рис. 1) | ||
Считается, что на 1-м этапе задача детерминирована. Здесь присутствует всего одно состояние <math> \xi_1 =(A_1, \ b_1, \ c_1) </math>. | Считается, что на 1-м этапе задача детерминирована. Здесь присутствует всего одно состояние <math> \xi_1 =(A_1, \ b_1, \ c_1) </math>. | ||
Версия 15:15, 6 февраля 2017
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Стохастическое двойственное динамическое программирование (SDDP) – это метод оптимизации, предназначенный для решения динамических задач в условиях неопределенности, то есть в случае, когда некоторые параметры задачи не являются детерминированными. В силу фундаментальности постановки задачи, данный алгоритм может быть применен в самых различных прикладных областях. Например, на сегодняшний день, стохастическое двойственное динамическое программирование активно используется для управления ГЭС в Норвегии, а также вводится в банках для управления рыночными рисками. На сегодняшний день также широко распространены альтернативные динамические методы поиска решений в условиях неопределенности, например, методы, работающие на принципах построения дерева возможных исходов, или методы, работающие на принципах управляющих правил. Однако, методы, работающие по принципу построения дерева, неизбежно сталкиваются с широко известным «проклятием размерности» (curse of dimensionality), а методы, построенные на принципах управляющих правил, как правило, требуют серьезные ограничения на тип управляющих правил, а также на свойства стохастических параметров задачи. Также, в задачах динамического управления присутствует проблема тайм-консистентности решения (time-consistence solution).
Алгоритм SDDP (Stochastic dual dynamic programming) впервые был предложен в статье M.V.F. Pereira и L.M.V.G. Pinto "Multi-stage stochastic optimization applied to energy planning" в 1991 году. Далее алгоритм претерпел множество модернизаций и спецификаций, описанных в труде Alexander Shapiro, Darinka Dentcheva, Andrzej Ruszczynski "Lectures on Stochastic Programming: Modeling and Theory", Теперь под аббревиатурой SDDP подразумевается целое семейство алгоритмов.
1.2 Математическое описание алгоритма
Исходные данные: 1. Количество этапов T, количество состояний на каждом этапе [math]m_t[/math], [math]t = 1,...,T[/math]
2. Размерность задачи N (размерность управляющего правила)
3. Вероятности переходов [math]p_{nt}; t = 1,...,T; n = 1,...,m_t[/math]
4. матрицы и векторы, характеризующие каждое состояние системы [math] \xi_i^t=(A_i^t, \ B_i^t, \ b_i^t, \ c_i^t) [/math] Совокупность входных параметров в пунктах 1 - 4 формируют сценарную решетку задачи (см. рис. 1) Считается, что на 1-м этапе задача детерминирована. Здесь присутствует всего одно состояние [math] \xi_1 =(A_1, \ b_1, \ c_1) [/math].
Вычисляемые данные: Матрица управляющих действий [math]X[/math] (элементы [math]x_{it}; \ t \in 1,...,T; \ i \in 1,...,N[/math] - управления для i-го элемента на шаге t)
Постановка задачи:
[math] \left\{\begin{matrix} min \ c_1x_1 + \sum_{i=1}^{m_2}p_{1i}^1Q_2(x_1,\xi_i^2) \\subject \ to \\A_1x_1\geqslant b_1 \\x_1 \geqslant 0 \end{matrix}\right.[/math]
где
[math] Q_t(x_{t-1},\xi_i^t) = \left\{\begin{matrix} min \ c_t^ix_t + \sum_{j=1}^{m_{t+1}}p_{ji}^tQ_{t+1}(x_t,\xi_j^{t+1}) \\subject \ to \\A_t^ix_t + B_t^ix_{t-1}\geqslant b_t^i \\x_t \geqslant 0 \end{matrix}\right. t=2,...,T-1 [/math]
...
[math]
Q_T(x_{T-1},\xi_i^T) =
\left\{\begin{matrix}
min \ c_T^ix_T
\\subject \ to
\\A_T^ix_T + B_T^ix_{T-1}\geqslant b_T^i
\\x_t \geqslant 0
\end{matrix}\right.
[/math]