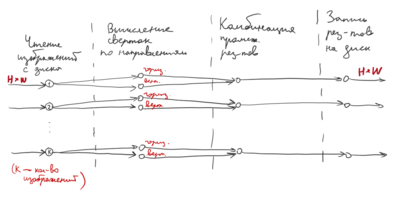
VladimirDobrovolsky611/Алгоритм SDDP: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
| Строка 272: | Строка 272: | ||
Обозначим основные свойства данных задач и Симплекс метода: | Обозначим основные свойства данных задач и Симплекс метода: | ||
| − | Пусть <math> M</math> - количество ограничений, <math>N | + | Пусть <math> M</math> - количество ограничений, <math>N</math> - количество переменных задачи линейного программирования. Тогда: |
1. Практика показывает, что в среднем вычислительная сложность алгоритма составляет <math> M^3 </math> операций | 1. Практика показывает, что в среднем вычислительная сложность алгоритма составляет <math> M^3 </math> операций | ||
Версия 19:38, 6 февраля 2017
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Стохастическое двойственное динамическое программирование (SDDP) – это метод оптимизации, предназначенный для решения динамических задач в условиях неопределенности, то есть в случае, когда некоторые параметры задачи не являются детерминированными. В силу фундаментальности постановки задачи, данный алгоритм может быть применен в самых различных прикладных областях. Например, на сегодняшний день, стохастическое двойственное динамическое программирование активно используется для управления ГЭС в Норвегии, а также вводится в банках для управления рыночными рисками. На сегодняшний день также широко распространены альтернативные динамические методы поиска решений в условиях неопределенности, например, методы, работающие на принципах построения дерева возможных исходов, или методы, работающие на принципах управляющих правил. Однако, методы, работающие по принципу построения дерева, неизбежно сталкиваются с широко известным «проклятием размерности» (curse of dimensionality), а методы, построенные на принципах управляющих правил, как правило, требуют серьезные ограничения на тип управляющих правил, а также на свойства стохастических параметров задачи. Также, в задачах динамического управления присутствует проблема тайм-консистентности решения (time-consistence solution).
Алгоритм SDDP (Stochastic dual dynamic programming) впервые был предложен в статье M.V.F. Pereira и L.M.V.G. Pinto "Multi-stage stochastic optimization applied to energy planning" в 1991 году. Далее алгоритм претерпел множество модернизаций и спецификаций, описанных в труде Alexander Shapiro, Darinka Dentcheva, Andrzej Ruszczynski "Lectures on Stochastic Programming: Modeling and Theory", Теперь под аббревиатурой SDDP подразумевается целое семейство алгоритмов.
1.2 Математическое описание алгоритма
1.2.1 Постановка задачи
Исходные данные:
1. Количество этапов T, количество состояний на каждом этапе [math]m_t[/math], [math]t = 1,...,T[/math]
2. Размерность задачи N (размерность управляющего правила)
3. Вероятности переходов [math]p_{nt}; t = 1,...,T; n = 1,...,m_t[/math]
4. матрицы и векторы, характеризующие каждое состояние системы [math] \xi_i^t=(A_i^t, \ B_i^t, \ b_i^t, \ c_i^t) [/math]
Совокупность входных параметров в пунктах 1 - 4 формируют сценарную решетку задачи (см. рис. 1)
Считается, что на 1-м этапе задача детерминирована. Здесь присутствует всего одно состояние [math] \xi_1 =(A_1, \ b_1, \ c_1) [/math].
Вычисляемые данные:
Матрица управляющих действий [math]X[/math] (элементы [math]x_{it}; \ t \in 1,...,T; \ i \in 1,...,N[/math] - управления для i-го элемента на шаге t)
Постановка задачи:
[math] \left\{\begin{matrix} min \ c_1x_1 + \sum_{i=1}^{m_2}p_{1i}^1Q_2(x_1,\xi_i^2) \\subject \ to \\A_1x_1\geqslant b_1 \\x_1 \geqslant 0 \end{matrix}\right. \ \ \ (1)[/math]
где
[math] Q_t(x_{t-1},\xi_i^t) = \left\{\begin{matrix} min \ c_t^ix_t + \sum_{j=1}^{m_{t+1}}p_{ji}^tQ_{t+1}(x_t,\xi_j^{t+1}) \\subject \ to \\A_t^ix_t + B_t^ix_{t-1}\geqslant b_t^i \\x_t \geqslant 0 \end{matrix}\right. t=2,...,T-1 \ \ \ (2) [/math]
...
[math] Q_T(x_{T-1},\xi_i^T) = \left\{\begin{matrix} min \ c_T^ix_T \\subject \ to \\A_T^ix_T + B_T^ix_{T-1}\geqslant b_T^i \\x_t \geqslant 0 \end{matrix}\right. (3) [/math]
При этом функцию [math]Q_t(x_{t-1},\xi_i^t)[/math] называют функцией будущего спроса (cost-to-go function).
Данная постановка задачи позволяет решать задачи стохастического программирования, где в качестве метрики взято мат. ожидание по состояниям системы. Существуют также и другие расширения данного алгоритма, где в качестве метрики взято значение Value at Risk или Expected Shortfall, широко используемые в оценки рисков финансовых потерь.
1.2.2 Прикладная область
Существует множество прикладных задач, для которых используется данный алгоритм. далее приведены некоторые примеры:
1. Управление ГЭС
Моделируется следующая ситуация:
Существует водохранилище с ограниченным объемом воды. водохранилище наполняется за счет осадков, а опустошается с помощью шлюзов ГЭС. Также существует населенный пункт, потребляющий электроэнергию. ГЭС может генерировать электричество 2-мя способами: спускать воду из водохранилища или использовать топливные генераторы. Себестоимость электроэнергия, полученная ГЭС за счет спуска воды можно считать нулевой, в то время, как электроэнергия, выработанная за счет топливных генераторов имеет значительную себестоимость.
Считается, что количество энергии, потребляемой населенным пунктом, а также объем осадков - случайные процессы, распределения которых можно получить с помощью исторических данных. Объем водохранилища и себестоимость производства электричества тем или иным способом - известны и фиксированы. В данных условиях стоит задача минимизировать финансовые потери ГЭС на несколько лет вперед.
2. Управление портфелем ценных бумаг.
Инвестор обладает некоторым стартовым капиталом, который можно инвестировать в заданный набор ценных бумаг. Инвестор формирует финансовый портфель на несколько лет, но внутри данного периода возможны ребалансировки портфеля, проводимые, однако, без вывода и без привлечения дополнительных средств. Прирост цен активов портфеля, а также величина дивидендных выплат - случайны. При этом, транзакционные издержки, начальный капитал инвестора, а также набор возможных активов для вложения - фиксированные величины. В данных условиях стоит задача минимизировать финансовые потери инвестора.
1.2.3 Алгоритм решения
Алгоритм решения задачи (1) - (3) опирается на фундаментальное утверждение:
cost-to-go function, опсанная уравнением (2) является кусочно-линейной относительно аргумента [math]x_{t-1}[/math]
Данное утверждение позволяет сделать вывод, что задача (1) - (3) может быть сведена к задаче линейного программирования.
В ходе доказательства данного утверждения также показывается, что в задачу можно решить итерационно, причем каждую итерацию можно разбить на 3 этапа:
1. Инициализаци
2. Обратный ход
3. Прямой ход
На каждой итерации,в ходе прямого хода задачи достигается верхняя оценка решения, а в ходе обратного - нижняя. Причем при устремлении количества итераций к бесконечности, данные оценки сходятся к истинному решению.
1.2.3.1 Инициализация.
На данном этапе генерируются случайные сценарии на сценарной решетки задачи. Количество инициализируемых случайных сценариев может варьироваться в зависимости от структуры сетки. До сих пор не исследовано оптимальное с точки зрения скорости выполнения количество пробных сценариев и зависимость выбора этого количества от размерности решетки. Будем считать, что на каждой итерации формируется [math]K[/math] случайных сценариев, которые представляют из себя наборы состояний [math](\widehat{\xi}_{1}^{i_k},...,\widehat{\xi}_{T}^{i_k}) \ k = 1,...,K[/math]
Для каждого пробного сценария на каждом шаге решается прямая задача линейного программирования:
[math] Q_t^{i_k}(\widehat{x}_{t-1}^{k},\widehat{\xi}_{t}^{i_k}) = \left\{\begin{matrix} min \ c_t^{i_k}x_t \\ subject \ to \\ A_t^{i_k}x_t + B_t^{i_k}\widehat{x}_{t-1}^k\geq b_t^{i_k} \end{matrix}\right. \ \ \ (2) [/math]
Получается [math]K[/math] пробных решений:
[math] \widehat{x}_t^k = \left\{\begin{matrix} argmin \ c_t^{i_k}x_t \\ subject \ to \\ A_t^{i_k}x_t + B_t^{i_k}\widehat{x}_{t-1}^k\geq b_t^{i_k} \end{matrix}\right. [/math]
[math]k = 1,...,K[/math]
1.2.3.2 Обратный ход
На обратном ходе с помощью каждого пробного решения формируется отсекающая гиперплоскость, ограничивающая решение снизу.
Уравнение гиперплоскости получается в ходе решения прямой и обратной задач линейного программирования:
На шаге [math]T[/math]:
Прямые задачи:
[math] Q_T(\widehat{x}_{T-1}^k,\xi_T^i) = \left\{\begin{matrix} min \ c_T^{i_k}x_T \\ subject \ to \\ A_T^{i_k}x_T + B_T^{i_k}\widehat{x}_{T-1}\geq b_T^{i_k} \end{matrix}\right. (4) [/math]
Двойственные задачи:
[math] Q_T(\widehat{x}_{T-1}^k,\xi_T^i) = \left\{\begin{matrix} max \ \pi_T^{i_k}(b_t^i - B_T^i\widehat{x}_{T-1}^{i_k}) \\ subject \ to \\ \pi_T^{i_k}A_T^{i_k}\leq c_T^{i_k} \end{matrix}\right. (5) [/math]
Уравнение отсекающей гиперплоскости:
[math] l_T^k(x_{T-1}^k) = \sum_{j=1}^{m_T} \ p_{Tj}c_T^jx_t^{i_kj}+ (-\sum_{j=1}^{m_T}p_{tj}\pi_t^{i_kj}B_t^j)(x_{T-1}^{i_k} - \widehat{x}_{T-1}^{i_k}) \ \ (6) [/math]
На этапах [math]t = 1,...,T-1[/math]:
Прямые задачи:
[math] Q_t(x_{t-1}^k,\xi_t^i) = \left\{\begin{matrix} min \ c_t^{i_k}x_t + \gamma_t \\ subject \ to \\ A_t^{i_k}x_t + B_t^{i_k}\widehat{x}_{t-1}\geq b_t^{i_k} \\ \gamma_t\geq l_{t+1}(x_t^{i_k}) \end{matrix}\right. (7) [/math]
Двойственные задачи:
[math] Q_t(\widehat{x}_{t-1}^k,\xi_t^i) = \left\{\begin{matrix} max \ \pi_T^{i_k}(\widetilde{b}_t^i - \widetilde{B}_t^i\widehat{x}_{t-1}^{i_k}) \\ subject \ to \\ \pi_t^{i_k}\widetilde{A}_t^{i_k}\leq \widetilde{c}_t^{i_k} \end{matrix}\right. (8) [/math]
Уравнение отсекающей гиперплоскости:
[math] l_t^k(x_{t-1}^k) = \sum_{j=1}^{m_t} \ p_{tj}\widetilde{c}_t^jx_t^{i_kj}+ (-\sum_{j=1}^{m_t}p_{tj}\pi_t^{i_kj}\widetilde{B}_t^j)(x_{t-1}^{i_k} - \widehat{x}_{t-1}^{i_k}) \ \ (9) [/math]
В результате, значение функционала при оптимальном решении в уравнении (7) является нижней оценкой решения [math]\underline{s}[/math]
1.2.3.3 Прямой ход
На прямом ходе алгоритма производятся те же действия, что и при инициализации, однако при решении прямых задач линейного программирования дополнительными ограничениями выступают отсекающие гиперплоскости, полученные на обратном ходе алгоритма.
На прямом ходе алгоритма генерируются пробные сценарии [math]\widehat{\xi}_t^k; \ k = 1,...,K[/math]
Для каждого из K сценариев решаются задачи (7), в результате получается верхняя оценка [math]\overline{s}[/math]
Если [math]|\overline{s} - \underline{s}| \leq \varepsilon[/math] то решение найдено. Иначе, переход на следующую итерацию.
1.3 Вычислительное ядро алгоритма
С вычислительной точки зрения, алгоритм SDDP является композицией большого количества вычислений задач линейного программирования сравнительно небольших размерностей. С точки зрения компьютерной реализации, алгоритм состоит из двух фаз: 1. Вычисление прямой или двойственной задачи линейного программирования. Получения значения функционала и оптимального решения 2. Запись в пространство гиперплоскостей коэффициентов задачи. Следует отметить, что при каждой новой итерации, пространство гиперплоскостей пополняется новыми отсекающими гиперплоскостями, полученными посредством решения более приближенных задач, чем на предыдущих итерациях. Поэтому, размерность задач линейного программирования растет(т.к. растет количество ограничений) в то время, как эффективность данных задач не увеличивается. Для этого был введен также алгоритм по удалению ненужных отсекающих гиперплоскостей.
1.4 Макроструктура алгоритма
Алгоритм SDDP является композицией задач линейного программирования. Пусть выполнены следующие условия:
[math]x = (x_1,...,x_N);[/math]
[math]\pi = (\pi_1,...,\pi_M);[/math]
[math]A \in R^{N \ X \ M};[/math]
[math]c \in R^N;\lt math\gt [/math]
Тогда, задачей линейного программирования называется задача следующего вида:
[math] \left\{\begin{matrix} min \ c^Tx \\ subject to \\ Ax \geq b \\ x_i \geq 0; \ i = 1,...,N \end{matrix}\right. (10) [/math]
Двойственной задачей к задаче (10) является задача следующего вида:
[math] \left\{\begin{matrix} max \ \pi^Tb \\ subject to \\ \pi^TA \leq c \\ \pi_i \geq 0; \ i = 1,...,M \end{matrix}\right. (11) [/math]
Задача (10) и задача (11) могут быть решены Симплекс методом
Обозначим основные свойства данных задач и Симплекс метода:
Пусть [math] M[/math] - количество ограничений, [math]N[/math] - количество переменных задачи линейного программирования. Тогда:
1. Практика показывает, что в среднем вычислительная сложность алгоритма составляет [math] M^3 [/math] операций
2. Количество итераций знаключение между [math] M [/math]и [math]2M [/math]
3. В худшем случае ввиду комбинаторных особенностей алгоритма, симплекс метод имеет экспоненциальную сложность, однако в среднем, задача решается с полиноминальной сложностью.
4. Количество ограничений влияет на время выполнения метода гораздо сильнее, чем количество переменных
5. Оптимальное значение функционала задачи (10) совпадает с оптимальным значением функционала (11)
6. Для решения алгоритма SDDP использовался готовый солвер для решения задач линейного программирования - lpSolve