Участник:Bormas: различия между версиями
Bormas (обсуждение | вклад) |
Bormas (обсуждение | вклад) (→Задача) |
||
| Строка 1: | Строка 1: | ||
| − | = Задача = | + | = Свойства и структура алгоритмов = |
| + | |||
| + | == Задача == | ||
Пусть <math> X_1, X_2,...X_n </math> - независимые одинаково распределенные случайные величины с общей функцией распределения | Пусть <math> X_1, X_2,...X_n </math> - независимые одинаково распределенные случайные величины с общей функцией распределения | ||
Версия 16:08, 9 октября 2017
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Задача
- 1.2 Свойства и структура алгоритмов
- 1.3 Математическое описание алгоритма
- 1.4 Вычислительное ядро алгоритма
- 1.5 Макроструктура алгоритма
- 1.6 Схема реализации последовательного алгоритма
- 1.7 Последовательная сложность алгоритма
- 1.8 Информационный граф
- 1.9 Ресурс параллелизма алгоритма
- 1.10 Входные и выходные данные алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Задача
Пусть [math] X_1, X_2,...X_n [/math] - независимые одинаково распределенные случайные величины с общей функцией распределения [math] F(x) [/math], для которой при [math] x \to +\infty [/math] имеет место следующее представление:[math] F(x)=1-C(lnx)^{\beta-1}x^{-\alpha} [/math], где [math] C \gt 0 , \alpha \gt 0, \forall \beta [/math].
Методом статистического анализа показать, что [math] \lim_{n \to \infty}F(X_n^{(n)}) = \exp{x^{-\alpha}}, x \gt 0 [/math] и найти коэффициенты [math] a_n \gt 0 [/math].
Построить гистограмму статистики [math] T_n = \frac{X_n^{(n)}}{a_n} [/math] для функции [math] F(x) = 1 - \frac{2\sqrt{\ln{2}}}{(x+1)\sqrt{\ln{(x+1)}}}, x \gt 1 [/math] и сравнить её с функцией предельного распределения.
1.2 Свойства и структура алгоритмов
1) Сначала генерируем [math]n[/math] случайных величин [math] X_1, X_2,..., X_n [/math] из непрерывной функции распределения
2) Далее берем [math] X_n^{(n)} = X_n [/math], то есть максимально возможный элемент выборки из [math]n[/math] элементов
3) Затем делим [math] X_n^{(n)} [/math] на [math] a_k [/math], получая наш первый элемент статистики [math] \frac{X_n^{(n)}}{a_1} [/math]
4) Далее повторяем пункты 1) - 3) и генерируем столько статистик, сколько нам нужно. Чем больше статистик мы сгенерируем, тем более точная будет гистограмма
1.3 Математическое описание алгоритма
Обозначим за [math] \overline{F}(x) = 1 - F(x) [/math]
Рассмотрим [math] \frac{\overline{F}(tx)}{\overline{F}(x)} = \frac{C(\ln{tx})^{\beta-1}(tx)^{-\alpha} }{C(\ln{x})^{\beta-1}x^{-\alpha}} \to t^{-\alpha} [/math] при [math]x \to \infty [/math] [math] \Rightarrow [/math] [math] F(x) \in MDA(\Phi_\alpha)[/math], то есть принадлежит классу предельных распределений Фреше
Теперь найдем [math] a_n [/math]:
[math] \overline{F}(x) \sim C(\ln{x})^{\beta-1}x^{-\alpha}[/math] при [math]x \to \infty [/math], [math] \overline{F}(a_n) \sim \frac{1}{n}[/math] [math] \Rightarrow [/math]
[math] \ln{[C(lna_n)^{\beta-1}a_n^{-\alpha}]} = \ln{\frac{1}{n}}[/math]
[math] \ln{C} + (\beta-1)\ln{\ln{a_n}} - \alpha \ln{a_n} = -\ln{n}[/math]
[math] \alpha \ln{a_n} - (\beta-1)\ln{\ln{a_n}} - \ln{C} = \ln{n}[/math]
Будем искать [math] \ln{a_n} [/math] в виде: [math] \ln{a_n} = \frac{1}{\alpha}(\ln{n} + \ln{r_n})[/math], где [math] \ln{r_n} = \overline{O}(\ln{n})[/math]
[math] \ln{C} + (\beta-1)\ln{[\frac{1}{\alpha}(\ln{n} + \ln{r_n})]} - \ln{n} - \ln{r_n} = -\ln{n} [/math]
[math] \ln{r_n} \simeq \ln{C} - (\beta - 1)\ln{\alpha} + (\beta - 1)\ln{\ln{n}} = \ln{(C(\ln{n})^{\beta - 1}\alpha^{-(\beta - 1)})} [/math] - подставляем это в [math] \ln{a_n} [/math]
[math] \ln{a_n} \sim \frac{1}{\alpha}(\ln{n} + \ln{(C(\ln{n})^{\beta - 1}\alpha^{-(\beta - 1)})}) [/math]
[math] a_n = (\frac{Cn(\ln{n})^{\beta-1}}{\alpha^{\beta - 1}})^{\frac{1}{\alpha}}[/math]
В частном случае (из функции распределения):
[math] C = 2\sqrt{\ln{2}}; \alpha = 1; \beta = \frac{1}{2} [/math] - находятся путём подставления в [math] \overline{F}(a_nx) = \frac{2\sqrt{\ln{2}}}{(x + 1)\sqrt{\ln{(x + 1)}}} [/math]
[math] a_n = \frac{2\sqrt{\ln{2}}n}{\sqrt{\ln{n}}} [/math]
Из свойства класса распределений Фреше:
[math] P(X_n^{(n)} \lt xa_n) \to \begin{cases} e^{-\frac{1}{x}} &, x \gt 0 \\ 0 &, x \le 0 \end{cases} [/math]
[math] \Downarrow [/math]
[math] P(\frac{X_n^{(n)}}{a_n} \lt x) \to \begin{cases} e^{-\frac{1}{x}} &, x \gt 0 \\ 0 &, x \le 0 \end{cases} [/math] - предельная функция распределения статистики
А сама статистика [math] \frac{X_n^{(n)}}{a_k} [/math] находится следующим образом:
1) Сначала генерируем какое-то количество случайных величин [math] X_1, X_2,..., X_n [/math]
2) Далее берем [math] X_n^{(n)} = X_n [/math], то есть максимально возможный элемент выборки
3) Затем делим [math] X_n^{(n)} [/math] на [math] a_k [/math], получая наш первый элемент статистики [math] \frac{X_n^{(n)}}{a_1} [/math]
4) Далее повторяем пункты 1) - 3) и чем больше статистик мы сгенерируем, тем более точная будет гистограмма
Затем нам нужно сравнить гистограмму статистики с функцией предельного распределения.
1.4 Вычислительное ядро алгоритма
Для того, чтобы задача работала быстрее, имеет смысл создание каждого элемента статистики вынести на отдельные ядра. Самым трудоемким процессом является процесс создания случайной величины из наперед заданной функции распределения.
Алгоритм образования случайных чисел с непрерывным законом распределения ("Аппроксимация распределений" Пагуровой В.И):
Пусть [math] U [/math] означает случайную величину с равномерным законом распределения [math] U(0, 1), F(x) [/math] -абсолютно непрерывная ф.р., тогда величина [math] X = F^{-1}(U) [/math] имеет ф.р. [math] F(x) [/math]. Предполагается, что случайная величина изменяется в конечной области [math] (a,b). [/math] Если область бесконечна, то в вычислительных целях следует обрезать её, например, в точках [math] a [/math] и [math] b. [/math] Тогда случайная величина будет изменяться в этой конечной области.
Пусть требуется генерировать значения случайной величины [math] X [/math] с плотностью распределения [math] f(x), f(x) \gt 0 [/math] для [math] x \subseteq [a,b], f(x) = 0 [/math] для [math] x \nsubseteq [a,b].[/math] Обозначим [math] f = \max_{x \subseteq [a,b]}f(x). [/math] Образуем пару [math] (U_1, U_2), U_1 \sim U(0,1), U_2 \sim U(0,1). [/math] Вычисляем [math] X = a + (b - a)U_2. [/math] Если [math] U_1 \lt f(X)/f [/math], то принимаем [math] X [/math] в качестве требуемой случайной величины, в противном случае пару [math] (U_1, U_2) [/math] отбрасываем и все начинаем сначала. Метод основан на том факте, что если [math] U_1 \sim U(0,1), U_2 \sim U(0,1), U_1 [/math] и [math] U_2 [/math] независимы, тогда условная плотность распределения величины [math] a + (b - a)U_2 [/math] при условии [math] U_1 \lt f(a + (b - a)U_2)/f [/math] равна [math] f(x) [/math].
В нашей задача функция [math] f(x) = \frac{\sqrt{\ln{2}}(2\ln{(x + 1)} + 1)}{(x + 1)^2(\ln{(x + 1)})^{\frac{3}{2}}}, x \gt 1 [/math]
Сдвинем [math] x [/math] для удобства, таким образом: [math] f(x) = \frac{\sqrt{\ln{2}}(2\ln{(x + 2)} + 1)}{(x + 2)^2(\ln{(x + 2)})^{\frac{3}{2}}}, x \gt 0 [/math]
Эта функция невозрастающая, поэтому [math] f_{max} [/math] достигается при [math] x = 0 [/math], таким образом: [math] f_{max} = \frac{\sqrt{\ln{2}}(2\ln{(2)} + 1)}{(2)^2(\ln{(2)})^{\frac{3}{2}}} [/math]
Теперь у нас есть все необходимые данные для построения статистики [math] \frac{X_n^{(n)}}{a_k}. [/math]
1.5 Макроструктура алгоритма
Данную задачу я разделил на 2 программы. Первая программа занимается созданием статистики, а вторая программа строит совместный график данной статистики и предельной функции распределения используя удобную библиотеку matplotlib на языке python. Выбор matplotlib обусловлен тем, что на выходе мы получаем красивый и наглядный PDF-файл с гистограммой. Первая программа реализована на языке C с использованием технологии MPI, которая дает возможность вынести вычисление каждой статистики на отдельное ядро, причем одно ядро занимается сбором информации и созданием файла со статистиками, который в свою очередь пойдет на вход второй программы на python'e. Изначально при размере статистики равной 500 и каждой выборки равной 200 однопроцессная программа на python'e работала в районе 30 мин. А для большей точности графика (чтобы исключить стохастичность), нужен больший объем выборки. В следствие этого, появилась потребность в распараллеливании.
1.6 Схема реализации последовательного алгоритма
1) Генерируем 2 случайные величины [math] U_1, U_2 [/math] с равномерным законом распределения от 0 до 1
2) Задаем некоторый [math] x = a - (b - a)*U_2 [/math]
3) Находим [math] f(x) [/math]
4) Проверяем [math] U_1 \lt \frac{f(x)}{f_{max}} [/math], где [math] f_{max}[/math] - некоторая заранее известная константа
5) Если условие выполняется, то запоминаем [math] x [/math] в массив, иначе повторяем пункты 1)-4) заново до тех пор, пока условие не выполнится
6) Выбираем максимальный элемент выборки
7) Делим этот элемент на [math] a_k [/math], таким образом получая статистику [math] \frac{X_n^{(n)}}{a_k}[/math]
8) Проверяем эту статистику на "масштаб", то есть для отрисовки гистограммы берем статистики удовлетворяющие условию [math] \frac{X_n^{(n)}}{a_k} \lt scale[/math]. Где [math] scale [/math] - верхняя граница оси абсцисс(для защиты от случайных выбросов). При выполнении этого условия, записываем эту статистику в массив статистик, иначе начинаем пункты 1)-7) заново
9) Заполняем массив статистик, то есть выполняем пункты 1)-8) столько раз, сколько нам нужно
1.7 Последовательная сложность алгоритма
Сложность алгоритма оценить невозможно, так как есть элемент случайности, из-за которого нельзя понять, сколько операций мы сможем совершить, прежде чем мы сгенерируем случайную величину.
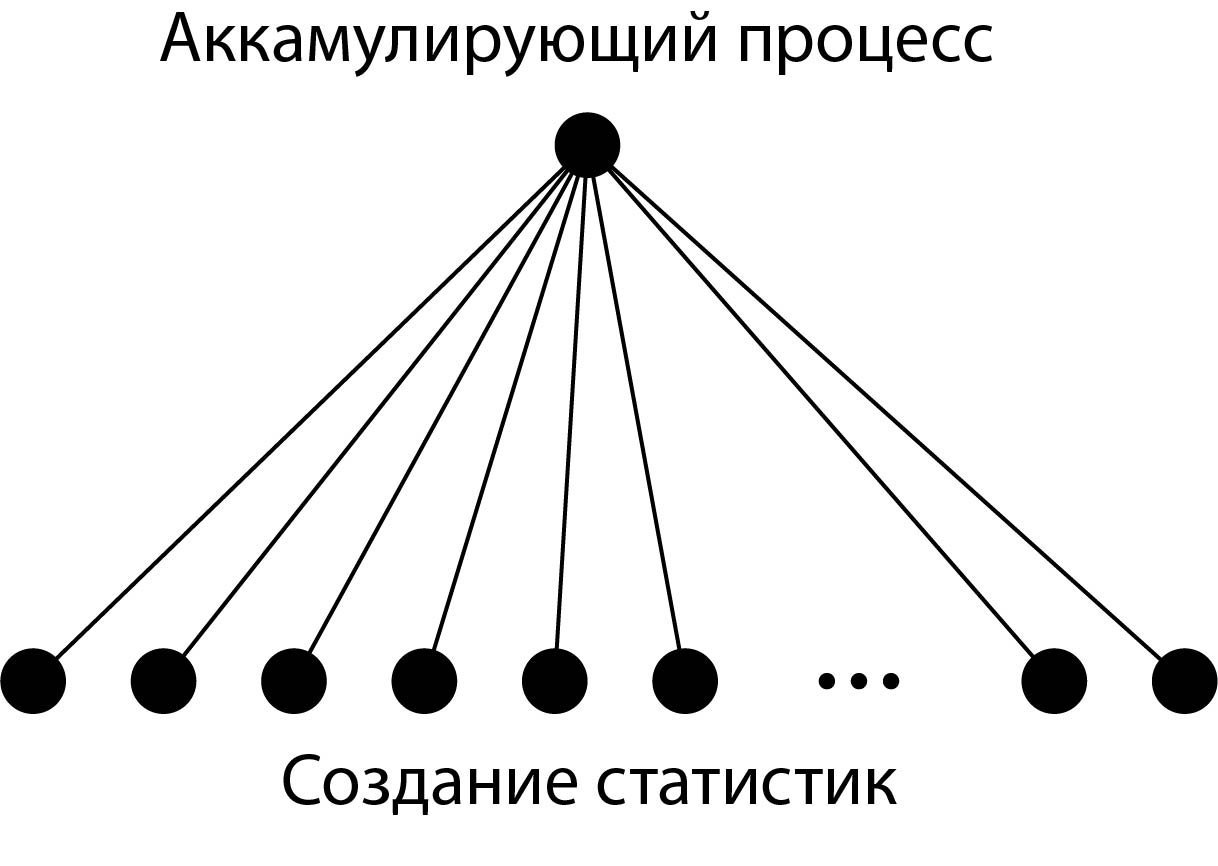
1.8 Информационный граф
1.9 Ресурс параллелизма алгоритма
Данный алгоритм для статистики размера [math] N [/math] работает в [math] N [/math] раз быстрее чем последовательный, так как вычисление каждой статистики моно вынести в отдельный процесс, но при слишком большой выборке "узким горлышком" системы может оказаться первый процесс, который принимает все сообщения от других процессов, но эта задержка так незначительна, что ей можно пренебречь.
1.10 Входные и выходные данные алгоритма
Для нашей программы нужно ввести 2 параметра. N - количество случайных величин для каждой статистики T - количество статистик. По сути это число равно количеству процессов + 1, которые нужно запустить на машине чтобы получить T статистик
2 Программная реализация алгоритма
2.1 Масштабируемость алгоритма и его реализации
Так как фиксированной вычислительной сложности установить невозможно, то обозначим усредненную за [math] W [/math]. И сильная и слабая масштабируемости почти линейно зависят от количества параллельно запущенных процессов, ведь каждый процесс независимо от других производит одноразовую генерацию случайных величин, которые затем поступают на аккамулирующий процесс(см. схему) для образования файла со статистиками. Как уже говорилось, издержки могут быть вызваны большим количеством информации передаваемое аккамулирующему процессу, но эти издержки столь незначительны, что ими можно пренебречь. Тем более в данной задачи имеет смысл рассматривать не более 2000 статистик, поэтому такое количество процессов смогут быстро передать результаты "слушающему" процессу.
2.2 Существующие реализации алгоритма
На своей практике мною подобные алгоритмы встречены не были
3 Литература
Курс лекций от Sharcnet HPC [[1]]
Аппроксимация распределений Пагурова В.И.