Блочная прогонка: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Frolov (обсуждение | вклад) (Заготовка из точечной) |
Frolov (обсуждение | вклад) |
||
| Строка 14: | Строка 14: | ||
=== Общее описание алгоритма === | === Общее описание алгоритма === | ||
| − | ''' | + | '''Блочная прогонка''' - один из вариантов метода исключения неизвестных в приложении к решению СЛАУ<ref name="VOLA">Воеводин В.В. Вычислительные основы линейной алгебры. М.: Наука, 1977.</ref><ref name="MIV">Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: Наука, 1984.</ref> вида <math>Ax = b</math>, где |
:<math> | :<math> | ||
A = \begin{bmatrix} | A = \begin{bmatrix} | ||
| − | + | A_{11} & A_{12} & 0 & \cdots & \cdots & 0 \\ | |
| − | + | A_{21} & A_{22} & A_{23}& \cdots & \cdots & 0 \\ | |
| − | 0 & | + | 0 & A_{32} & A_{33} & \cdots & \cdots & 0 \\ |
\vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ | \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ | ||
| − | 0 & \cdots & \cdots & | + | 0 & \cdots & \cdots & A_{n-1 n-2} & A_{n-1 n-1} & A_{n-1 n} \\ |
| − | 0 & \cdots & \cdots & 0 & | + | 0 & \cdots & \cdots & 0 & A_{n n-1} & A_{n n} \\ |
\end{bmatrix}, x = \begin{bmatrix} | \end{bmatrix}, x = \begin{bmatrix} | ||
| − | + | X_{1} \\ | |
| − | + | X_{2} \\ | |
\vdots \\ | \vdots \\ | ||
| − | + | X_{n} \\ | |
\end{bmatrix}, b = \begin{bmatrix} | \end{bmatrix}, b = \begin{bmatrix} | ||
| − | + | B_{1} \\ | |
| − | + | B_{2} \\ | |
\vdots \\ | \vdots \\ | ||
| − | + | B_{n} \\ | |
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
| − | Часто, однако, при изложении сути метода прогонки<ref name="SETKI">Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. М.: Наука, 1978.</ref> элементы правой части и матрицы системы обозначают и нумеруют по-другому, например СЛАУ может иметь вид (<math>N=n+1</math>) | + | Часто, однако, при изложении сути метода блочной прогонки<ref name="SETKI">Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. М.: Наука, 1978.</ref> элементы правой части и матрицы системы обозначают и нумеруют по-другому, например СЛАУ может иметь вид (<math>N=n+1</math>) |
:<math> | :<math> | ||
A = \begin{bmatrix} | A = \begin{bmatrix} | ||
| − | + | C_{0} & -B_{0} & 0 & \cdots & \cdots & 0 \\ | |
| − | - | + | -A_{1} & C_{1} & -B_{1} & \cdots & \cdots & 0 \\ |
| − | 0 & - | + | 0 & -A_{2} & C_{2} & \cdots & \cdots & 0 \\ |
\vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ | \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ | ||
| − | 0 & \cdots & \cdots & - | + | 0 & \cdots & \cdots & -A_{N-1} & C_{N-1} & -B_{N-1} \\ |
| − | 0 & \cdots & \cdots & 0 & - | + | 0 & \cdots & \cdots & 0 & -A_{N} & C_{N} \\ |
\end{bmatrix}\begin{bmatrix} | \end{bmatrix}\begin{bmatrix} | ||
| − | + | Y_{0} \\ | |
| − | + | Y_{1} \\ | |
\vdots \\ | \vdots \\ | ||
| − | + | Y_{N} \\ | |
\end{bmatrix} = \begin{bmatrix} | \end{bmatrix} = \begin{bmatrix} | ||
| − | + | F_{0} \\ | |
| − | + | F_{1} \\ | |
\vdots \\ | \vdots \\ | ||
| − | + | F_{N} \\ | |
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
| − | или, если записывать отдельно по уравнениям, то | + | или, если записывать отдельно по блочным уравнениям, то |
:<math> | :<math> | ||
| − | + | С_{0} Y_{0} - B_{0} Y_{1} = F_{0},\\ | |
| − | - | + | -A_{i} Y_{i-1} + C_{i} Y_{i} - B_{i} Y_{i+1} = F_{i}, 1 \le i \le N-1, \\ |
| − | - | + | -A_{N} Y_{N-1} + C_{N} Y_{N} = F_{N} |
</math> | </math> | ||
Версия 13:34, 10 августа 2015
| Прогонка для трёхдиагональной матрицы, точечный вариант | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]8n-7[/math] |
| Объём входных данных | [math]4n-2[/math] |
| Объём выходных данных | [math]n[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]3n-2[/math] |
| Ширина ярусно-параллельной формы | [math]2[/math] |
Основные авторы описания: А.В.Фролов
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Описание ресурса параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Блочная прогонка - один из вариантов метода исключения неизвестных в приложении к решению СЛАУ[1][2] вида [math]Ax = b[/math], где
- [math] A = \begin{bmatrix} A_{11} & A_{12} & 0 & \cdots & \cdots & 0 \\ A_{21} & A_{22} & A_{23}& \cdots & \cdots & 0 \\ 0 & A_{32} & A_{33} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & A_{n-1 n-2} & A_{n-1 n-1} & A_{n-1 n} \\ 0 & \cdots & \cdots & 0 & A_{n n-1} & A_{n n} \\ \end{bmatrix}, x = \begin{bmatrix} X_{1} \\ X_{2} \\ \vdots \\ X_{n} \\ \end{bmatrix}, b = \begin{bmatrix} B_{1} \\ B_{2} \\ \vdots \\ B_{n} \\ \end{bmatrix} [/math]
Часто, однако, при изложении сути метода блочной прогонки[3] элементы правой части и матрицы системы обозначают и нумеруют по-другому, например СЛАУ может иметь вид ([math]N=n+1[/math])
- [math] A = \begin{bmatrix} C_{0} & -B_{0} & 0 & \cdots & \cdots & 0 \\ -A_{1} & C_{1} & -B_{1} & \cdots & \cdots & 0 \\ 0 & -A_{2} & C_{2} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & -A_{N-1} & C_{N-1} & -B_{N-1} \\ 0 & \cdots & \cdots & 0 & -A_{N} & C_{N} \\ \end{bmatrix}\begin{bmatrix} Y_{0} \\ Y_{1} \\ \vdots \\ Y_{N} \\ \end{bmatrix} = \begin{bmatrix} F_{0} \\ F_{1} \\ \vdots \\ F_{N} \\ \end{bmatrix} [/math]
или, если записывать отдельно по блочным уравнениям, то
- [math] С_{0} Y_{0} - B_{0} Y_{1} = F_{0},\\ -A_{i} Y_{i-1} + C_{i} Y_{i} - B_{i} Y_{i+1} = F_{i}, 1 \le i \le N-1, \\ -A_{N} Y_{N-1} + C_{N} Y_{N} = F_{N} [/math]
Суть метода - в исключении из уравнений неизвестных, сначала - сверху вниз - под диагональю, а потом - снизу вверх - над диагональю.
1.2 Математическое описание алгоритма
В приведённых обозначениях в прогонке сначала выполняют её прямой ход - вычисляют коэффициенты
- [math] \alpha_{1} = b_{0}/c_{0},\\ \beta_{1} = f_{0}/c_{0}, \\ \alpha_{i+1} = b_{i}/(c_{i}-a_{i}\alpha_{i}), \quad i = 1, 2, \cdots , N-1, \\ \beta_{i+1} = (f_{i}+a_{i}\beta_{i})/(c_{i}-a_{i}\alpha_{i}), \quad i = 1, 2, \cdots , N. [/math]
после чего вычисляют решение с помощью обратного хода
- [math] y_{N} = \beta_{N+1}, \\ y_{i} = \alpha_{i+1} y_{i+1} + \beta_{i+1}, \quad i = N-1, N-2, \cdots , 1, 0. [/math]
В литературе[3] указывается, что данные формулы эквиваленты вычислению одного из [math]LU[/math]-разложений матрицы системы с последующим решением двухдиагональных систем методом обратной подстановки.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма можно представить из двух частей - прямого и обратного хода. В прямом ходе ядро составляют последовательности операций деления, умножения и сложения/вычитания. В обратном ходе в ядре остаются только последовательности умножения и сложения.
1.4 Макроструктура алгоритма
Кроме представления макроструктуры алгоритма как совокупности прямого и обратного хода, прямой ход также может быть разложен на две макроединицы - разложения матрицы и прямого хода решения двухдиагональной СЛАУ, которые выполняются "одновременно", т.е., параллельно друг другу. При этом решение двухдиагональной СЛАУ использует результаты разложения.
1.5 Схема реализации последовательного алгоритма
Последовательность исполнения метода следующая:
1. Инициализируется прямой ход прогонки:
- [math] \alpha_{1} = b_{0}/c_{0},\\ \beta_{1} = f_{0}/c_{0}, \\ [/math]
2. Последовательно для всех i от 1 до N-1 выполняются формулы прямого хода:
- [math] \alpha_{i+1} = b_{i}/(c_{i}-a_{i}\alpha_{i}), \\ \beta_{i+1} = (f_{i}+a_{i}\beta_{i})/(c_{i}-a_{i}\alpha_{i}). [/math]
3. Инициализируется обратный ход прогонки:
- [math] y_{N} = (f_{N}+a_{N}\beta_{N})/(c_{N}-a_{N}\alpha_{N}) [/math]
4. Последовательно для всех i с убыванием от N-1 до 0 выполняются формулы обратного хода:
- [math] y_{i} = \alpha_{i+1} y_{i+1} + \beta_{i+1}. [/math]
1.6 Последовательная сложность алгоритма
Для выполнения прогонки в трёхдиагональной СЛАУ из n уравнений с n неизвестными в последовательном (наиболее быстром) варианте требуется:
- [math]2n-1[/math] делений,
- [math]3n-3[/math] сложений/вычитаний,
- [math]3n-3[/math] умножений.
При классификации по последовательной сложности, таким образом, прогонка относится к алгоритмам с линейной сложностью.
1.7 Информационный граф
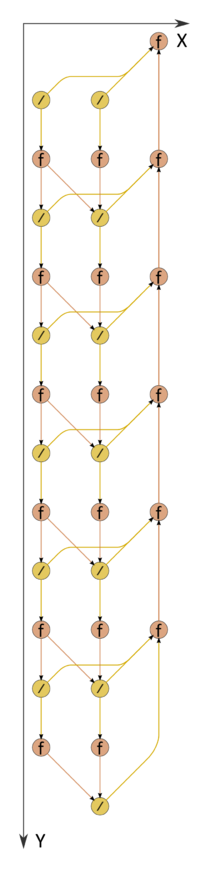
Информационный граф прогонки изображён на рис.1. Как видно, он почти последователен: при выполнении прямого хода две ветви (левая - разложение матрицы, центральная - решение первой из двухдиагональных систем) могут выполняться параллельно друг другу. Правая ветвь соответствует обратному ходу. По рисунку видно, что не только математическая суть обработки элементов векторов, но даже структура графа алгоритма и направление потоков данных в нём вполне соответствуют названию "обратный ход".
1.8 Описание ресурса параллелизма алгоритма
Для выполнения прогонки в трёхдиагональной СЛАУ из n уравнений с n неизвестными в параллельном варианте требуется последовательно выполнить следующие ярусы:
- [math]n[/math] ярусов делений (в каждом из ярусов, кроме одного, по 2 деления),
- по [math]2n - 2[/math] ярусов умножений и сложений/вычитаний (в n-1 ярусах - по 2 операции, в n-1 - по одной).
При классификации по высоте ЯПФ, таким образом, прогонка относится к алгоритмам со сложностью [math]O(n)[/math]. При классификации по ширине ЯПФ его сложность будет [math]2[/math].
1.9 Входные и выходные данные алгоритма
Входные данные: трёхдиагональная матрица [math]A[/math] (элементы [math]a_{ij}[/math]), вектор [math]b[/math] (элементы [math]b_{i}[/math]).
Выходные данные: вектор [math]x[/math] (элементы [math]x_{i}[/math]).
Объём выходных данных: [math]n[/math].
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности, как хорошо видно, является константой (причём менее 2).
При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – тоже константа.
Алгоритм полностью детерминирован.
Обычно прогонка используется для решения СЛАУ с диагональным преобладанием. Тогда гарантируется устойчивость алгоритма. В случае, когда требуется решение нескольких СЛАУ с одной и той же матрицей, левую ветвь вычислений (см. рисунок с графом алгоритма) можно не повторять. Это связано с тем, что [math]LU[/math]-разложение матрицы системы не нужно перевычислять.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
В зависимости от нужд вычислений, возможны как разные способы хранения матрицы СЛАУ (в виде одного массива с 3 строками или в виде 3 разных массивов), так и разные способы хранения вычисляемых коэффициентов (на месте использованных уже элементов матрицы либо отдельно).