Участник:Diana Pimenova/Алгоритм Фокса умножения матриц: различия между версиями
| Строка 163: | Строка 163: | ||
== Существующие реализации алгоритма == | == Существующие реализации алгоритма == | ||
| + | Ссылки на существующие реализации этого алгоритма: | ||
| + | [http://www.hpcc.unn.ru/?dir=889] - центр суперкомпьютерных технологий Нижегородского Государственного Университета. | ||
| + | [http://www.intuit.ru/studies/courses/1156/190/lecture/4954?page=4] - ИНТУИТ | ||
= Литература = | = Литература = | ||
<references /> | <references /> | ||
Версия 21:17, 15 ноября 2017
Автор: Д.В.Пименова
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Метод Фокса - это блочный алгоритм умножения квадратных матриц. Основная его идея заключается в том, что матрицы разбиваются на части, представляющие собой подматрицы исходных матриц (разделяются как матрицы-операнды, так и результирующая). При таком разбиении данных для определения базовых подзадач за основу берутся вычисления, выполняемые над блоками. А базовой подзадачей является процедура вычисления всех элементов одного из блоков результирующей матрицы. В отличие от стандартного ленточного алгоритма, когда мы рассматриваем матрицы в виде набора строк и столбцов, такой подход хранения позволяет добиться большей локализации данных и повысить эффективность использования кэш-памяти, что дает нам уменьшение времени работы программы.[1]
1.2 Математическое описание алгоритма
Исходные данные: квадратная матрица [math]A[/math] (состоит из блоков [math]A_{ij}[/math]), квадратная матрица [math]B[/math] (состоит из блоков [math]B_{ij}[/math]).
Вычисляемые данные: квадратная матрица [math]C[/math] (состоит из блоков [math]C_{ij}[/math]).
При этом каждый блок [math]C_{ij}[/math] определяется как произведение соответствующих блоков матриц [math]A[/math] и [math]B[/math] :
- [math] \begin{align} C_{ij} = \sum_{s = 0}^{q-1} A_{is} B_{sj}, \quad i \in [0, q-1],\quad j \in [0, q-1]. \end{align} [/math]
1.3 Вычислительное ядро алгоритма
Вычислительное ядро перемножения квадратных матриц методом Фокса можно составить из процедур вычисления всех элементов одного из блоков результирующей матрицы, т.е. из процедур множественных вычислений умножения блоков матрицы [math]A[/math] на блоки матрицы [math]B[/math]
- [math] \begin{align} \sum_{s = 0}^{q-1} A_{is} B_{sj}, \quad i \in [0, q-1],\quad j \in [0, q-1]. \end{align} [/math]
1.4 Макроструктура алгоритма
Как уже записано в описании ядра алгоритма, основную часть умножения матриц составляют множественные вычисления произведения блоков матрицы [math]A[/math] на блоки матрицы [math]B[/math]. Перемножать блоки будем стандартным методом, используя определение произведения матриц:
- [math] \begin{align} \sum_{k = 1}^{n} a_{ik} b_{kj} \end{align} [/math]
1.5 Схема реализации последовательного алгоритма
Разобьем исходные матрицы на блоки [math]A_{ij}[/math],[math]B_{ij}[/math] и [math]C_{ij}[/math] соответственно. Обнулим блоки матрицы [math]C[/math], предназначенной для хранения соответствующего результирующего произведения [math]AB[/math]. Затем запускается цикл, в ходе которого выполняется последовательное умножение блоков матриц операндов и суммирование полученных результатов.
- [math] \begin{align} С_{ij} = \sum_{s = 0}^{q-1} A_{is} B_{sj}, \quad i \in [0, q-1],\quad j \in [0, q-1]. \end{align} [/math]
После завершения цикла мы получим матрицу с блоками [math]C_{ij}[/math], соответствующую произведению [math]AB[/math].[3]
1.6 Последовательная сложность алгоритма
Рассмотрим квадратные матрицы размером [math]n \times n[/math] , разбитые на блоки размера [math]\frac{n}{q}[/math] . Итого у нас получается [math]q \times q[/math] блоков.
Для умножение данных матриц в последовательном варианте требуется по [math] n^3 [/math] умножений и сложений.
При классификации по последовательной сложности, таким образом, алгоритм умножения матриц относится к алгоритмам с кубической сложностью.
1.7 Информационный граф
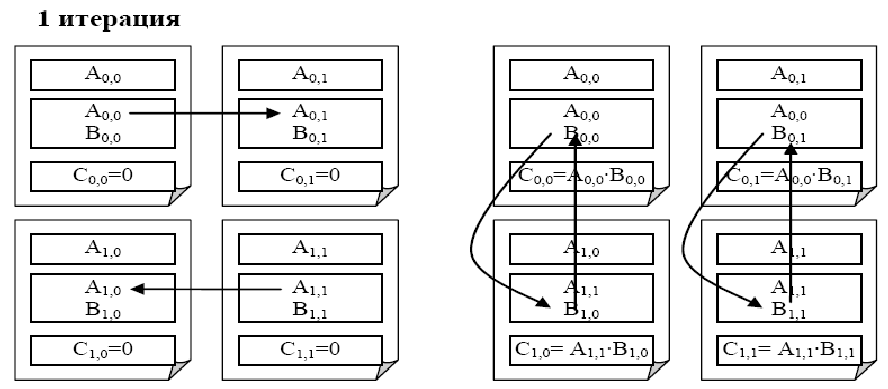
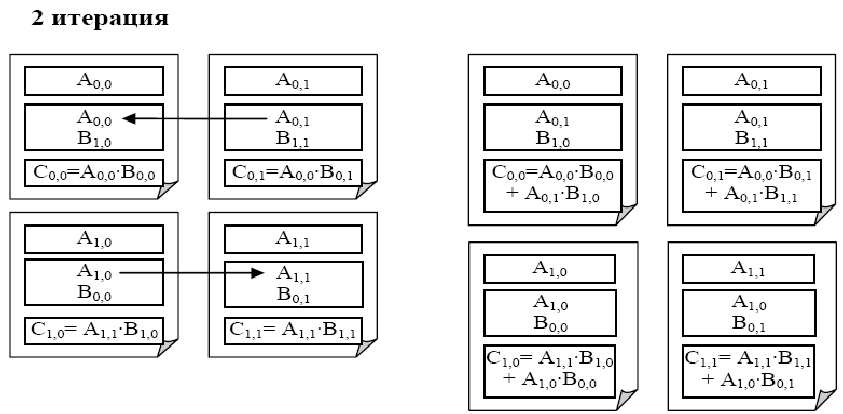
Сначала опишем идею параллельного умножения матриц методом Фокса:
- Каждой подзадаче [math](i,j)[/math] передаются блоки [math]A_{ij}[/math], [math]B_{ij}[/math] и обнуляются блоки [math]C_{ij}[/math] на всех подзадачах.
- Для каждой строки [math]i[/math] блок [math]A_{ij}[/math] подзадачи [math](i,j)[/math] пересылается на все подзадачи той же строки [math]i[/math] решетки.
- Полученные в результаты пересылок блоки [math]A'_{ij}[/math], [math]B'_{ij}[/math] каждой подзадачи [math](i,j)[/math] перемножаются и прибавляются к блоку [math]C_{ij}[/math][math]: C_{ij} = C_{ij} + A'_{ij}B'_{ij} [/math].
- блоки [math]B'_{ij}[/math] каждой подзадачи [math](i,j)[/math] пересылаются подзадачам, являющимися соседями сверху в столбцах решетки подзадач (блоки подзадач из первой строки решетки пересылаются подзадачам последней строки решетки).
1.8 Ресурс параллелизма алгоритма
Определим вычислительную сложность данного алгоритма. Пусть все матрицы являются квадратными размера [math]n \times n[/math] , количество блоков по горизонтали и вертикали являются одинаковым и равным [math] q [/math] (т.е. размер всех блоков равен [math]k \times k[/math] , где [math]k = \frac{n}{q}[/math] ), процессоры образуют квадратную решетку и их количество равно [math]p = q^{2}[/math] .
Алгоритм Фокса требует для своего выполнения [math]q[/math] итераций, в ходе которых каждый процессор перемножает свои текущие блоки матриц [math]A[/math] и [math]B[/math] и прибавляет результаты умножения к текущему значению блока матрицы [math]C[/math] . С учетом выдвинутых предположений общее количество выполняемых при этом операций будет иметь порядок [math]\frac{n^{3}}{p}[/math] .
Определим количество вычислительных операций. Сложность выполнения скалярного умножения строки блока матрицы [math]A[/math] на столбец блока матрицы [math]B[/math] можно оценить как[math]2\frac{n}{q} - 1[/math] . Количество строк и столбцов в блоках равно [math]\frac{n}{q}[/math] и, как результат, трудоемкость операции блочного умножения оказывается равной [math]\frac{\frac{n^2}{p}}{\frac{2n}{q} - 1}[/math]. Для сложения блоков требуется[math]\frac{n^{2}}{p}[/math] операций.
1.9 Входные и выходные данные алгоритма
Входные данные: матрица [math]A[/math] (элементы [math]a_{ij}[/math]), матрица [math]B[/math] (элементы [math]b_{ij}[/math])).
Объём входных данных: [math]2n^{2}[/math]
Выходные данные: матрица [math]C[/math] (элементы [math]c_{ij}[/math]).
Объём выходных данных: [math]n^{2}[/math]
2 Программная реализация алгоритма
2.1 Масштабируемость алгоритма и его реализации
2.1.1 Масштабируемость алгоритма
Возьмем квадратные матрицы размерностью [math]n \times n[/math], где [math]500\leqslant n \leqslant 2000[/math], а число процессов будем изменять от [math]2[/math] до [math]128[/math]. В качестве примера приведем время выполнения программы в зависимости от числа процессов при фиксированном размере матриц [math]n = 2000[/math].
| Число процессов | Время (с) |
|---|---|
| 128 | 0.510 |
| 64 | 1.038 |
| 32 | 2.556 |
| 16 | 5.121 |
| 8 | 20.844 |
| 4 | 20.952 |
| 2 | 92.919 |
Далее рассмотрим зависимость времени выполнения программы от размера матриц. Число процессов также зафиксируем: возьмем [math]64[/math] процесса.
| Размер матриц | Время (с) |
|---|---|
| 2000 | 1.038 |
| 1500 | 0.409 |
| 1000 | 0.115 |
| 750 | 0.049 |
| 500 | 0.015 |
Из приведенных результатов исследования видно, что система хорошо масштабируема.
2.1.2 Характеристики программно-аппаратной среды
Все вычисления были произведены на суперкомпьютере "Ломоносов".
Для компиляции был использован компилятор языка C++ GNU 4.4.6.
Вычисления производились в очереди test. Ограничений на лимит времени на узел наложено не было.
2.2 Существующие реализации алгоритма
Ссылки на существующие реализации этого алгоритма: [1] - центр суперкомпьютерных технологий Нижегородского Государственного Университета. [2] - ИНТУИТ
3 Литература
- ↑ Лекции по высокопроизводительным вычислительным системам СПбГПУ, 2016.
- ↑ http://it.kgsu.ru/ParalAlg/palg046.html
- ↑ Абрамян М.Э. Лекции по основам параллельного программирования, ЮФУ, 2016.