Алгоритм Пурдома: различия между версиями

[выверенная версия]

[непроверенная версия]

Версия 03:06, 18 ноября 2017

Алгоритм Пурдома
Последовательный алгоритм
Последовательная сложность	[math]O(\|E\| + \mu^2)[/math]
Объём входных данных	[math]O(\|E\| + \|V\|)[/math]
Объём выходных данных	[math]O(\|V\|^2)[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]N/A [/math]
Ширина ярусно-параллельной формы	[math]N/A[/math]

Основные авторы описания: И.В.Афанасьев

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм Пурдома^[1] находит транзитивное замыкание ориентированного графа за время [math]O(|E| + \mu |V|)[/math], где [math]\mu \le |E|[/math] – число компонент сильной связности этого графа. Алгоритм может быть модифицирован для проверки принадлежности к транзитивному замыканию множества заданных пар вершин.

1.2 Математическое описание алгоритма

Алгоритм основан на следующих свойствах:

Если вершины [math]v[/math] и [math]w[/math] принадлежат одной компоненте сильной связности графа [math]G[/math], то его транзитивное замыкание [math]G^+[/math] содержит рёбра [math](v, w)[/math] и [math](w, v)[/math].
Если вершины [math]x[/math] и [math]y[/math] принадлежат одной компоненте сильной связности графа [math]G[/math], а вершины [math]z[/math] и [math]t[/math] – другой, то рёбра [math](x, z)[/math], [math](x, t)[/math], [math](y, z)[/math], [math](y, t)[/math] принадлежат или не принадлежат транзитивному замыканию [math]G^+[/math] одновременно.

Таким образом, поиск транзитивного замыкания графа [math]G[/math] сводится к поиску транзитивного замыкания ациклического графа [math]\tilde G[/math], полученного из [math]G[/math] схлопыванием каждой компоненты сильной связности в одну вершину. Транзитивное замыкание ациклического графа вычисляется с использованием топологической сортировки вершин графа.

1.3 Вычислительное ядро алгоритма

Алгоритм состоит из трех важных вычислительных частей, для каждой из которых важно оценить относительное время выполнения относительно других частей.

Поиск сильно связанных компонент в исходном графе
Построение графа промежуточного представления
Поиски в ширину в графе промежуточного представления для построения итогового транзитивного замыкания

1. В случае решения задачи проверки принадлежности к транзитивному замыканию множества заданных пар вершин, соотношение объемов различных вычислительных частей алгоритма может быть очень различным и, очевидно, зависит от числа пар входных вершин. Кроме того, данное соотношение может также зависеть от типа входного графа, так как структура и количество сильно-связанных компонент сильно влияют как на время поиска сильно-связанных компонент, так и на время выполнения поисков в ширину. Далее представлена таблица, демонстрирующая процент времени выполнения данных частей для одной из реализаций алгоритма для различных типов графов с числом вершин [math]2^{23}[/math], и числом входных пар вершин для проверки равным 10000.

Рисунок 1. Сравнение времени выполнения различных частей одной из реализаций алгоритма Пурдома.

Важно заметить, что некоторые алгоритмы поиска сильно-связанных компонент (например, DCSC) также основываются на поисках в ширину. Таким образом, вычислительным ядром алгоритма можно считать поиск в ширину. В свою очередь вычислительным ядром алгоритма поиска в ширину является обход вершин, смежных с выбранной вершиной, с последующим добавлением еще не посещенных вершин в множество "передовых" вершин.

2. В случае решения задачи поиска полного транзитивного замыкания наиболее вычислительно затратной частью являются поиски в ширину в графе промежуточного представления, так как его необходимо произвести от всех вершин данного графа, число которых может быть значительным при большом числе сильно-связанных компонент в исходном графе.

1.4 Макроструктура алгоритма

Вычисления производятся в четыре этапа:

Найти компоненты сильной связности исходного графа, заменить каждую компоненту на одну вершину и удалить образовавшиеся рёбра-петли.
Выполнить топологическую сортировку полученного ациклического графа [math]\tilde G[/math].
Вычислить транзитивное замыкание графа [math]\tilde G[/math], двигаясь от вершин с бо́льшими номерами к меньшим.
По найденному транзитивному замыканию [math]\tilde G[/math] восстановить транзитивное замыкание исходного графа.

Последний этап не является обязательным, если рассматривать транзитивное замыкание [math]\tilde G[/math] как «упакованное» транзитивное замыкание [math]G[/math].

1.5 Схема реализации последовательного алгоритма

1 этап (вычисление компонент сильной связности) может быть реализован алгоритмом Тарьяна^[2], находящим компоненты сильной связности в ходе поиска в глубину.

2 этап (топологическая сортировка) может быть реализован алгоритмом Кана^[3] либо последовательным применением поиска в глубину^[2] для нумерации вершин в предпорядке.

3 этап (транзитивное замыкание [math]\tilde G[/math]) выполняется следующим алгоритмом:

Входные данные:
    ациклический граф 'G с вершинами 'V, пронумерованными в топологическом порядке, и рёбрами E.
Выходные данные:
    для каждой вершины v ∈ V – набор вершин T(v),
        так что транзитивное замыкание G состоит из рёбер (v, w), v ∈ V, w ∈ T(v).
    
for each v ∈ V do T(v) := { v }
for v ∈ V in reverse order:
    for each (v, w) ∈ E do T(v) := T(v) ∪ T(w)

4 этап (транзитивное замыкание [math]G[/math]) либо выполняется следующим алгоритмом:

Входные данные
    граф G с вершинами V;
    компоненты сильной связности SCC(v) графа G;
    граф [math]\tilde G[/math] с вершинами [math]\tilde V[/math];
    транзитивное замыкание [math]\tilde T[/math] графа [math]\tilde G[/math].
Выходные данные:
    для каждой вершины v ∈ V – набор вершин T(v),
        так что транзитивное замыкание G состоит из рёбер (v, w), v ∈ V, w ∈ T(v).
        
for each v ∈ V do T(v) := { v }
for each v ∈ [math]\tilde V[/math]:
    for each w ∈ [math]\tilde T(v)[/math]:
        T(v) := T(v) ∪ SCC(w)
    for each x ∈ SCC(v):
        T(x) := T(v)    /* присваивание по ссылке */

либо транзитивное замыкание может строиться по упакованным данным [math]\tilde T(v)[/math] одной из следующих функций:

Входные данные
    граф G с вершинами V;
    компоненты сильной связности SCC(v) графа G;
    отображение R(v) вершин графа G на вершины графа [math]\tilde G[/math];
    граф [math]\tilde G[/math] с вершинами [math]\tilde V[/math];
    транзитивное замыкание [math]\tilde T[/math] графа [math]\tilde G[/math].
    
function transitive_closure(v):
    T := { v }
    for each w ∈ [math]\tilde T(R(v))[/math]:
        T := T ∪ SCC(w)
    return T
    
function is_in_transitive_closure(v, w):
    return R(w) ∈ [math]\tilde T(R(v))[/math]

1.6 Последовательная сложность алгоритма

Первый и второй этап выполняются с помощью поиска в глубину со сложностью [math]O(|E|)[/math].

На третьем этапе основой операцией является объединение списков вершин. В случае хранения списков в отсортированном виде объединение выполняется за линейное время. Количество списков не превосходит [math]|V|[/math], а в каждом списке не более [math]\mu[/math] вершин, где [math]\mu[/math] – количество компонент сильной связности. Общая сложность тогда составляет [math]O(\mu^2)[/math]. Альтернативным форматов хранения списка вершин является битовая маска с такой же общей сложностью.

Сложность четвёртого этапа составляет [math]O(\mu |V|)[/math], так как для каждой из [math]\mu[/math] компонент сильной связности за линейное время вычисляется список вершин из не более чем [math]|V|[/math] вершин. Поскольку компоненты сильной связности не пересекаются, на данном этапе уже не требуется хранить списки в отсортированном виде.

Таким образом, общая сложность составляет [math]O(|E| + \mu^2)[/math], если не требуется явное построение транзитивного замыкания, или [math]O(|E| + \mu |V|)[/math] в противном случае.

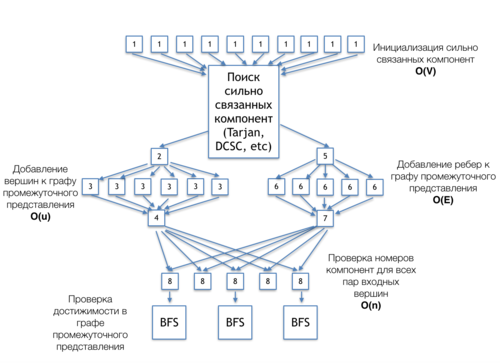
1.7 Информационный граф

На рисунке 2 представлен информационный граф алгоритма Пурдома, демонстрирующий связь между его основным частями. Алгоритм представлен для вариации постановки задачи, когда производится проверка принадлежности к транзитивному замыканию множества заранее заданных пар вершин.

Рисунок 2. Информационный граф алгоритма Пурдома.

[1] - инициализация массива номеров сильно связанных компонент

[Поиск сильно связанных компонент (Tarjan, DCSC, etc)] - независимый блок алгоритма, может быть реализован любым алгоритмом сильно связанных компонент: DCSC, Тарьяна и др. Информационный графы данных алгоритмов могут быть найдены в соответствующих разделах.

[2] - выделение памяти под вершины графа промежуточного представления

[3] - добавление вершин к графу промежуточного представления, каждая вершина соответствует одной сильно-связанной компоненте

[4] - подсчет числа вершин в графе промежуточного представления

[5] - выделение памяти под ребра графа промежуточного представления

[6] - добавление ребер к графу промежуточного представления, связывающих различные сильно связанные компоненты

[7] - подсчет числа ребер в графе промежуточного представления

[8] - проверка номеров сильно связанных компонент для каждой пары сильно связанных компонент

[BFS] - поиски в ширину от тех вершин, которые находятся в одних сильно связанных компонентах

1.8 Ресурс параллелизма алгоритма

В данном разделе будет описан ресурс параллелизма, основываясь на информационном графе алгоритма, приведенном на рисунке 2.

Инициализация сильно связанных компонент [1] может производиться параллельно и требует [math]|V|[/math] операций.

Поиск сильно связанных компонент может иметь различный ресурс параллелизма, в зависимости от выбора алгоритма.

Добавление вершин и ребер к графу промежуточного представления [2]-[7] требует [math]|E|[/math] и [math]|u|[/math] операций ([math]u[/math] - число сильно связанных компонент исходного графа), которые так же могут выполняться параллельно. При этом, вершины и ребра добавляются к графу независимо друг от друга, поэтому добавление вершин может производиться параллельно с добавлением ребер.

Проверка номеров сильно связанных компонент [8] так же может выполняться параллельно и требует [math]|n|[/math] операций ([math]n[/math] - число пар вершин, подаваемых на выход), которые так же могут выполняться параллельно.

В случае принаделжности вершин одной пары к одной сильно связанный компоненте, производится поиск в ширину [BFS], для каждой соответствующей пары. Данные поиски в ширину так же могут выполняться параллельно друг другу, при том каждый поиск в ширину имеет определенный ресурс параллелизма, описанный в соответствующем разделе.

Высота и ширина ярусно-параллельной формы зависит от структуры графа (числа и расположения сильно-связанных компонент), так как в свою очередь от нее зависит ширина и высота ЯПФ алгоритма поиска сильно-связанных компонент.

1.9 Входные и выходные данные алгоритма

Объем входных и выходных данных зависит от вариации постановки проблемы. Далее будут рассмотрены два случая.

1. Поиск полного транзитивного замыкания

Входные данные: граф [math]G(V, E)[/math], [math]|V|[/math] вершин [math]v_i[/math] и [math]|E|[/math] рёбер [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math].

Объём входных данных: [math]O(|V| + |E|)[/math].

Выходные данные: для каждой пары вершин графа её принадлежность к транзитивному замыканию.

Объём выходных данных: [math]O(|V|^2)[/math].

2. Проверка принадлежности к транзитивному замыканию для [math]n[/math] заранее заданных пар вершин [math](v_{i}, v_{j})[/math]

Входные данные: граф [math]G(V, E)[/math], [math]|V|[/math] вершин [math]v_i[/math] и [math]|E|[/math] рёбер [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math], [math]n[/math] пар вершин [math](v_{i}, v_{j})[/math].

Объём входных данных: [math]O(|V| + |E| + n)[/math].

Выходные данные: для каждой входной пары вершин её принадлежность к транзитивному замыканию.

Объём выходных данных: [math]O(n)[/math].

1.10 Свойства алгоритма

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.2.1 Локальность реализации алгоритма

2.2.1.1 Структура обращений в память и качественная оценка локальности

2.2.1.2 Количественная оценка локальности

2.3 Возможные способы и особенности параллельной реализации алгоритма

Программа, реализующая поиск транзитного замыкания, состоит CPU части, отвечающей за общую координацию вычислений, использующей вспомогательные классы.

2.4 Масштабируемость алгоритма и его реализации

2.4.1 Масштабируемость алгоритма

2.4.2 Масштабируемость реализации алгоритма

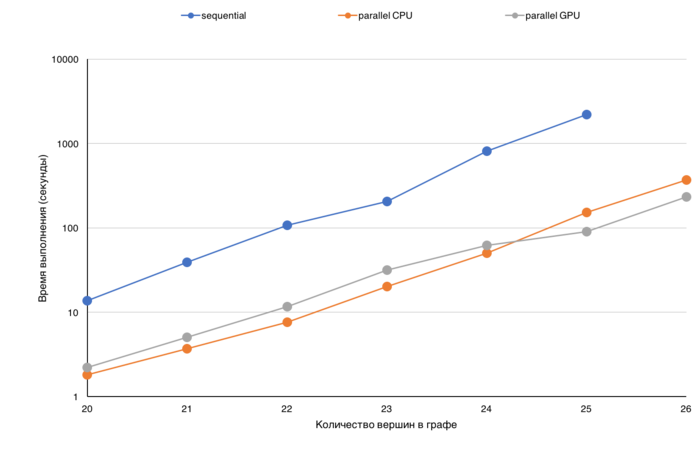
Для демонстрации эффективности представлены графики времени выполнения различных режимов вычислений в зависимости от размера входного графа.

Основной характеристикой для сравнения было выбрано время выполнения, так как производительность (определения как TEPS то есть число ребер графа, которое алгоритм обрабатывает в секунду) для данной операции не отражает реальной ситуации.

Дело в том, что сложность выбранного алгоритма Пурдома зависит от количества ребер в графе не линейно, и, кроме того, зависит еще и от структуры графа количества сильно связанных компонент).

Рисунок 2. Параллельная реализация алгоритма Пурдома масштабируемость различных версий: производительность в зависимости от размера графа.

Анализируя время выполнения можно оценить, насколько понижается эффективность обработки графа при увеличении его размера (данные перестают помещаться в кэш, в память GPU, узла и т.д.). На представленных графиках по оси X граф с каждым делением увеличивается в два раза, и по представленному графику можно оценивать, на сколько увеличилось время выполнения. Так же время выполнения можно сравнивать для различных версий, например, последовательной CPU, параллельной CPU или же GPU. На приведенной диаграмме (рисунок 1) для различных размеров графа (от 2^20 до 2^26) представлено время выполнения трех различных версий: последовательной, параллельной CPU и GPU. Шкала на данной диаграмме логарифмическая.

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Boost Graph Library (функция transitive_closure).

3 Литература

↑ Purdom, Paul, Jr. “A Transitive Closure Algorithm.” Bit 10, no. 1 (March 1970): 76–94. doi:10.1007/BF01940892.
↑ ^2,0 ^2,1 Tarjan, Robert. “Depth-First Search and Linear Graph Algorithms.” SIAM Journal on Computing 1, no. 2 (1972): 146–60.
↑ Kahn, A B. “Topological Sorting of Large Networks.” Communications of the ACM 5, no. 11 (November 1962): 558–62. doi:10.1145/368996.369025.

[Purdom-1] Purdom, Paul, Jr. “A Transitive Closure Algorithm.” Bit 10, no. 1 (March 1970): 76–94. doi:10.1007/BF01940892.

[DFS-2] 2,0 ^2,1 Tarjan, Robert. “Depth-First Search and Linear Graph Algorithms.” SIAM Journal on Computing 1, no. 2 (1972): 146–60.

[3] Kahn, A B. “Topological Sorting of Large Networks.” Communications of the ACM 5, no. 11 (November 1962): 558–62. doi:10.1145/368996.369025.

[1]

[2]

[3]

@@ Строка 27: / Строка 27: @@
 Алгоритм состоит из трех важных вычислительных частей, для каждой из которых важно оценить относительное время выполнения относительно других частей.
 # Поиск сильно связанных компонент в исходном графе
-# Построения графа промежуточного представления
+# Построение графа промежуточного представления
-# Поисков в ширину в графе промежуточного представления для построения итогового транзитивного замыкания
+# Поиски в ширину в графе промежуточного представления для построения итогового транзитивного замыкания
-. В случае решения задачи проверки принадлежности к транзитивному замыканию множество заданных пар вершин, соотношение объемов различных вычислительных частей алгоритма может быть очень различным, и, очевидно, зависит от числа пар входных вершин. Кроме того, данное соотношение может так же зависеть от типа входного графа, так как структура и количество сильно-связанных компонент сильно влияют как на время поиска сильно-связанных компонент, так и на время выполнения поисков в ширину. Далее представлена таблица, демонстрирующая процент времени выполнения данных частей для одной из реализаций алгоритма для различных типов графов с числом вершин <math>2^{23}</math>, и числом входных пар вершин для проверки равным 10000.
+. В случае решения задачи проверки принадлежности к транзитивному замыканию множества заданных пар вершин, соотношение объемов различных вычислительных частей алгоритма может быть очень различным и, очевидно, зависит от числа пар входных вершин. Кроме того, данное соотношение может также зависеть от типа входного графа, так как структура и количество сильно-связанных компонент сильно влияют как на время поиска сильно-связанных компонент, так и на время выполнения поисков в ширину. Далее представлена таблица, демонстрирующая процент времени выполнения данных частей для одной из реализаций алгоритма для различных типов графов с числом вершин <math>2^{23}</math>, и числом входных пар вершин для проверки равным 10000.
-[[file:Purdom_time_table.png|thumb|center|500px|Рисунок 1. Сравнение времни выполнения различных частей алгоритма Пурдома одной из реализаций..]]
+[[file:Purdom_time_table.png|thumb|center|500px|Рисунок 1. Сравнение времени выполнения различных частей одной из реализаций алгоритма Пурдома.]]
-Важно заметить, что некоторые алгоритмы поиска сильно-связанных компонент (например DCSC) так же основываются на поиска в ширину. Таким образом, вычислительным ядром алгоритма можно считать поиск в ширину. В свою очередь вычислительным ядром алгоритма поиска в ширину является обход вершин, смежной к выбранной вершине с последующем добавлением еще не посещенных вершин в множество "передовых" вершин.
+Важно заметить, что некоторые алгоритмы поиска сильно-связанных компонент (например, DCSC) также основываются на поисках в ширину. Таким образом, вычислительным ядром алгоритма можно считать поиск в ширину. В свою очередь вычислительным ядром алгоритма поиска в ширину является обход вершин, смежных с выбранной вершиной, с последующим добавлением еще не посещенных вершин в множество "передовых" вершин.
 . В случае решения задачи поиска полного транзитивного замыкания наиболее вычислительно затратной частью являются поиски в ширину в графе промежуточного представления, так как его необходимо произвести от всех вершин данного графа, число которых может быть значительным при большом числе сильно-связанных компонент в исходном графе.