Участник:Margarita/Градиентный спуск: различия между версиями
Margarita (обсуждение | вклад) |
Margarita (обсуждение | вклад) |
||
| Строка 103: | Строка 103: | ||
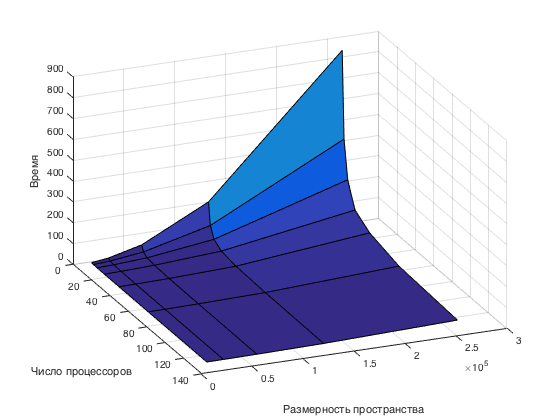
=== Масштабируемость алгоритма и его реализации === | === Масштабируемость алгоритма и его реализации === | ||
| + | |||
| + | [[file:Gradscale.png|thumb|center|700px|Рисунок 2. Масштабируемость алгоритма]] | ||
=== Динамические характеристики и эффективность реализации алгоритма === | === Динамические характеристики и эффективность реализации алгоритма === | ||
Версия 11:43, 30 ноября 2017
автор: М.В.Зайцева
Содержание
- 1 Постановка задачи
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Постановка задачи
Рассмотрим задачу поиска минимума функции f(x)\colon \mathbb{R}^n \to \mathbb{R}
- \begin{align} f(x) \rightarrow \min_{x \in \mathbb{R}^n} \end{align}
Будем считать, что у функции f(x) существуют частные производные.
Если в задаче требуется найти максимум, вместо f(x) следует брать -f(x).
1.1 Общее описание алгоритма
Градиентный спуск — это метод нахождения локального экстремума функции с помощью движения вдоль направления градиента. На каждой итерации для минимизации функции в направлении градиента используются методы одномерной оптимизации.
Градиентный спуск активно применяется в области машинного обучения, так как часть процесса машинного обучения — это поиск максимальной точности или минимизация частоты ошибок. Метод градиентного спуска используется для поиска минимальной ошибки путём минимизации функции цены.
1.2 Математическое описание алгоритма
Основная идея [1] метода состоит в том, чтобы идти в направлении антиградиента -\nabla f (отсюда название метода), то есть в направлении, в котором функция быстрее всего убывает при бесконечно малом движении из данной точки:
- \begin{align} x_{k+1} = x_{k} - \alpha_{k}\nabla f(x_{k}), \end{align}
где \alpha_{k} выбирается по одному из следующих правил:
- постоянной, в таком случае метод может не сходиться;
- дробным шагом, то есть во время итерации длина шага делится на некоторое число;
- наискорейшим спуском[2], где \alpha_{k} = \operatorname{arg}\min_{\alpha} f(x_{k} - \alpha\nabla f(x_{k})).
Таким образом идём пока не выполнится некоторый критерий останова, определяемый конкретной задачей.
1.3 Вычислительное ядро алгоритма
Наибольшая сложность алгоритма приходится на вычисление частных производных. Это особенно касается более общего случая, когда функция задана неявно и производную можно вычислить только с помощью численного дифференцирования.
1.4 Макроструктура алгоритма
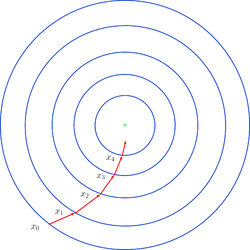
Алгоритм представляет собой итерационный процесс, на каждом шаге которого происходит вычисление последующей точки x_{k+1}. Для этого необходимо знать начальное приближение x_{0}, значение градиента в предыдущей точке \nabla f(x_{k}) и правило определения параметра \alpha_{k}, определяемое условием задачи. Кроме того, задачей определён и критерий останова, который проверяется на каждой итерации.
1.5 Схема реализации последовательного алгоритма
Алгоритм:
- Выбираем начальную точку x_{0}, \varepsilon.
- Вычисляем x_{k+1} = x_{k} - \alpha_{k}\nabla f(x_{k}), где \alpha_{k} выбирается одним из описанных выше способом.
- Если выполнено условие останова, то возвращаем x_{k+1}, иначе переходим к шагу 2.
Критерии останова могут различаться, исходя из различных соображений. Ниже приведены некоторые из них:
- \| x_{k+1} - x_{k} \| \lt \varepsilon ;
- \| f(x_{k+1}) - f(x_{k}) \| \lt \varepsilon ;
- \| \nabla f(x_{k+1}) \| \lt \varepsilon .
1.6 Последовательная сложность алгоритма
Наибольшую вычислительную сложность из арифметических операций представляют деление и умножение чисел с плавающей точкой. На каждом шаге необходимо численно вычислять производную по формуле:
- \begin{align} f'(x_0) ≈ \frac{f(x_0 + \delta) - f(x_0))}{\delta}, \end{align}
для этого потребуется n делений, где n — размерность пространства. Пусть сложность вычисления коэффициента \alpha_{k} равна p_{\alpha}. Умножение \alpha_{k} \nabla f(x_0) даёт ещё n умножений. В итоге получаем:
- \begin{align} P(n, p_{\alpha}) = 2n + p_{\alpha}. \end{align}
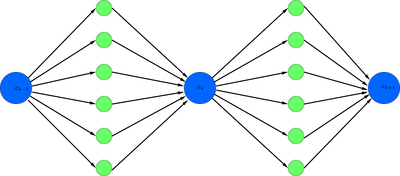
1.7 Информационный граф
Синие вершины графа — итерационное вычисление последовательности x_{k-1}, x_k, x_{k+1}.
Зелёные вершины графа — численное вычисление частных производных.
1.8 Ресурс параллелизма алгоритма
На каждой итерации алгоритма необходимо численно пересчитывать градиент функции. В случае пространства большой размерности, основная часть времени выполнения приходится на вычисление частных производных в точке, которые вычисляются независимо друг от друга.
1.9 Входные и выходные данные алгоритма
Входные данные:
- функция f(x)\colon \mathbb{R}^n \to \mathbb{R}, которая может быть задана неявно;
- начальная точка x_{0};
- правило вычисления \alpha_{k};
- критерий останова;
- точность \varepsilon.
Выходные данные:
- минимальное значение функции.
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
GitHub — реализация градиентного спуска на языке С++.
GitHub — реализация градиентного спуска на языке Java.
GitHub — реализация градиентного спуска на языке Octave.
MathWorks — реализация градиентного спуска на языке MATLAB.
Gradient descent with Python — реализация градиентного спуска на языке Python.