Участник:Svetlanalarina/Алгоритм поиска наилучшего времени регулирования для СУ 2го порядка: различия между версиями
| Строка 48: | Строка 48: | ||
Вычислительным ядром является поиск по конкретным <math> t_i \in [t_1,t_2]</math> коэффициентов и перерегулирования. Для сравнения перерегулирований возможны параллельные и не параллельные алгоритмы сортировки или поиска, пока это вопрос реализации. | Вычислительным ядром является поиск по конкретным <math> t_i \in [t_1,t_2]</math> коэффициентов и перерегулирования. Для сравнения перерегулирований возможны параллельные и не параллельные алгоритмы сортировки или поиска, пока это вопрос реализации. | ||
| − | + | == Макроструктура алгоритма === | |
Основными операциями являются нахождение <math> A_{1}, A_{2} </math> и <math> \sigma </math> (далее будем называть их парамтерами) из следующих выражений: | Основными операциями являются нахождение <math> A_{1}, A_{2} </math> и <math> \sigma </math> (далее будем называть их парамтерами) из следующих выражений: | ||
| Строка 60: | Строка 60: | ||
Так же в программе используется в функции редукции поиск минимального <math> \sigma </math> простым последовательным сравнением. | Так же в программе используется в функции редукции поиск минимального <math> \sigma </math> простым последовательным сравнением. | ||
| − | + | == Схема реализации последовательного алгоритма === | |
1) Считывание данных, а именно <math> t_{1}, t_{2}, s_1, s_2, t_{max}, cut </math>, где <math>cut</math> - количество <math> t_i</math> (разбиение); | 1) Считывание данных, а именно <math> t_{1}, t_{2}, s_1, s_2, t_{max}, cut </math>, где <math>cut</math> - количество <math> t_i</math> (разбиение); | ||
| Строка 72: | Строка 72: | ||
5) Сравнение наборов от каждого процесса с помощью функции редукции (предусмотренной в MPI), и поиск тем самым результирующего набора. Для этого необходимо описать функцию сравнений наборов параметров по <math> \sigma </math>. | 5) Сравнение наборов от каждого процесса с помощью функции редукции (предусмотренной в MPI), и поиск тем самым результирующего набора. Для этого необходимо описать функцию сравнений наборов параметров по <math> \sigma </math>. | ||
| − | + | == Последовательная сложность алгоритма === | |
Сложность вычислительного ядра можно оценить примерно следующим образом: | Сложность вычислительного ядра можно оценить примерно следующим образом: | ||
| Строка 79: | Строка 79: | ||
<math>13n </math>- арифметических операций, <math> 5n </math>- взятий экспоненты, а так же как минимум <math>n </math>сравнений. | <math>13n </math>- арифметических операций, <math> 5n </math>- взятий экспоненты, а так же как минимум <math>n </math>сравнений. | ||
| − | + | == Информационный граф === | |
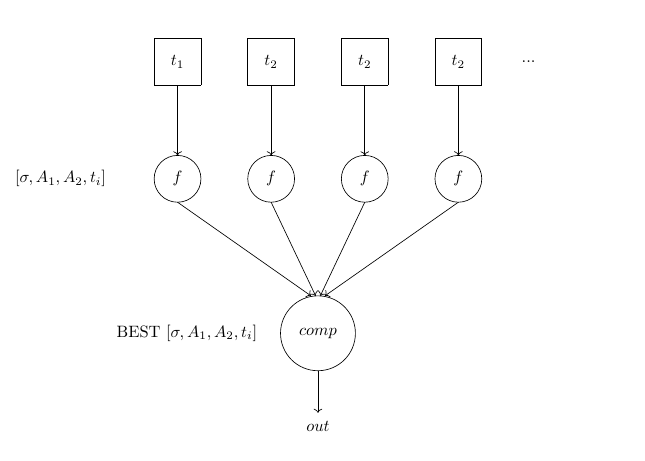
Граф алгоритма опишем аналитически и в виде рисунка. | Граф алгоритма опишем аналитически и в виде рисунка. | ||
| Строка 85: | Строка 85: | ||
[[Файл:Graph111.png]] | [[Файл:Graph111.png]] | ||
| + | |||
| + | == Ресурс параллелизма алгоритма === | ||
| + | |||
| + | В алгоритме имеются следующие шаги, как уже было сказано выше: | ||
| + | 1) Вычисление набора в функции <math> f </math>, производящееся независимо для различных точек отрезка времени на разных вычислительных узлах и выполняющееся за близкое к константному время <math> t </math>, эта операция является основной вычислительной часть алгоритма; | ||
| + | 2) Сравнение редукцией полученных наборов. | ||
| + | |||
| + | Большее время будет задействовано при редукции и сравнении наборов. Но количество сравнений всегда равно <math> (n-1) </math>. Что касается вычисления функции <math> f </math>, то оно содержит простую арифметику. Если у нас малое количество временных точек, то имеем неэффективное распараллеливание. Но при увеличении ресурсов, а именно когда каждый процесс получит по одному значению, параллелизм может быть ограничен накладными расходами. Имеем не лучше, чем константное время. | ||
| + | |||
| + | == Входные и выходные данные алгоритма === | ||
| + | |||
| + | '''Вход:''' один набор <math> t_{1}, t_{2}, s_1, s_2, t_{max}, n </math>, где <math>n</math> - количество <math> t_i</math> (разбиение); | ||
| + | |||
| + | '''Выход:''' <math> \sigma,A_1,A_2,t_{reg}</math> или само уравнение <math> e(t) = A_1e^{s1t}+A_2e^{s2t}</math> и найденные критерии качества <math> \sigma,t_{reg}</math> (для полной иллюстрации найденного процесса регулирования). | ||
= Литература = | = Литература = | ||
Версия 21:58, 1 декабря 2017
Основные авторы описания: С. Ларина (414 группа)
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма =
- 1.5 Схема реализации последовательного алгоритма =
- 1.6 Последовательная сложность алгоритма =
- 1.7 Информационный граф =
- 1.8 Ресурс параллелизма алгоритма =
- 1.9 Входные и выходные данные алгоритма =
- 2 Литература
1 Свойства и структура алгоритмов
Метод поиска времени регулирования, который будет описан и продемонстрирован имеет исключительно демонстрационный характер (демонстрация распараллеливания), но касается моей научной работы.
1.1 Общее описание алгоритма
Время регулирования является важным критерием качества в системах управления. Поэтому важен не только его поиск для конкретной системы, но и его задание, чтобы реализовывать системы с конкретными критериями качества. В моей научной работе я касаюсь этого показателя применительно к термоядерной установке токамак. Итогом алгоритма станет оптимальное для нашей системы сочетание минимального времени регулирования и минимального перерегулирования на заданном отрезке.
Для лучшего понимания объектов и терминов в данном алгоритме, стоит описать глоссарий:
[math] \Delta [/math] трубка - это линии отклонения на 5-10% от установившегося значения системы.
Время регулирования [math] t_p [/math] - это время, когда график функции, которая описывает динамическую систему, сходит в [math] \Delta [/math] трубку и более не выходит за её пределы.
Перерегулирование [math] \sigma [/math] - отклонение графика от установившегося значения, который выражается в процентах.
1.2 Математическое описание алгоритма
Для системы управления 2-го порядка поиск времени регулирования может быть найден из следующих уравнений
- [math] \begin{cases} \Delta = A_1e^{s_1 t_p}+A_2e^{s_2 t_p}, \\ A_1+A_2=1. \end{cases} [/math],
где заданы полюса [math] s_1 \lt s_2 \lt 0 [/math] и известно [math] \Delta [/math].
Мой алгоритм поиска [math] t_p [/math] заключается в том, что я задаю конкретный диапазон, в который должно входить мое время [math] t_p \in [t_1,t_2][/math]. Затем для каждого [math] t_i \in [t_1,t_2][/math] производится подбор соответствующих [math] A_1 [/math] и [math] A_2 [/math] с помощью уравнений описанных выше. Эти коэффициенты нужны для подстановки в следующее выражение на перерегулирование [math] \sigma [/math]:
- [math] \sigma = e_{max} \cdot 100 \%, \\ e_{max} = A_1e^{s_1 t_{max}}+A_2e^{s_2 t_{max}}. [/math]
Для [math] n [/math] различных [math] t_i [/math] на отрезке будем находить перерегулирования [math] \sigma_i [/math], а так же сохранять соответствующие ему коэффициенты [math] A_{1,i}, A_{2,i} [/math] и непосредственно само значение [math] t_i [/math].
Сравнивая [math] \sigma_i [/math], находим наименьшее из них. Таким образом, получим результат алгоритма: минимальное время регулирования и минимальное перерегулирование.
1.3 Вычислительное ядро алгоритма
Вычислительным ядром является поиск по конкретным [math] t_i \in [t_1,t_2][/math] коэффициентов и перерегулирования. Для сравнения перерегулирований возможны параллельные и не параллельные алгоритмы сортировки или поиска, пока это вопрос реализации.
1.4 Макроструктура алгоритма =
Основными операциями являются нахождение [math] A_{1}, A_{2} [/math] и [math] \sigma [/math] (далее будем называть их парамтерами) из следующих выражений:
- [math] A_1 = \dfrac{\Delta - e^{s_2 t_p}}{e^{s_1 t_p} - e^{s_2 t_p}}\\ A_2=1-A1, \\ \sigma = A_1e^{s_1 t_{max}}+A_2e^{s_2 t_{max}} \cdot 100 \%. [/math]
Так же в программе используется в функции редукции поиск минимального [math] \sigma [/math] простым последовательным сравнением.
1.5 Схема реализации последовательного алгоритма =
1) Считывание данных, а именно [math] t_{1}, t_{2}, s_1, s_2, t_{max}, cut [/math], где [math]cut[/math] - количество [math] t_i[/math] (разбиение);
2) Разделение необходимого числа [math] t_i [/math] между процессами;
3) Вычисление всеми процессами [math] A_{1}, A_{2} [/math] и [math] \sigma [/math] на каждом [math] t_i [/math] (описано в макроструктуре);
4) Поиск в цикле наилучшего набора параметров;
5) Сравнение наборов от каждого процесса с помощью функции редукции (предусмотренной в MPI), и поиск тем самым результирующего набора. Для этого необходимо описать функцию сравнений наборов параметров по [math] \sigma [/math].
1.6 Последовательная сложность алгоритма =
Сложность вычислительного ядра можно оценить примерно следующим образом: Для разбиения n понадобится:
[math]13n [/math]- арифметических операций, [math] 5n [/math]- взятий экспоненты, а так же как минимум [math]n [/math]сравнений.
1.7 Информационный граф =
Граф алгоритма опишем аналитически и в виде рисунка.
Вершины это начальные данные [math] t_i [/math], которые разнятся от процесса к процессу. Далее в вершинах функции [math] f [/math], осуществляющие поиск по [math] t_i [/math] набора [math] [\sigma,A_1,A_2,t_i][/math], которых существует блоком для передачи в результат. Затем от функции [math] f [/math] наборы переходят на операцию сравнения наборов по параметру [math] \sigma[/math]. В качестве результата получаем удовлетворяющий нас набор.
1.8 Ресурс параллелизма алгоритма =
В алгоритме имеются следующие шаги, как уже было сказано выше: 1) Вычисление набора в функции [math] f [/math], производящееся независимо для различных точек отрезка времени на разных вычислительных узлах и выполняющееся за близкое к константному время [math] t [/math], эта операция является основной вычислительной часть алгоритма; 2) Сравнение редукцией полученных наборов.
Большее время будет задействовано при редукции и сравнении наборов. Но количество сравнений всегда равно [math] (n-1) [/math]. Что касается вычисления функции [math] f [/math], то оно содержит простую арифметику. Если у нас малое количество временных точек, то имеем неэффективное распараллеливание. Но при увеличении ресурсов, а именно когда каждый процесс получит по одному значению, параллелизм может быть ограничен накладными расходами. Имеем не лучше, чем константное время.
1.9 Входные и выходные данные алгоритма =
Вход: один набор [math] t_{1}, t_{2}, s_1, s_2, t_{max}, n [/math], где [math]n[/math] - количество [math] t_i[/math] (разбиение);
Выход: [math] \sigma,A_1,A_2,t_{reg}[/math] или само уравнение [math] e(t) = A_1e^{s1t}+A_2e^{s2t}[/math] и найденные критерии качества [math] \sigma,t_{reg}[/math] (для полной иллюстрации найденного процесса регулирования).
2 Литература
Ким Д.П. - Теория автоматического управления. Том 1. Линейные системы - 2003;
Ким Д.П. - Теория автоматического управления. Том 2. Линейные системы - 2004.