Участник:PopovaElizaveta/Метод Гаусса приведения матрицы к верхнему треугольному виду: различия между версиями
| Строка 152: | Строка 152: | ||
===== Масштабируемость реализации ===== | ===== Масштабируемость реализации ===== | ||
| − | Проведем исследование масштабируемости параллельной реализации алгоритма на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета. Используемый компилятор: icc version 15.0.0 (gcc version 4.4.7 compatibility). Исследуемая программа написана на языке C с использованием библиотеки MPI и стандартных библиотек | + | Проведем исследование масштабируемости параллельной реализации алгоритма на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета. Используемый компилятор: icc version 15.0.0 (gcc version 4.4.7 compatibility). Исследуемая программа написана на языке C с использованием библиотеки MPI и стандартных библиотек языка C. |
Значения изменяемых параметров запуска: | Значения изменяемых параметров запуска: | ||
Текущая версия на 21:04, 3 декабря 2017
Автор описания: Попова Елизавета
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Метод Гаусса приведения матрицы к верхнему треугольному виду - часть (прямой ход) метода Гаусса решения систем линейных алгебраических уравнений и нахождения обратных матриц. Применения только прямого хода достаточно для подсчета ранга матриц. Метода Гаусса приведения матрицы к верхнему треугольному виду состоит в последовательном исключении элементов матрицы, стоящих под главной диагональю, с помощью элементарных преобразований. Вначале среди элементов превого столбца матрицы выбирают ненулевой, далее путем перестановки строк помещают его на крайнее верхнее положение. Полученную после перестановки первую строку домножают на число, обратное к первому элементу этой строки. Таким образом, элемент в первом столбце первой строки становится равным единице. После этого первую строку вычитают из всех последующих, домножая ее на число, равное первому элементу каждой из этих строк. Таким образом, "зануляются" все элементы первого столбца матрицы кроме того, который находится в первой строке. После данных преобразований первая строка и первый столбец исходной матрицы "вычеркиваются" из рассмотрения, и аналогичные преобразования применяются к полученной после "вычеркивания" матрице до тех пор, пока не останется матрица нулевого размера. Если на каком-то шаге среди элементов первого столбца не найдено ненулевого, то переходят к следующему столбцу и проделывают аналогичные операции.
1.2 Математическое описание алгоритма
Исходные данные: вещественная матрица [math] A [/math] (элементы [math] a_{ij}[/math]).
Вычисляемые данные: верхняя треугольная матрица [math] U [/math].
В прямом ходе метода Гаусса элементы матрицы [math] A [/math] преобразуются по следующему правилу:
[math] a_{kj}^{(0)} = a_{kj}, \qquad k,j = 1, 2, \ldots, m, [/math]
[math] c_{kj} = {a_{kj}^{(k-1)} \over {a_{kk}^{(k-1)}}}, \qquad j = k+1, k+2, \ldots ,m, \quad k = 1, 2, \ldots, m. [/math]
[math] a_{ij}^{(k)} = a_{ij}^{(k-1)} - a_{ik}^{(k-1)}c_{kj}, \qquad i,j = k+1, k+2, \ldots, m, \quad k = 1, 2, \ldots, m-1. [/math]
Основным ограничением метода является предположение, что все элементы [math] a_{kk}^{(k-1)}[/math], на которые проводится деление, отличны от нуля. Число [math] a_{kk}^{(k-1)}[/math] называется ведущим элементом на [math] k-[/math]ом шаге исключения.
Для [math] \quad k = 1, 2 \ldots m, \quad j = k+1, k+2 \ldots m [/math] элементы верхней треугольной матрицы получаются следующим образом:
[math] u_{kj} = a_{kj}^{(k-1)}. [/math]
1.3 Вычислительное ядро алгоритма
Вычислительное ядро метода Гаусса можно составить из множественных (всего их [math] {m(m-1)} \over {2} [/math] ) вычислений отношений
[math] c_{kj} = {a_{kj}^{(k-1)} \over {a_{kk}^{(k-1)}}}[/math]
в режиме накопления или без него, в зависимости от требований задачи, и дальнейших вычислений (всего их [math] {(m-1)m(2m-1)} \over {6} [/math] ) элементов [math] a_{ij}^{(k)} [/math] по формуле
[math] a_{ij}^{(k-1)} - a_{ik}^{(k-1)}c_{kj} [/math]
1.4 Макроструктура алгоритма
Метод Гаусса приведения матрицы к верхнему треугольному виду состоит из [math] m-1 [/math] шага, на каждом из которых выполняются следующие операции:
- Все элементы ведущей строки [math] k[/math]-го шага делятся на ненулевой элемент этой строки, расположенный в аннулируемом на данном шаге ([math] k[/math]-ом) столбце.
- Далее из каждой строки матрицы, начиная с [math] k+1 [/math]-ой, вычитается преобразованная в пункте 1 ведущая строка, умноженная на элемент текущей обрабатываемой строки, расположенный в аннулируемом ([math] k[/math]-ом) столбце.
1.5 Схема реализации последовательного алгоритма
Последовательные шаги описываемого алгоритма имеют следующий вид:
[math]1. \quad a_{kj}^{(0)} = a_{kj} , \quad где \quad k, j = 1,2, \ldots, m [/math]
Далее для всех [math] k = 1, 2, \ldots, m - 1 [/math] вычисляются следующие значения
[math] 2. \quad u_{kj} = a_{kj}^{(k-1)}, \qquad j = k, k+1, k+2, \ldots ,m. [/math]
[math] 3. \quad c_{kj} = {a_{kj}^{(k-1)} \over {a_{kk}^{(k-1)}}}, \qquad j = k+1, k+2, \ldots ,m. \\ a_{ij}^{(k)} = a_{ij}^{(k-1)} - a_{ik}^{(k-1)}c_{kj}, \qquad i,j = k+1, k+2, \ldots, m. [/math]
Отметим, что вычисления [math] a_{ij}^{(k)} [/math] могут происходить в режиме накопления, в зависимости от условий задачи.
1.6 Последовательная сложность алгоритма
Вычисление ненулевых элементов [math] u_{ij} [/math] треугольной матрицы [math] U [/math] требует:
- по [math]\frac{m(m-1)}{2} [/math] операций деления
- по [math] {{(m-1)m(2m-1)} \over {6}} [/math] опреаций умножения и вычитания
Выполнение операций умножения и деления составляет основную часть алгоритма.
Таким образом, при больших [math] m [/math] число действий [math] \approx {{m^3} \over {3}} [/math].
1.7 Информационный граф
Граф метода Гаусса приведения матрицы к верхнему треугольному виду состоит из трех групп вершин, расположенных в целочисленных узлах трех областей разной размерности.
Первая группа вершин расположена в одномерной области, ей соответствует операция обращения входного элемента. Естественно введенная единственная координата каждой из вершин [math] i [/math] изменяется от [math] 1 [/math] до [math] m - 1 [/math]. Входной элемент в этой операции:
- при [math] i = 1 [/math] - элемент исходной матрицы [math] a_{11} [/math].
- при [math] i \gt 1 [/math] - результат срабатывания операции, соответствующей вершине из третьей группы, с координатами [math] i-1, i, i [/math]
Результат срабатывания операции является промежуточным данным алгоритма.
Вторая группа вершин расположена в двумерной области, ей соответствует операция умножения [math] ab [/math]. Естественно введенные координаты области:
- [math] i [/math] меняется в диапазоне от [math] 1 [/math] до [math] m. [/math]
- [math] j [/math] меняется в диапазоне от [math] i+1 [/math] до [math] m.[/math]
Аргументы операции:
- [math] a: [/math]
- при [math] i = 1 [/math] - элемент исходной матрицы [math] a_{1j} [/math]
- при [math] i \gt 1 [/math] - результат выполнения операции, соответствующей вершине из третьей группы с координатами [math] i, j. [/math]
- [math] b: [/math] - результат выполнения операции, соответствующей вершине из первой группы с координатой [math] i. [/math]
Результат срабатывания операции является промежуточным данным алгоритма.
Третья группа вершин расположена в трехмерной области, ей соответствует операция [math] a - bc. [/math] Естественно введенные координаты области:
- [math] k [/math] меняется в диапазоне от [math] 1 [/math] до [math] m - 1. [/math]
- [math] i [/math] меняется в диапазоне от [math] k+1 [/math] до [math] m. [/math]
- [math] j [/math] меняется в диапазоне от [math] k+1 [/math] до [math] m. [/math]
Аргументы операции:
- [math] a: [/math]
- при [math] k = 1 [/math] - элемент исходной матрицы [math] a_{ij} [/math]
- при [math] k \gt 1 [/math] - результат выполнения операции, соответствующей вершине из третьей группы с координатами [math] k - 1, i, j. [/math]
- [math] b: [/math]
- при [math] k = 1 [/math] - элемент исходной матрицы [math] a_{i1} [/math]
- при [math] k \gt 1 [/math] - результат выполнения операции, соответствующей вершине из третьей группы с координатами [math] k - 1, i, k. [/math]
- [math] c: [/math] - результат выполнения операции, соответствующей вершине из второй группы с координатами [math] k, j [/math]
Результат срабатывания операции является выходным данным [math] u_{(k+1)j}. [/math]
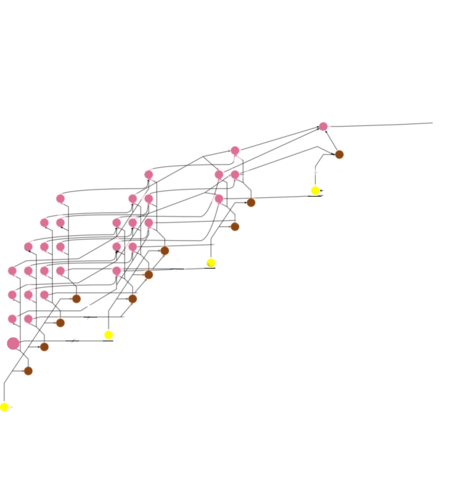
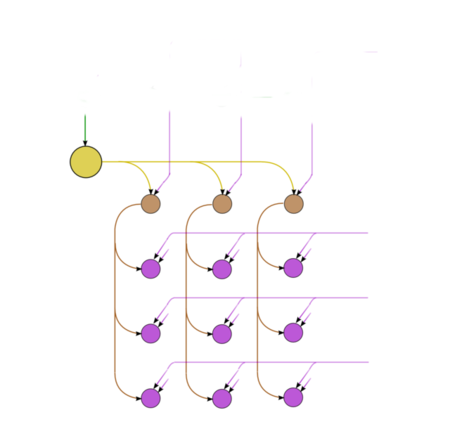
Описанный граф представлен на рис.1, выполненном для случая [math] n = 5. [/math] Здесь вершины первой группы обозначены желтым цветом, вершины второй группы - коричневым, вершины третьей группы - фиолетовым. На рис.2 изображен один шаг метода Гаусса.
1.8 Ресурс параллелизма алгоритма
Для метода Гаусса в случае квадратной матрицы размера [math] m [/math] в параллельном варианте требуется последовательно выполнить следующие ярусы:
- [math] m - 1 [/math] ярусов обращения (в каждом из ярусов одно обращение)
- [math] m - 1 [/math] ярусов умножения (в каждом ярусе от [math] 1 [/math] до [math] m-1 [/math] умножения)
- [math] m - 1 [/math] ярусов умножения и сложения/вычитания (в каждом ярусе от [math] 1 [/math] до [math] {m(m-1)} \over {2} [/math] операций)
Таким образом, при классификации по высоте ЯПФ, метод Гаусса приведения матрицы к верхнему треугольному виду относится к алгоритмам с линейной сложностью. При классификации по ширине ЯПФ его сложность будет квадратичной.
1.9 Входные и выходные данные алгоритма
Входные данные: вещественная матрица [math] A [/math] (элементы [math] a_{ij} [/math] ).
Объем входных данных: [math] m^2 [/math], где [math] m [/math] - размер исходной матрицы [math] A. [/math]
Выходные данные: верхняя треугольная матрица [math] U[/math] (элементы [math] u_{ij} [/math]).
Объем выходных данных: [math] {m(m+1)} \over {2} [/math] (в силу треугольности выходной матрицы достаточно хранить только диагональные и наддиагональные элементы матрицы [math] U [/math]).
2 Программная реализация алгоритма
2.1
2.2
2.3
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
В параллельном алгоритме метода Гаусса процессы ищут возможную опорную строку среди своих непомеченных строк, затем корневой процесс выбирает процесс, который будет рассылать опорную строку. Распараллеливание данной работы происходит путем разделения строк исходной матрицы [math] A [/math] между процессами. Поэтому увеличение числа процессов возможно лишь до тех пор, пока количество процессов на превосходит количества строк матрицы. Дальнейшее увеличение числа процессов бессмысленно.
2.4.2 Масштабируемость реализации
Проведем исследование масштабируемости параллельной реализации алгоритма на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета. Используемый компилятор: icc version 15.0.0 (gcc version 4.4.7 compatibility). Исследуемая программа написана на языке C с использованием библиотеки MPI и стандартных библиотек языка C.
Значения изменяемых параметров запуска:
- число процессов [8,16,32,64,128]
- размер матрицы [128,256,384,512]
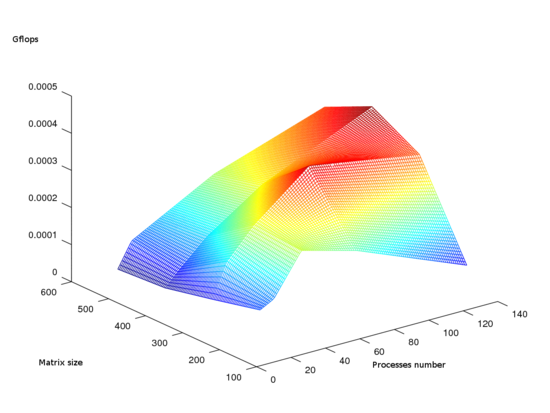
На следующем рисунке приведен график производительности выбранной реализации алгоритма в зависимости от входных параметров.
На графике видно, что для одного и того же размера матрицы производительность с увеличением числа процессов в начале увеличивается, а затем начинает падать. То есть в какой-то момент затраты на пересылку данных между процессами превышают эффект ускорения при распараллеливании алгоритма.
2.5
2.6
2.7 Существующие реализации алгоритма
Описанный выше метод Гаусса реализован в большинстве алгебраических библиотек, в том числе LAPACK, ScaLAPACK, Armadillo (C++ linear algebra library) и др, однако не в чистом виде, а в составе алгоритма LU-разложения матрицы. Данный алгоритм является одной из разновидностей метода Гаусса, он позволяет получать представление исходной матрицы [math] A [/math] в виде произведения нижней треугольной и верхней треугольной матриц.
Приведенные примеры библиотек являеются свободно распространяемыми.
3 Литература
1. А.А. Самарский, А.В. Гулин. Численные методы. М.: Наука 1989
2. В.А. Ильин, Г.Д. Ким. Линейная алгебра и аналитическая геометрия