Участник:Noite/EM-алгоритм кластеризации

EM-алгоритм кластеризации
Последовательный алгоритм
Последовательная сложность	[math]O(n * m^2 * k)[/math] - одна итерация
Объём входных данных	[math]n * m + 1[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math][/math]
Ширина ярусно-параллельной формы	[math][/math]

Автор описания: Зинченко Д.А.

Алгоритм кластеризации, основанный на максимизации ожидания (EM-алгоритм)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

В задачах оптимизации EM-алгоритмом называют итеративную процедуру поиска численного значения экстремума какой-либо функции. В частности, в статистике этот алгоритм используется для оценки максимального правдоподобия. Впервые название EM-алгоритм было предложено в 1977 году, однако его идеи были описаны и раньше.

EM-алгоритм применяется для решения задач двух типов :

1. Анализ неполных данных (данных с пропусками).
2. Оценка максимального правдоподобия в случае, если функцию правдоподобия трудно исследовать аналитически. В этом случае введение набора скрытых переменных может существенно упростить задачу.

Задача кластеризации относится к задачам второго типа. В данной статье рассматривается следующая постановка задачи кластеризации:

Дано множество объектов, каждый из которых представляет собой точку в n-мерном метрическом пространстве. Каждому измерению пространства соответствует некоторое свойство объекта. Необходимо разбить это множество на k подмножеств так, чтобы, чтобы элементы каждого подмножества существенно отличались по свойствам от элементов других подмножеств.

Использование алгоритма EM подразумевает следующее предположение об объектах:

Пусть объекты, которые необходимо разбить на кластеры, появляются случайным образом и независимо друг от друга согласно вероятностному распределению, равному смеси (линейной комбинации) распределений кластеров. В данной статье в дальнейшем будет считаться, что распределение каждого кластера является многомерным нормальным распределением с произвольной матрицей ковариации - наиболее часто используемое предположение.

Тогда каждый объект принадлежит каждому кластеру, но с разной вероятностью. EM-алгоритм итеративно оценивает параметры распределений кластеров, максимизируя логарифмическую функцию максимального правдоподобия. После окончания работы алгоритма объект будет отнесен к кластеру, вероятность принадлежности которому максимальна. Вводимый набор скрытых переменных для каждого объекта - вероятности того, что объект принадлежит каждому из кластеров.

Итерация алгоритма состоит из двух последовательных шагов.

1. (Expectation) Вычисляются новые ожидаемые значения скрытых переменных.
2. (Maximization) Решается задача максимизации правдоподобия: По текущим значениям скрытых переменных обновляются параметры распределений для кластеров: математическое ожидание, дисперсия и вероятность появления объектов из кластера.

1.2 Математическое описание алгоритма

Используемые обозначения:

[math]N[/math] - количество объектов, [math]K[/math] - количество кластеров, [math]M[/math] - количество параметров объекта

[math]\gamma_{n,k}[/math] - значения скрытых переменных

[math]N_{k}[/math] - количество элементов отнесенных к соответствующему кластеру

[math]x_{1},...,x_n[/math] - объекты

Параметры распределений:

[math]w_{1},...,w_{k}[/math] - вероятности появления объектов из кластеров (веса кластеров), [math]\sum_{k=1}^Kw_{k}=1[/math]

[math]\mu_{1},...,\mu_{k}[/math] - центры гауссиан кластеров

[math]\Sigma_{1},...,\Sigma_{k}[/math] - матрицы ковариации гауссиан кластеров, каждая матрица имеет размерность [math]M[/math]x[math]M[/math]

Смесь распределений:

[math] P(x) = \sum_{j=1}^Kw_jp(x|\mu_{j}, \Sigma_{j})[/math]

Цель алгоритма - вычислить параметры распределений, максимизирующих логарифм функции правдоподобия:

[math]\ln P(x|w,\mu,\Sigma)= \sum_{n=1}^N \ln \{ \sum_{k=1}^K w_{k}p(x_{n}|\mu_{k},\Sigma_{k})\}[/math].

• В начале работы алгоритма задаются параметры начального приближения:

[math]w_{i} = 1/K, \mu_{i} = random(x_{j}), i=1..K, j=1..N[/math] [math]\Sigma_{j,j}^{k}=\frac{1}{NK}\sum_{i=1}^N(x_{i,j} - \mu_{k,j})^2, k=1..K, j=1..M[/math]

Поскольку от начального приближения может сильно зависеть результат работы алгоритма, вместо инициализации кластеров случайными центрами, равными весами и диагональными матрицами ковариации, как в приведенных формулах, часто применяют другие способы (подробнее - в особенностях реализации)

• Далее итеративно выполняется следующая пара процедур:
  • E-шаг: используя текущее значение параметров [math]w_{1},...,w_{k};\mu_{1},...,\mu_{k};\Sigma^{1},...,\Sigma^{k}[/math], вычисляем значение вектора скрытых переменных [math]\gamma[/math]:[math]\gamma_{n,k}=\frac{w_{k}p(x_{n}|\mu_{k},\Sigma^{k})}{\sum_{j=1}^K w_{j}p(x_{n}|\mu_{j},\Sigma^{j})}, [/math] знаменатель дроби - нормировочный коэффициент[math]p(x|\mu,\Sigma)=\frac{1}{{(2\pi)}^{\frac{N}{2}}\sqrt{|\Sigma|}}exp\biggl\{-\frac{1}{2}{(x-\mu)}^T{\Sigma}^{-1}(x-\mu)\biggr\}[/math] - плотность [math]N[/math]-мерного нормального распределения
  • М-шаг: переоценка параметров по текущим значениям скрытых переменных для [math]k = 1..K[/math]:

[math]\mu^{new}_{k}=\frac{1}{N_{k}}\sum_{n=1}^N \gamma_{n,k}x_{n}[/math], [math]\Sigma_{new}^{k}=\frac{1}{N_{k}}\sum_{n=1}^N \gamma_{n,k} (x_{n}-\mu_{k}^{new})(x_{n}-\mu_{k}^{new})^{T}[/math], [math]w_{k}^{new}=\frac{N_{k}}{N}[/math], [math]N_{k}=\sum_{n=1}^N \gamma_{n,k}[/math].

В EM алгоритме используется один из следующих критериев остановки:

• Норма разности векторов скрытых переменных на текущей итерации не превышает заданную константу
• Прошествие заданного количества итераций
• Изменение логарифмического правдоподобия меньше заданной константы.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма состоит из двух шагов, повторяющихся каждую итерацию:

• Обновление скрытых переменных на основе текущих параметров распределений
• Обновление параметров кластеров: весов, центров и матриц ковариации

1.4 Макроструктура алгоритма

Как записано в описании вычислительного ядра алгоритма, основную часть алгоритма составляют итеративно проводимые макрооперации: Expectation шаг - вычисление новых значений скрытых переменных, Maximization шаг - обновление параметров кластеров. Макроструктура алгоритма представлена на рисунке 1:

Рисунок 1: Макроструктура EM-алгоритма

1.5 Схема реализации последовательного алгоритма

Примерная схема реализации EM алгоритма с предварительной обработкой матриц ковариации:

// n - количество объектов

// m - количество координат объектов

// k - количество кластеров

Инициализировать веса и центры кластеров;
Инициализировать матрицы ковариации;

// Основной цикл
Пока условие остановки не выполнено
    // E-шаг
    В цикле для каждого кластера
        Вычислить определитель матрицы ковариации Sigma;
        Вычислить обратную матрицу матрице Sigma;
    В цикле для каждого объекта
        В цикле для каждого кластера
            Вычислить и запомнить p(x | mu, Sigma) для текущего объекта и кластера;
            Просуммировать вычисленные p(x | mu, Sigma);
        В цикле для каждого кластера
            Обновить скрытые переменные gamma;
    // M-шаг
    Обновить веса w;
    Обновить центры кластеров mu;
    Обновить матрицы ковариации Sigma;

1.6 Последовательная сложность алгоритма

Количество итераций алгоритма зависит от условия остановки, поэтому будем рассматривать сложность одной итерации.

Шаг E

Сложность вычисления определителя произвольной матрицы ковариации [math]\Sigma[/math] методом Гаусса - [math]O(m^3)[/math];

Сложность вычисления матрицы, обратной произвольной матрице ковариации [math]\Sigma[/math] методом Гаусса - [math]O(m^3)[/math];

Сложность предварительного вычисления определителей и обратных матриц матрицам ковариации - [math]O(k * m^3)[/math]

С учетом заранее вычисленных определителей и обратных матриц сложность вычисления [math]p(x | \mu,\Sigma)[/math] составит: [math]O(m^2)[/math];

Суммарно сложность шага E составит [math]O(n * m^2 * k + k * m^3)[/math]

Шаг M

Сложность обновления весов кластеров [math]O(k * n)[/math];

Сложность обновления центров кластеров [math]O(k * m * n)[/math];

Сложность обновления одной матрицы ковариации [math]O(n * m)[/math];

Сложность обновления всех матриц ковариации [math]O(k * m * n)[/math];

Суммарно сложность шага M алгоритма - [math]O(k * m * n)[/math];

Таким образом, сложность одной итерации EM алгоритма для псевдокода, указанного в предыдущем разделе, составит [math]O(k * m^2 * n + k * m^3 + k * m * n)[/math].

В предположении, что размерность объектов много меньше их количества [math]m \lt \lt n[/math] получим сложность итерации [math]O(k * m^2 * n)[/math].

Нетрудно заметить, что вычисление определителя и обратной матрицы к произвольной матрице ковариации составляет большУю часть работы шага E и существенно влияет на его сложность. Поэтому эти вычисления проведены заранее - вынесены за основной цикл шага E. Помимо этого сложность этих вычислений можно сократить еще сильнее, если ввести ограничения структуру матрицы ковариации [math]\Sigma[/math].

Наиболее часто используемым ограничением, позволяющим эффективно распараллеливать алгоритм, является предположение, что матрица ковариации имеет диагональную форму. Тогда вычисление её определителя и обратной матрицы имеет сложнось [math]O(m)[/math], а суммарная сложность шага E и сложность всей итерации составит [math]O(k * m * n)[/math].

1.7 Информационный граф

Макроструктура алгоритма представлена на рисунке 1 (см. раздел 1.4 статьи).

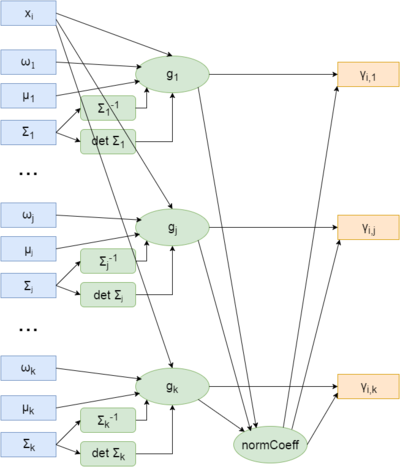
На рисунке 2 представлена схема вычислений E-шага алгоритма для одного объекта: для объекта [math]x_{i}[/math] и параметров [math]w_{j}, \mu_{j}, \Sigma_{j}, j=1..k[/math] по формулам раздела 1.2 вычисляются ненормированные значения скрытых переменных [math]g_{j}[/math], нормировочный коэффициент normСoeff, и получаются итоговые значения [math]\gamma_{i,j}[/math].

Рисунок 2: E-шаг EM алгоритма для одного объекта

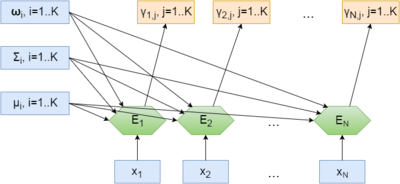
На рисунке 3 представлена схема вычислений E-шага алгоритма для всех объектов: для объекта [math]x_{j}[/math] и параметров-векторов [math]w, \mu, \Sigma[/math] по формулам раздела 1.2 вычисляются значения скрытых переменных. [math]E_{i}, i=1..n[/math] - маркооперации, E-шаги для соответствующих объектов.

Рисунок 3: E-шаг EM алгоритма для всех объектов

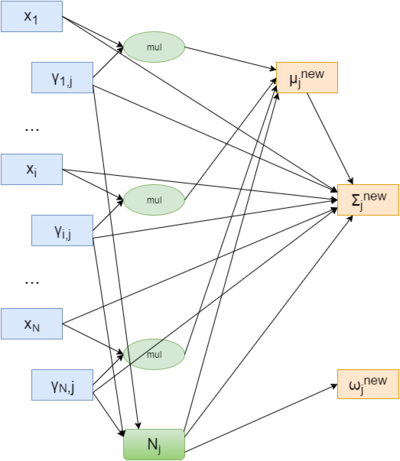
На рисунке 4 представлена схема вычислений M-шага алгоритма для одного кластера: для объектов [math]x_{i}[/math] и скрытых переменных [math]\gamma_{i,j}[/math], соответствующих степени принадлежности этих объектов кластеру [math]j[/math], согласно формулам шага M раздела 1.2 вычисляется нормировочный коэффициент [math]N_{j}[/math] и параметры этого кластера: вес [math]w_{j}^{new}[/math], матрица ковариации [math]\Sigma_{j}^{new}[/math] и центр кластера [math]\mu_{j}^{new}[/math].

Рисунок 4: M-шаг EM алгоритма для одного кластера

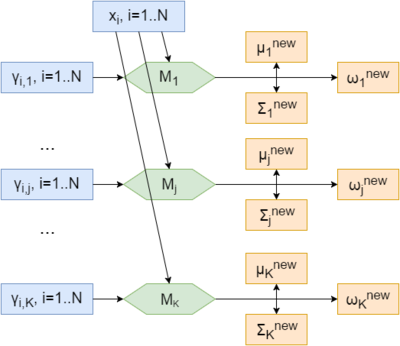
На рисунке 5 представлена схема вычислений M-шага алгоритма для всех кластеров. [math]M_{j}, j=1..k[/math] соответствует макрооперации - M-шагу для соответствующего кластера и скрытых переменных.

Рисунок 5: M-шаг EM алгоритма для всех кластеров

1.8 Ресурс параллелизма алгоритма

Из схем вычислений шагов E и M шагов алгоритма, приведенным в предыдущем разделе, видно, что если размерность матрицы ковариации небольшая (тогда вычисление определителя и обратной матрицы матрице ковариации не является трудоемкой операцией), обе макрооперации EM алгоритма можно распараллеливать как по кластерам, так и по объектам.

Как правило количество кластеров, на которые нужно разбить объекты, несравнимо меньше количества объектов, поэтому распараллеливание в большинстве существующих реализаций происходит по объектам: обработка объектов по возможности равномерно распределяются по кластерам. Теоретически (если считать передачу данных между процессорами мгновенной) при наличии неограниченного числа процессоров сложность алгоритма составит [math]O(m^2 * k)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные:

• Целое неотрицательное число [math]k[/math] - количество кластеров;
• Значения координат объектов [math]x_{i}[/math] - [math]n[/math] объектов с [math]m[/math] координатами каждый.

Объем входных данных:

• [math]n * m[/math] вещественных чисел (если координаты объектов - вещественные числа), [math]1[/math] целое неотрицательное число.

Выходные данные:

• Вектор длины [math]n[/math] - для каждого объекта указан номер кластера, к которому он отнесен.

Объем выходных данных:

• [math]n[/math] целых неотрицательных чисел.

1.10 Свойства алгоритма

1.10.1 Преимущества и недостатки

EM-алгоритм обладает следующими преимуществами и недостатками:

Преимущества:

1. Слабо чувствителен к выбросам
2. Прост в реализации
3. Быстро сходится при удачном выборе начальных значений параметров.

Недостатки:

1. Неустойчив к выбору начальных значений параметров - от них зависит как скорость сходимости, так и результат работы: алгоритм может сойтись к локальному экстремуму функции правдоподобия, который может быть существенно ниже глобального.
2. Алгоритм не находит оптимальное количество кластеров. Количество кластеров, на которые нужно разбить множество объектов, является параметром алгоритма.
3. При большой размерности пространства объектов выдвинутое предположение о модели их распределения может быть некорректным.

1.10.2 Влияние структуры матрицы ковариации на форму кластера

Рисунок 6: Влияние структуры матрицы ковариации на форму кластеров для двумерного случая. a) - матрицы ковариации являются диагональными, b) - матрицы ковариации произвольны.

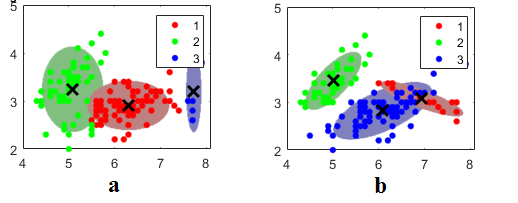
Рисунок 6 наглядно показывает, что при диагональной форме матриц ковариации полуоси эллипса (в общем случае - эллипсоида), соответствующего распределению объектов, отнесенных кластеру, параллельны осям координат объектов. В противном случае полуоси могут располагаться произвольным образом.

1.10.3 Общие свойства

Вычислительная мощность EM алгоритма равна [math]m * k * it[/math], где [math]m[/math] - размерность объекта, [math]k[/math] - количество кластеров, а [math]it[/math] - количество итераций.

EM-алгоритм является итерационным, и число итераций в общем случае не фиксировано: оно зависит от условий остановки, начальных приближений и расположения объектов. Поэтому этот алгоритм недетерминированный. По тем же причинам EM-алгоритм является неустойчивым.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

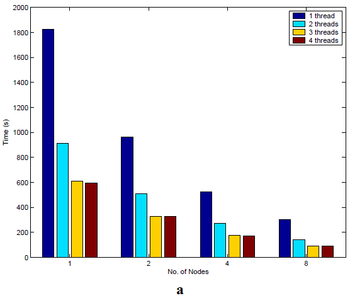
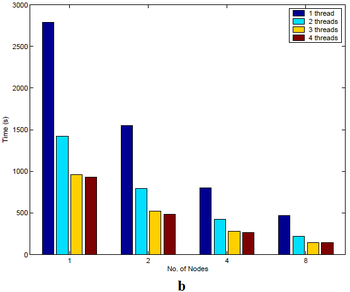
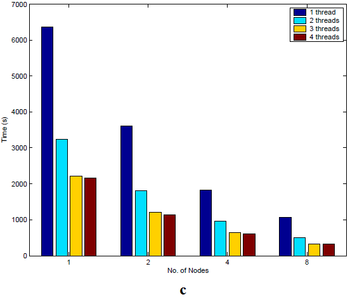
Многие статьи, в которых представлены параллельные реализации EM алгоритма, описывают помимо использующихся программных и аппаратных решений результаты проведенных экспериментов с данными. В качестве примера в этом разделе будут рассмотрены результаты эксперементов, проведенных со связующим программным обеспечением (middleware) FREERIDE (FRamework for Rapid Implementation of Datamining Engines), обеспечивающим возможность распараллеливания как для систем с общей памятью (в частности, симметричных мультипроцессорных систем), так и для систем с распределенной памятью.

Эксперименты проводились на кластере машин Pentium 700MHz связанных при помощи Myrinet LANai 7.0 на трех наборах данных:

а) 3.3 * 10^6 объектов

b) 6.2 * 10^6 объектов

c) 12.5 * 10^6 объектов

Объекты представляют собой координаты точек 10-мерного пространства.

Количество машин в кластере варьировалось от 1 до 8, при этом на каждой машине запускалось до четырех параллельных потоков.

Результаты экспериментов представлены на рисунках 7-9 (источник - [9]):

Рисунок 7: набор данных a)

Рисунок 8: набор данных b)

Рисунок 9: набор данных c)

Несмотря на то, что используемые в данном исследовании машины, как и коммуникационная среда, сейчас не используются и считаются устаревшими, результат приведенных экспериментов наглядно показывает, что EM алгоритм хорошо параллелится, зависимость ускорения от числа узлов в кластере с небольшим количеством узлов близка к линейной, а также, что скорость работы алгоритма линейно зависит от числа объектов.

Данный раздел считается незавершенным и может дополняться

2.7 Существующие реализации алгоритма

Примеры библиотек, содержащих последовательную реализацию EM-алгоритма, или отдельных реализаций:

1. OpenCV(C++) (github)
2. Matlab
3. Scikit learn (Python)
4. MLPack(C++)

Примеры библиотек, содержащих параллельную реализацию EM-алгоритма, или отдельных реализаций:

Здесь приводятся как конкретные реализации, так и статьи, описывающие подходы к реализациям распараллеливания EM-алгоритма

1. Apache Spark
2. Accord.NET Framework (C#)
3. статья Parallelizing EM Clustering Algorithm on a Cluster of SMPs
4. реализация с использованием CUDA
5. еще одна реализация с использованием CUDA
6. статья The Parallel EM Algorithm and its Applications in Computer Vision

3 Литература

[9] http://web.cse.ohio-state.edu/~agrawal/allpapers/europar04.pdf

[10] http://www.cs.kent.edu/~jin/Papers/JPDC08.pdf

[11] http://w01fe.com/berkeley/pubs/08-icml-em.pdf

[12] http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.4.8470&rep=rep1&type=pdf

[13] https://arxiv.org/pdf/1606.02054.pdf