Участник:Pandvik/Ортогонализация Грама - Шмидта: различия между версиями
Vvf63 (обсуждение | вклад) |
Pandvik (обсуждение | вклад) (Заполнение раздела "Информационный граф") |
||
| Строка 21: | Строка 21: | ||
== Информационный граф == | == Информационный граф == | ||
| + | Опишем информационный граф алгоритма. | ||
| + | |||
| + | Для вычисления <math>b_i</math> требуется найти <math>proj_{b_{j}}a_{i}</math> для всех <math>j \in [1, i]</math>. Следовательно для полного вычисления вектора <math>b_{i}</math> требуется знать все <math>b_{j}</math> с меньшим индексом. Такая зависимость по данным очень не удачна для параллелизма. Однако, если разбить процесс вычисления <math>b_{i}</math> на несколько этапов, соответствующих функциям проекции (<math>proj_{b_{j}}a_{i}</math>), то это позволит производить некоторые предварительные вычисления для <math>b_{j}</math> до момента, когда станут известны все предшествующие ей <math>b_{i}</math>. | ||
| + | |||
| + | На Рис. 1 изображена зависимость каждого из этапов от предыдущих вычислений. Первая строка овалов содержит все проекции, зависящие от <math>b_{1}</math>, вторая строка - все проекции, зависящие от <math>b_{2}</math>, <math>\;\cdots\;</math> самая верхняя строка содержит проекцию, которая зависит от <math>b_{N-1}</math>. | ||
| + | |||
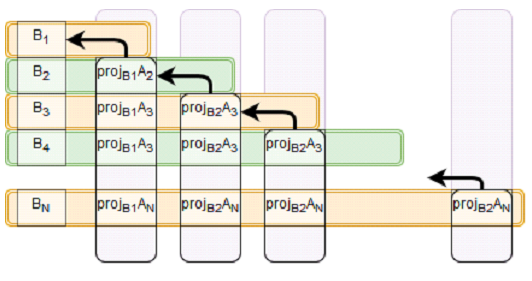
| + | Рис. 2 показывает зависимость по данным немного в другом формате. Каждая строка представляет собой набор данных, которые требуются для вычисления <math>b_{i}</math> из первого столбца. Второй и последующие столбцы группируют проекции, зависящие от одной из <math>b_{i}</math> и, с помощью стрелки, показывают эту зависимость. | ||
| + | |||
| + | [[Файл:Diagram_Gram-Schmidt_DataFlow.png|left|frame|Рис. 1. Информационный граф алгоритма Грама-Шмидта]] | ||
| + | [[Файл:Diagram_Gram-Schmidt_DataFlow_1.png|right|frame|Рис. 2. Информационный граф алгоритма Грама-Шмидта]] | ||
== Ресурс параллелизма алгоритма == | == Ресурс параллелизма алгоритма == | ||
Версия 22:04, 13 октября 2016
Авторы описания алгоритма: Павлов Андрей, Филимонов Владимир.
Содержание
- 1 ЧАСТЬ. Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 ЧАСТЬ. Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 ЧАСТЬ. Свойства и структура алгоритмов
1.1 Общее описание алгоритма
В конечномерном евклидовом пространстве существует ортонормированный базис. Для доказательства этого факта требуется найходить и строить такие базисы. Построить ортонормированный базис можно, отталкиваясь от некоторого исходного базиса, при помощи алгоритма, который называют процессом ортогонализации Грама — Шмидта. Процесс ортогонализации Грама-Шмидта используется для квадратных матриц, которые преобразуются, либо уже преобразованы, к верхнему(нижнему) треугольному виду. Процесс ортогонализации Грама-Шмидта нашёл применение в оптимизации оценивания параметров моделей управления объектом, в протоколах безопасности, в обработке сигналов, в вычислении локальных минимумов целочисленных решёток и многом другом. Обычно, процесс ортогонализации используется как промежуточный шаг в других алгоритмах для уменьшения количества вычислений.
1.2 Математическое описание алгоритма
1.3 Вычислительное ядро алгоритма
1.4 Макроструктура алгоритма
1.5 Схема реализации последовательного алгоритма
1.6 Последовательная сложность алгоритма
1.7 Информационный граф
Опишем информационный граф алгоритма.
Для вычисления [math]b_i[/math] требуется найти [math]proj_{b_{j}}a_{i}[/math] для всех [math]j \in [1, i][/math]. Следовательно для полного вычисления вектора [math]b_{i}[/math] требуется знать все [math]b_{j}[/math] с меньшим индексом. Такая зависимость по данным очень не удачна для параллелизма. Однако, если разбить процесс вычисления [math]b_{i}[/math] на несколько этапов, соответствующих функциям проекции ([math]proj_{b_{j}}a_{i}[/math]), то это позволит производить некоторые предварительные вычисления для [math]b_{j}[/math] до момента, когда станут известны все предшествующие ей [math]b_{i}[/math].
На Рис. 1 изображена зависимость каждого из этапов от предыдущих вычислений. Первая строка овалов содержит все проекции, зависящие от [math]b_{1}[/math], вторая строка - все проекции, зависящие от [math]b_{2}[/math], [math]\;\cdots\;[/math] самая верхняя строка содержит проекцию, которая зависит от [math]b_{N-1}[/math].
Рис. 2 показывает зависимость по данным немного в другом формате. Каждая строка представляет собой набор данных, которые требуются для вычисления [math]b_{i}[/math] из первого столбца. Второй и последующие столбцы группируют проекции, зависящие от одной из [math]b_{i}[/math] и, с помощью стрелки, показывают эту зависимость.