Участник:Бугаков Юрий/Построение матрицы Адамара произвольного размера: различия между версиями
| Строка 189: | Строка 189: | ||
=== Входные и выходные данные алгоритма === | === Входные и выходные данные алгоритма === | ||
| − | '''Входные данные''': | + | '''Входные данные''': размерность матрицы <math>H_n</math> n. |
| − | |||
| − | |||
| − | |||
| − | '''Объём входных данных''': | + | '''Объём входных данных''': 1 (число n). |
| − | '''Выходные данные''': | + | '''Выходные данные''': матрица Адамара <math>H_n</math>. |
| − | '''Объём выходных данных''': | + | '''Объём выходных данных''': . |
=== Свойства алгоритма === | === Свойства алгоритма === | ||
Версия 15:50, 14 октября 2016
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 ЧАСТЬ Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Важную роль в алгебре и комбинаторике играют матрицы Адамара, которые впервые были введены в математический обиход в конце прошлого века одним из крупнейших французских математиков Жаком Адамаром (1865-1963). Их применение в науке и технике посвящены тысячи публикаций. Они предоставляют эффективные возможности для организации хранения, обработки и передачи информации.
Квадратная матрица Н порядка m с элементами ±1 называется матрицей Адамара, если выполняется условие
- H_m\,H_m^T = m\,E_m
Нетрудно заметить, что различные строки матрицы Адамара попарно ортогональны. Также, можно увидеть из определения, что m четно и
- H_{2m} = \begin{pmatrix} H_{m} & H_{m}\\ H_{m} & -H_{m}\end{pmatrix}
С матрицами Адамара связан ряд нерешенных проблем, одна из которых состоит в следующем. Мы уже видели, что порядок m матрицы Адамара при m ≥ 3 может быть лишь четным. Более того, при m ≥ 4 порядок обязан делиться на 4. До сих пор остается открытым вопрос: для любого ли m, кратного 4, существует матрица Адамара порядка m? Неизвестно, в частности, существует ли матрица Адамара порядка 268 (это наименьший порядок, кратный 4, для которого матрица Адамара еще не построена).
Часто матрицу Адамара нормализуют и рассматривают размерности степени 2. В дальнейшем будем рассматривать только такие случаи. Переопределим матрицу Адамара следующим образом:
Матрица Адамара Hn - это матрица размера 2n × 2n, для которой справедливо равенство
- H_n = H_{1} \otimes H_{n-1}
- \begin{align} H_1 = \frac{1}{\sqrt2} &\begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix} \end{align}
где \otimes представляет собой тензорное произведение.
Представим некоторые частные примеры матриц Адамара:
- H_0 = +1,
- H_1 = \frac{1}{\sqrt2} \begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix}
- H_2 = \frac{1}{2} \begin{pmatrix}\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1 \end{array}\end{pmatrix}
- H_3 = \frac{1}{2^{\frac{3}{2}}} \begin{pmatrix}\begin{array}{rrrrrrrr} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1 & 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1 & 1 & -1 & -1 & 1\\ 1 & 1 & 1 & -1 & -1 & -1 & -1 & -1\\ 1 & -1 & 1 & 1 & -1 & 1 & -1 & 1\\ 1 & 1 & -1 & 1 & -1 & -1 & 1 & 1\\ 1 & -1 & -1 & -1 & -1 & 1 & 1 & -1\\ \end{array}\end{pmatrix}
1.2 Математическое описание алгоритма
Основой алгоритма является тот факт, что любую матрицу Адамара H_n, размерностью 2^n\times 2^n можно вычислить поэлементно [ссылочка=)]:
- h_{k,l} = \frac{1}{2^\frac{n}{2}} (-1)^{\sum_j k_j l_j},
где kj и lj коэффициенты двоичного разложения чисел k и l (1 или 0)
- k = \sum^{n}_{i=0} {k_i 2^i} = k_{n} 2^{n} + k_{n-1} 2^{n-1} + \cdots + k_1 2 + k_0
и
- l = \sum^{n}_{i=0} {l_i 2^i} = l_{n} 2^{n} + l_{n-1} 2^{n-1} + \cdots + l_1 2 + l_0.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро составляют вычисления элементов матрицы h_{k,l} = \frac{1}{2^\frac{n}{2}} (-1)^{\sum_j k_j l_j}.
Помимо этой формулы чаще всего используется метод тензорного произведения. В связи с трудностями распараллеливания и постоянного выделения памяти при каждом шаге рекурсивного вызова этого метода, мы решили выбрать первый способ вычисления
1.4 Макроструктура алгоритма
Основную часть метода составляют вычисления значений степени -1 для каждого элемента:
- \sum_{j=0}^n k_j l_j.
Как видно по формуле, получаемое значение равна количеству единиц в двоичной записи результата побитового умножения k и l. Существует эффективный метод вычисления количества единиц , сложность которого равна m операций вычитания и m операций побитового умножения, где m-искомое количество единиц.
1.5 Схема реализации последовательного алгоритма
Последовательность исполнения метода следующая:
1. Побитовое умножение k\&l.
2. Вычисление количества единиц двоичной записи.
3. Определение знака элемента по степени.
1.6 Последовательная сложность алгоритма
Для построения матрицы Адамара порядка 2^n в последовательном варианте требуется:
- 4^n вычислений квад,
- \frac{n(n-1)}{2} делений,
- \frac{n^3-n}{6} сложений (вычитаний),
- \frac{n^3-n}{6} умножений.
Умножения и сложения (вычитания) составляют основную часть алгоритма.
При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности (или использования функции вроде DPROD в Фортране), что ещё больше увеличивает долю умножений и сложений/вычитаний во времени, требуемом для выполнения метода Холецкого.
При классификации по последовательной сложности, таким образом, метод Холецкого относится к алгоритмам с кубической сложностью.
1.7 Информационный граф
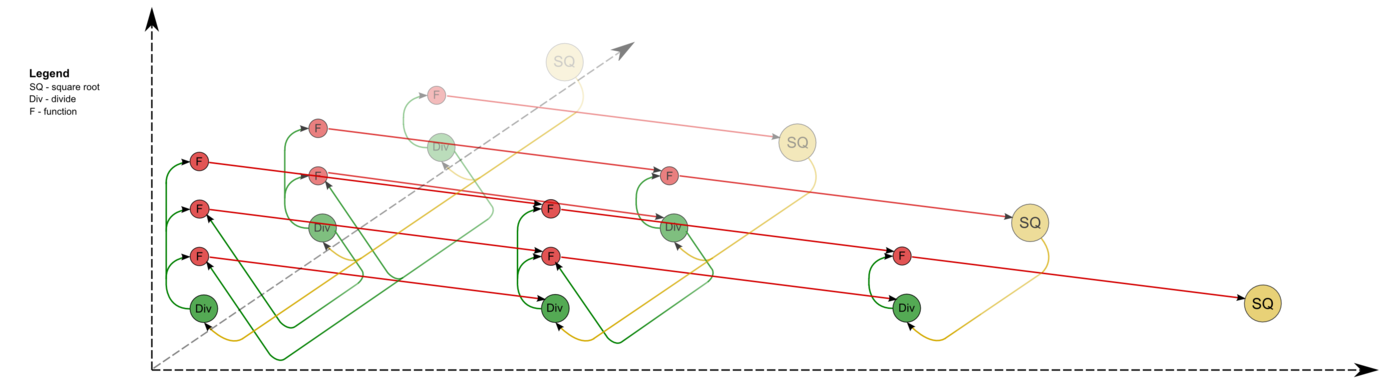
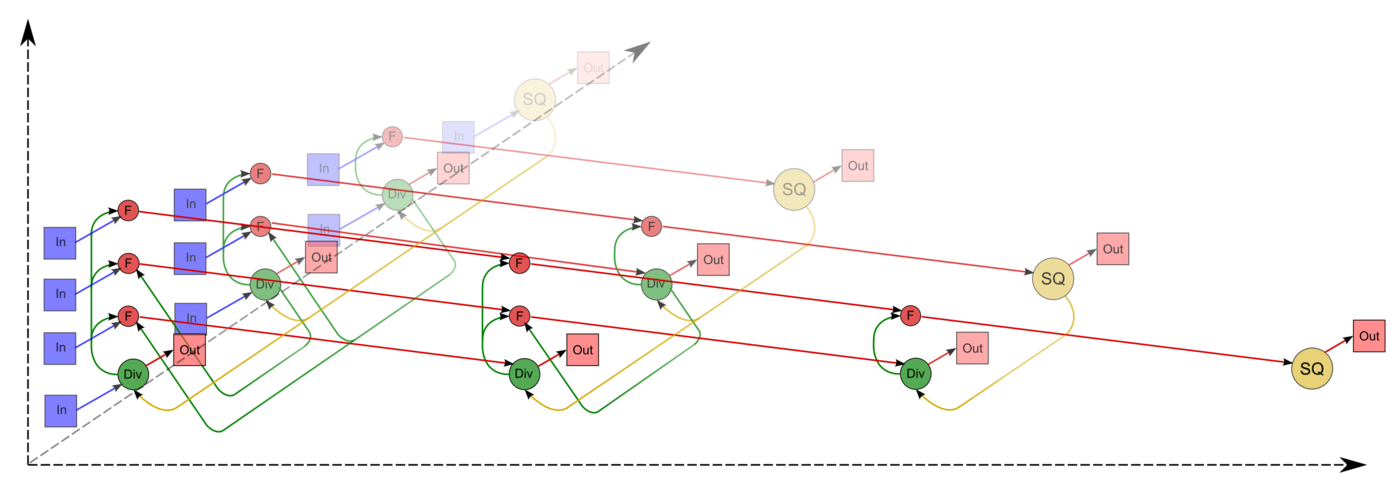
Опишем граф алгоритма[1][2][3] как аналитически, так и в виде рисунка.
Граф алгоритма состоит из трёх групп вершин, расположенных в целочисленных узлах трёх областей разной размерности.
Первая группа вершин расположена в одномерной области, соответствующая ей операция вычисляет функцию SQRT. Единственная координата каждой из вершин i меняется в диапазоне от 1 до n, принимая все целочисленные значения.
Аргумент этой функции
- при i = 1 — элемент входных данных, а именно a_{11};
- при i \gt 1 — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами i - 1, i, i - 1.
Результат срабатывания операции является выходным данным l_{ii}.
Вторая группа вершин расположена в двумерной области, соответствующая ей операция a / b. Естественно введённые координаты области таковы:
- i — меняется в диапазоне от 1 до n-1, принимая все целочисленные значения;
- j — меняется в диапазоне от i+1 до n, принимая все целочисленные значения.
Аргументы операции следующие:
- a:
- при i = 1 — элементы входных данных, а именно a_{j1};
- при i \gt 1 — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами i - 1, j, i - 1;
- b — результат срабатывания операции, соответствующей вершине из первой группы, с координатой i.
Результат срабатывания операции является выходным данным l_{ji}.
Третья группа вершин расположена в трёхмерной области, соответствующая ей операция a - b * c. Естественно введённые координаты области таковы:
- i — меняется в диапазоне от 2 до n, принимая все целочисленные значения;
- j — меняется в диапазоне от i до n, принимая все целочисленные значения;
- p — меняется в диапазоне от 1 до i - 1, принимая все целочисленные значения.
Аргументы операции следующие:
- a:
- при p = 1 элемент входных данных a_{ji};
- при p \gt 1 — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами i, j, p - 1;
- b — результат срабатывания операции, соответствующей вершине из второй группы, с координатами p, i;
- c — результат срабатывания операции, соответствующей вершине из второй группы, с координатами p, j;
Результат срабатывания операции является промежуточным данным алгоритма.
Описанный граф можно посмотреть на рис.1 и рис.2, выполненных для случая n = 4. Здесь вершины первой группы обозначены жёлтым цветом и буквосочетанием sq, вершины второй — зелёным цветом и знаком деления, третьей — красным цветом и буквой f. Вершины, соответствующие операциям, производящим выходные данные алгоритма, выполнены более крупно. Дублирующие друг друга дуги даны как одна. На рис.1 показан граф алгоритма согласно классическому определению , на рис.2 к графу алгоритма добавлены вершины , соответствующие входным (обозначены синим цветом) и выходным (обозначены розовым цветом) данным.
1.8 Ресурс параллелизма алгоритма
Для разложения матрицы порядка n методом Холецкого в параллельном варианте требуется последовательно выполнить следующие ярусы:
- n ярусов с вычислением квадратного корня (единичные вычисления в каждом из ярусов),
- n - 1 ярус делений (в каждом из ярусов линейное количество делений, в зависимости от яруса — от 1 до n - 1),
- по n - 1 ярусов умножений и сложений/вычитаний (в каждом из ярусов — квадратичное количество операций, от 1 до \frac{n^2 - n}{2}.
Таким образом, в параллельном варианте, в отличие от последовательного, вычисления квадратных корней и делений будут определять довольно значительную долю требуемого времени. При реализации на конкретных архитектурах наличие в отдельных ярусах ЯПФ отдельных вычислений квадратных корней может породить и другие проблемы. Например, при реализации на ПЛИСах остальные вычисления (деления и тем более умножения и сложения/вычитания) могут быть конвейеризованы, что даёт экономию и по ресурсам на программируемых платах; вычисления же квадратных корней из-за их изолированности приведут к занятию ресурсов на платах, которые будут простаивать большую часть времени. Таким образом, общая экономия в 2 раза, из-за которой метод Холецкого предпочитают в случае симметричных задач тому же методу Гаусса, в параллельном случае уже имеет место вовсе не по всем ресурсам, и главное - не по требуемому времени.
При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности, а в параллельном варианте это означает, что практически все промежуточные вычисления для выполнения метода Холецкого в режиме накопления должны быть двойной точности. В отличие от последовательного варианта это означает увеличение требуемой памяти почти в 2 раза.
При классификации по высоте ЯПФ, таким образом, метод Холецкого относится к алгоритмам со сложностью O(n). При классификации по ширине ЯПФ его сложность будет O(n^2).
1.9 Входные и выходные данные алгоритма
Входные данные: размерность матрицы H_n n.
Объём входных данных: 1 (число n).
Выходные данные: матрица Адамара H_n.
Объём выходных данных: .
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является квадратичным (отношение кубической к линейной).
При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – всего лишь линейна.
При этом алгоритм почти полностью детерминирован, это гарантируется теоремой о единственности разложения. Использование другого порядка выполнения ассоциативных операций может привести к накоплению ошибок округления, однако это влияние в используемых вариантах алгоритма не так велико, как, скажем, отказ от использования режима накопления.
Дуги информационного графа, исходящие из вершин, соответствующих операциям квадратного корня и деления, образуют пучки т. н. рассылок линейной мощности (то есть степень исхода этих вершин и мощность работы с этими данными — линейная функция от порядка матрицы и координат этих вершин). При этом естественно наличие в этих пучках «длинных» дуг. Остальные дуги локальны.
Наиболее известной является компактная укладка графа — его проекция на треугольник матрицы, который перевычисляется укладываемыми операциями. При этом «длинные» дуги можно убрать, заменив более дальнюю пересылку комбинацией нескольких ближних (к соседям).
Эквивалентное возмущение M у метода Холецкого всего вдвое больше, чем возмущение \delta A, вносимое в матрицу при вводе чисел в компьютер: ||M||_{E} \leq 2||\delta A||_{E}
Это явление обусловлено положительной определённостью матрицы. Среди всех используемых разложений матриц это наименьшее из эквивалентных возмущений.
2 ЧАСТЬ Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
3 Литература
- ↑ Воеводин В.В. Математические основы параллельных вычислений// М.: Изд. Моск. ун-та, 1991. 345 с.
- ↑ Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ - Петербург, 2002. – 608 с.
- ↑ Фролов А.В.. Принципы построения и описание языка Сигма. Препринт ОВМ АН N 236. М.: ОВМ АН СССР, 1989.