Участник:Bagnikita/Face Recognition

Распознавание лиц
Последовательный алгоритм
Последовательная сложность	[math]O(E(w,h,c)+n*d+n*logn+n*logk+CNNConst)[/math]
Объём входных данных	[math]w*h*c[/math]
Объём выходных данных	[math]O(k)[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(k)[/math]
Ширина ярусно-параллельной формы	[math]O(n)[/math]

Основные авторы описания: Н.Ю.Багров

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Распознавание лиц при помощи компьютера было впервые предложено в 1966 г. Woody Bledsoe и др. В первой системе использовался графический планшет, на котором было необходимо вручную отметить ключевые особенности на лице (брови, губы и тд). Система в дальнешейм использовала расстояния между этими точками для сравнения разных изображений. Поскольку требовалось много ручной работы, то оператор мог обработать около 40 изображений в час. В 1997 была создана система, которая непосредственно работала с видеоданными и могла применяться на практике. В дальшейшем с увеличением производительности вычислительных систем появились более качественные алгоритмы, но они заметно уступали человеку на данной задаче. С появлением высокороизводительных видеокарт в 2014 году появились системы, точность которых уже превышала точность оператора (человека). Основное преимущество таких систем в том, что они могут обрабатывать большие объемы данных - производительность человека намного ниже (требуется несколько секунд на сравнение пары изображений).

Задачу распознавания лиц можно разбить на несколько этапов:

• обучение нейронной сети
• построение биометрического шаблона
• сравнение биометрических шаблонов
• поиск в базе и формирование результата

1.2 Математическое описание алгоритма

Алгоритм состоит из построения биометрических шаблонов (дескрипторов) по изображению и поиску заданного шаблона в базе уже вычисленных дескрипторов.

В дальшейшем будем рассматривать только сверточные нейронные сети. Классические архитектуры нейронных сетей с полносвязными слоями неприменимы на практике для анализа изображений, поскольку количество параметров такой сети экспоненциально возрастает с размером входных данных и количеством слоев. В таких сетях каждый нейрон не связан со всеми нейронами предыдущего слоя, а домножается на некоторый коэффициент (ядро свертки) по всему изображению. Таким образом, каждый такой слой применяет операцию свертки ко входам со своими коэффициентами, что заметно уменьшает число весов в нейронной сети. Это позволяет уменьшить потребление памяти и эффект переобучения сети, который проявляется в том, что сеть хорошо работает на классификации элементов обучающей выборки и хуже на валидационной.

1.2.1 Обучение сверточной нейронной сети

Для обучения нейронной сети используется стохастический градиентный спуск. Начальные веса сети устанавливаются случайными. Заметим, что существенное время занимают сверточные и полносвязные слои. Их можно свести к операции перемножения матриц следуюим образом:

• пусть размерность фильтра свертки k*k
• скопируем блоки исходного изображения размером k*k в столбцы новой матрицы
• умножим эту матрицу на коэффициеты фильтра свертки
• полученная матрица будет результатом применения свертки к входному изображению

Сложность задачи вычисления свертки зависит квадратично от размера фильтра и линейно от количества выходных данных.

[math]FeatureMap = A^{n, w * h} * B^{w * h, c * k^2}[/math], где [math]FeatureMap[/math] - результат применения свертки, а [math]A[/math] и [math]B[/math] - входное изображение и матрица весов слоя нейронной сети

Существуют библиотеки (NVIDIA cuDNN) которые решают данную задачу более эффективно. Например, свертки размером 3x3, 5x5 могут быть реализованы с использованием FFT (что работает на видеокарте быстрее, чем умножение матриц)

1.2.2 Построение биометрического шаблона

Будем называть биометрическим шаблоном вектор [math]{R}^d[/math], который является представлением лица человека. Этот вектор получается после применения нейронной сети к изображению - в качестве такого вектора используют отклики с одного последних слоев нейронной сети. Для обеспечения возможности сравнивать между собой эти шаблоны вектор нормализуют.

1.2.3 Сравнение биометрических шаблонов

На предыдущем этапе был получен вектор значений [math]D={A}^d[/math], где d - размерность дескриптора. Можно рассматривать достаточно много различных оценивающих функций (метриками их называть некорректно, т.к для них не всегда выполняется неравенство треугольника). Например, в качестве такой функции можно рассматривать cosine distance - косинус угла между векторами-признаками в d-мерном пространстве. Также достаточно часто используют L2 метрику, либо более сложные контрукции, такие как Joint Bayesian. У всех таких "метрик" есть преимущества и недостатки, например в L2 можно легко проводить кластеризацию, тогда как в JointBayes и cosine metric нет. JointBayes можно дообучить на целевой выборке и повысить точность работы алгоритма.

1.2.4 Поиск в базе и формирование результата

Предположим, что для каждого человека в базе есть несколько фотографий. Тогда после выполнения операции сравнения биометрических шаблона изображения-запроса [math]P[/math] и всех изображений в базе [math]G={g1,g2,...,gn}[/math] необходимо выбрать результат с максимальным значением оценивающей функции для данного человека. Т.е необходимо оставить в результате только уникальные по людям совпадения, выбрав при этом максимальное значение при удалении дубликатов по людям.

После выполнения поиска в базе необходимо произвести нормализацию полученных значений оценивающей функции. В системах распознавания лиц обычно используют диапазон [0.0 - 1.0], где 0.0 означает минимальное сходство двух изображений лиц, а 1.0 максимальное.

1.3 Вычислительное ядро алгоритма

Основные операции составляют построение биометрического шаблона, и поиск в базе

1.3.1 Построение биометрического шаблона

Обозначим за [math]E(w,h,c)[/math] сложность операции вычисления биометричсекого шаблона по входному изображению лица человека. Поскольку сверточной нейронной сети с полносвязными слоями должно подаваться на вход изображения фиксированного размера, то необходимо изменить разрешение исходного изображения. В данной реализации алгоритма распознавания лиц используется билинейная интерполяция. Нейронная сеть получает на вход одноканальные изображения размером [math]100*100[/math]. Поэтому число необходимых операций (по операциям умножения) можно оценить как [math]O(w*h*c) + O(100 * 100 * 6) = O(w*h*c) + Const[/math]. На практике эта константа существенна, поскольку эти операции неоднородны по памяти.

Непосредственно время работы нейронной сети существенно зависит от предложенной архитектуры (глубины сети, типов слоев и числа выходов каждого слоя).

В реализации, предлолженной в практической части, используются более 10 сверточных слоев. Количестве операций можно оценить исходя из количества весов связей в нейронной сети - 80M и размера сверток [math]3*3[/math]. Оценка числа операций получилась ~2 GFlops на одну операцию применения нейросети (forward pass, 180ms). Она согласуется с реальным временем работы системы и производительностью системы на тесте linpack (130GFlops 4 cores) на ноутбуке.

1.3.2 Поиск в базе

Поиск в базе состоит из следующих частей:

• сравнение между собой двух дескрипторов изображений и вычисление метрики по базе
• агрегация результатов по людям
• сортировка по убыванию метрики сходства двух изображений

1.3.2.1 Сравнение между собой двух дескрипторов изображений и вычисление метрики по базе

В практической реализации алгоритма используется косинусовая метрика [math]M(x,y)=\frac{(x,y)}{\lVert x \lVert * \lVert y \lVert}[/math]. Заметим, что вектора [math]x, y[/math] уже нормированы на предыдущем этапе. Поэтому число операций для вычисления метрики составляет [math]d[/math] умножений и [math]d - 1[/math] сложений, где d - размерность дескриптора. Если размер базы [math]n[/math], то число операций [math]O(n*d+n*(d-1))=O(n*d)[/math].

1.3.2.2 Агрегация результатов по людям

Для выполнения операции unique (без использования дополнительной памяти) необходимо отсортировать элементы (person_id, match_score) массива по ключу person_id, а при совпадении по score. После этого можно за линейное время удалить дубликаты по person_id, оставив первый элемент (который будет максимальным по match_score). Сложность таких операций [math]O(n*logn+n)=O(n*logn)[/math].

1.3.2.3 Cортировка по убыванию метрики сходства двух изображений

Финальная сортировка по match_score будет выполнена за O(n*logk), где k - количество результатов в выдаче. Обычно на практике число k не более 1000, поскольку обработка результата чаще всего производится вручную оператором.

1.4 Макроструктура алгоритма

Алгоритм содержит вычисление биометричиского шаблона, который на этой странице не приводится. Используется готовая бибилотека распознавания лиц Tevian FaceSDK. Предложенная параллельная реализация может работать с любой системой распознавания лиц, для которой выполнены следующие условия:

• известна метрика для сравнения
• можно получить дескрипторы (биометрические шаблоны) в явном виде

1.5 Схема реализации последовательного алгоритма

Алгоритм можно представить в виде следующего фрагмента псевдокода (он менее эффективный, чем предложенный выше. Эффективная реализация на c++):

desc = enroll(Image) # Image - изображение лица человека
matches = {}
for gallery_entry in G:
    if matches.get(gallery_entry.person_id, None) is None:
        matches[gallery_entry.person_id] = 0.0
    matches[gallery_entry.person_id] = max(matches[gallery_entry.person_id], match(desc, gallery_entry.descriptor))
matches = sorted(key = lambda x: x[1], matches.items())
return [x[0], applyMapping(x[1]) for x in matches]

1.6 Последовательная сложность алгоритма

Если рассматривать всю последовательность действий (построение шаблона, поиск в базе), то сложность алгоритма [math]O(E(w,h,c)+n*d+n*logn+n*logk+CNNConst)[/math], где

• [math]n[/math] - число элементов в базе
• [math]d[/math] - размерность биометрического шаблона
• [math]E(w,h,c)[/math] - сложность обработки изображения размером (width*height*channels) до необходимого размера для нейросети
• [math]n*d[/math] - число операций для вычисления метрики между запросом и базой
• [math]n*logn[/math] - сортировка результата для удаления дубликатов
• [math]n*logk[/math] - сортировка результата по значению оценивающей функции

1.7 Информационный граф

TODO

1.8 Ресурс параллелизма алгоритма

Сложность параллельного алгоритма, в предположении доступности q узлов: [math]O(k*logk+q*(log(k*q))^2+\frac{n}{q}*(d+log(\frac{n}{q}))+\lambda*(k*log(q)+q*(log(q*k))^2))[/math], где

• n - размер базы изображений лиц
• d - размерность биометрического шаблона
• k - количество результатов в выдаче (k << n)
• [math]\lambda[/math] - флаг (0 или 1), нужно ли производить агрегацию результатов по людям

Данная оценка получена с применением параллельной сортировки.

1.9 Входные и выходные данные алгоритма

Входные данные:

• изображение [math]P\in{R}^{w*h*c}[/math], где w,h,c - ширина, высота, число каналов
• база изображений лиц [math]G={g_1,g_2,g_3,...,g_n}, g_i\in{T}[/math]
• T - объект, состоящий из биометрического шаблона и порядкового номера человека

Выходные данные*

• список [math]L={l_1,l_2,...,l_k}[/math], где [math]l_i\in{T}[/math]
• T - объект, состоящий из числа (мера сходства двух изображений) и id (порядкового номера) человека в базе

1.10 Свойства алгоритма

Основная проблема при реализации параллельной версии данного алгоритма - необходимость сортировки результатов. Исходя из размеров базы важно правильно выбрать количество вычислителей, поскольку в ряде случаев сортировка будет работать очень быстро (число элементов будет значительно меньше объема базы) и не потребуется реализация параллельной сортировки.

Другая проблема - низкая вычислительная сложность самого алгоритма и большое число обращений к памяти. При реализации важно выделять память большими блоками для успешного чтения из кэша процессора.

Из преимуществ данного алгоритма можно назвать низкую нагрузку на сеть при обмене данными, возможность работы на множестве систем (MPI, hadoop и тд), посколько объем данных, передаваемых между узлами небольшой. Для практической реализации не требуется использования специальных коммуникаций с низкой задержкой (обмены происходят достаточно редко, время доставки сообщений не критично).

2 Практическая реализация системы

Построение биометрических шаблонов выполнено при помощи библиотеки распознавания лиц FaceSDK. В этом разделе приводится эффективность параллельной реализации сравнения изображени лица с некоторой базой лиц.

2.1 Быстрое сравнение биометрических шаблонов

При выполнении оценки производительности системы использовалась простая реализация cosine метрики (цикл для вычисления скалярного произведения) и с использованием FMA инстукций. Набор инструкций FMA позволяет выполнять операцию [math]y = ax + b[/math] без дополнительных операций.

Псевдокод операции mm256_fmadd (intel)

FOR j := 0 to 7
    i := j*32
    dst[i+31:i] := (a[i+31:i] * b[i+31:i]) + c[i+31:i]
ENDFOR
dst[MAX:256] := 0

В результате тестирования (процессор 6300HQ, ноутбук, база 30М биометрических шаблонов) однопоточной программы было установлено, что FMA3 версия в 5 раз быстрее по сравнению с обычным циклом (880ms vs 4600ms). Все дальнейшие экспериенты будут проводиться с FMA3 реализацией (если не указано иначе). Компиляция производится gcc 5.4 с флагами -O3 -static-libgcc -static-libstdc++ -mavx -mavx2 -mfma -fopenmp

Применение openmp позволило ускорить версию с обычным циклом до 1300ms, что медленнее FMA3. Вычисление в несколько потоков не ускорило реализацию на FMA3. Вероятно, причина в пропускной способности оперативной памяти - для DDR4 15GBps на канал. Объем тестовой базы 15.5GB, поэтому не менее 500ms должно было занять чтение из памяти.

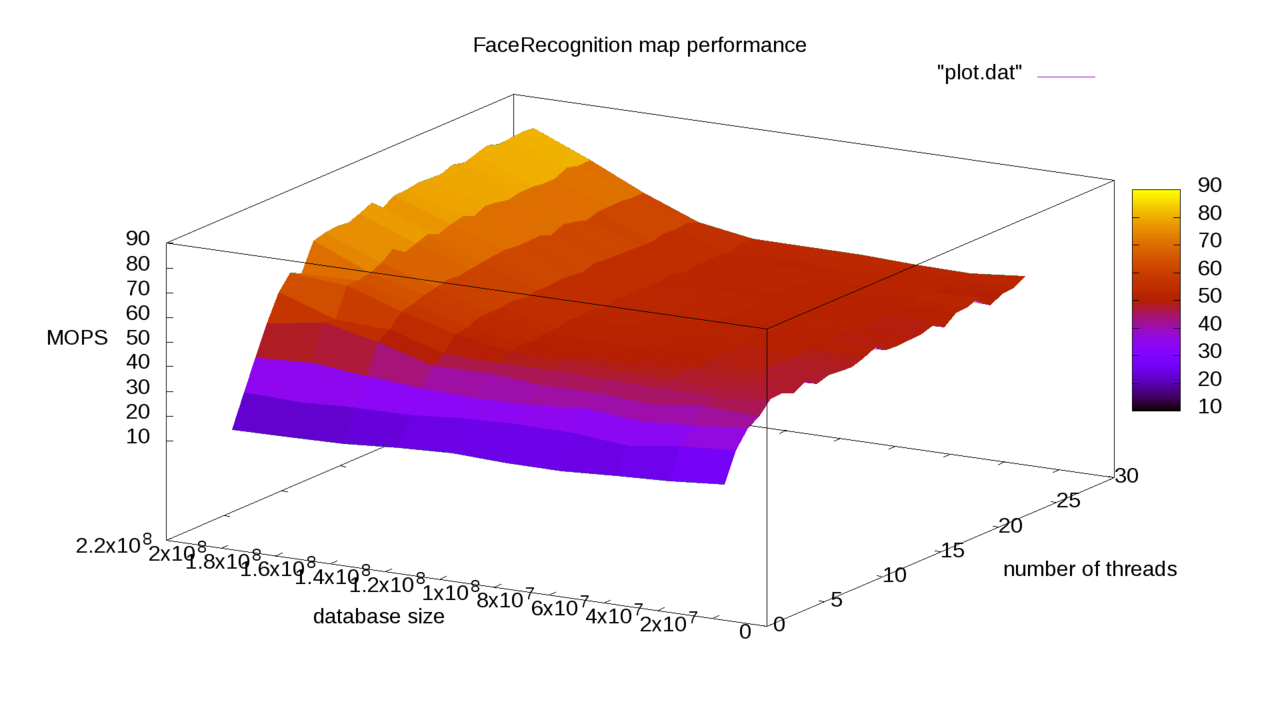
На сервере (2x E5-2683v3 256GB RAM, база 150М биометрических шаблонов) получилось следующее ускорение от использования FMA3 + OpenMP (MOPS - количество операций сравнения в секунду):

Также в процессе тестирования было замечено, что при превышении размера базы лиц объема оперативной памяти, напрямую доступной одному из процессоров, скороость работы снижается.

Количество операций с плавающей точкой (умножения) для сравнения биометрических шаблонов: [math]n*128[/math] FLOP.

2.2 Быстрое формирование результата

Если на каждой операции поиска изображения в базе необходимо выбирать максимальную фотографию для каждого челокека в базе, то задача сводится к классической map/reduce:

• map - вычисление скалярных произведений
• reduce - группировка результатов по людям и выдача N максимально похожих

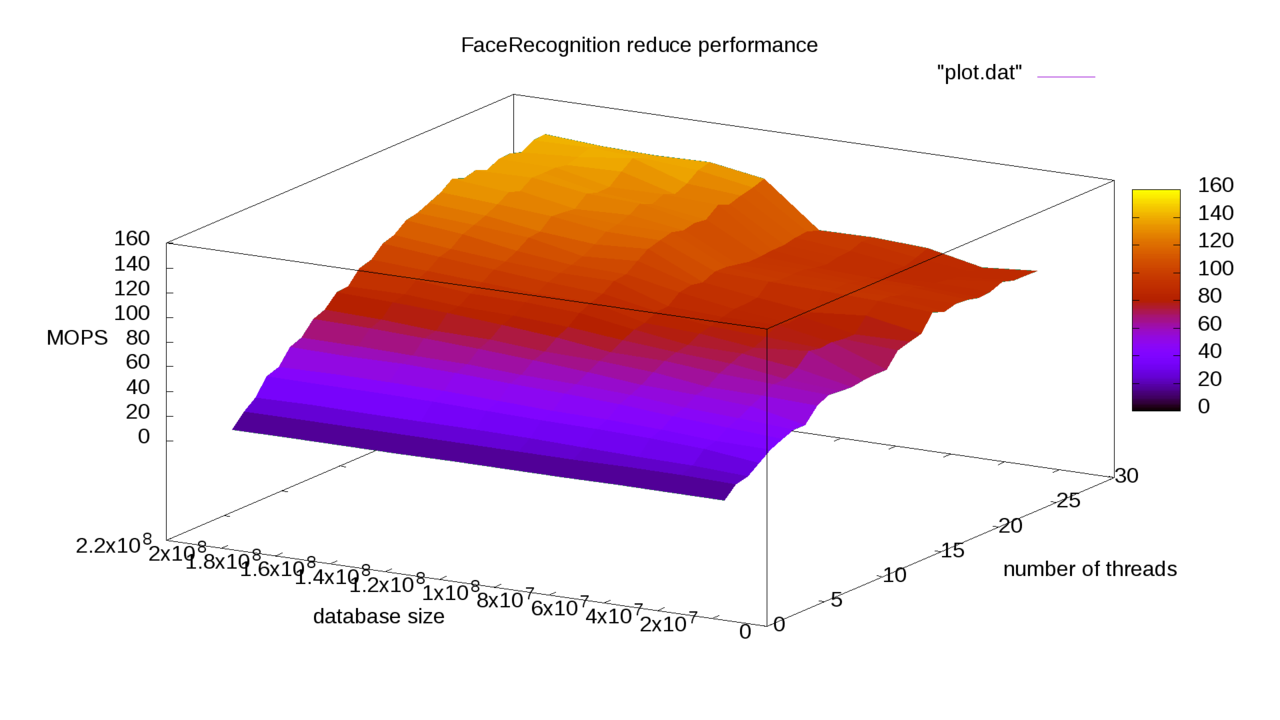
В reduce применение openmp позволило увеличить скорость с 3000ms до 1000ms на 4 ядрах процессора (ноутбук с 6300HQ, 30M записей в базе)

Из дальшейнего фрагмента кода очевидно, что при таком распараллеливании нет зависимостей по переменным. Эксперимент показал, что применять openmp для inplace_merge неэффективно для текущих ограничений на размер базы (200-300M).

vector<MatchResult> OMP_Blob::reduce(size_t top_k, bool merge_person)
{
    const int num_chunks = static_cast<int>(_chunks.size());

    vector<MatchResult> result;
    vector<vector<MatchResult>> results(num_chunks);
    #pragma omp parallel for num_threads(_num_threads)
    for(int i = 0; i < num_chunks; ++i) {
        results[i] = _chunks[i].reduce(top_k, merge_person, false);
    }

    for(int i = 0; i < num_chunks; ++i) {
        result.insert(result.end(), results[i].begin(), results[i].end());
    }

    if(merge_person) {
        size_t csum = 0;
        for(int i = 0; i < num_chunks; ++i) {
            inplace_merge(result.begin(), result.begin() + csum, result.begin() + csum + results[i].size(), [](const MatchResult &a, const MatchResult &b) {
                return a.person_id < b.person_id || (a.person_id == b.person_id && a.score > b.score);
            });
            csum += results[i].size();
        }
        result.resize(unique(result.begin(), result.end(), [](const MatchResult &a, const MatchResult &b) {
            return a.person_id == b.person_id;
        }) - result.begin());
    }
    size_t result_size = min(top_k, result.size());
    partial_sort(result.begin(), result.begin() + result_size, result.end(), [](const MatchResult &a, const MatchResult &b) {
        return a.score > b.score;
    });
    result.resize(result_size);
    result.shrink_to_fit();
    return result;
}

Финальную сортировку результатов по score ускорять не требуется, поскольку top_k на практике не более 1000. Параллельная реализация в данном случае будет неэффективна.