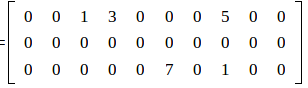Участник:Lexaloris/Умножение разреженной матрицы на вектор: различия между версиями
Lexaloris (обсуждение | вклад) |
Lexaloris (обсуждение | вклад) |
||
| Строка 19: | Строка 19: | ||
Одной из наиболее широко используемых схем хранения разреженных матриц является разреженный строчный формат. Эта | Одной из наиболее широко используемых схем хранения разреженных матриц является разреженный строчный формат. Эта | ||
схема предъявляет минимальные требования к памяти и в то же время оказывается очень удобной для умножения разреженной матрицы на вектор. | схема предъявляет минимальные требования к памяти и в то же время оказывается очень удобной для умножения разреженной матрицы на вектор. | ||
| − | + | Например, рассмотрим формат хранения разряженной матрицы <math>A</math>: | |
| − | [[ | + | [[File:RRCOMatrix.png]] |
| + | Значения ненулевых элементов матрицы и соответствующие столбцовые индексы хранятся в этой схеме по строкам в двух массивах; назовем их соответственно <math>AN</math> и <math>JA</math>. Используется также массив указателей <math>IA</math>, отмечающих позиции массивов <math>AN</math> и <math>JA</math>, с которых начинается описание очередной строки. Дополнительная компонента в <math>IA</math> содержит указатель первой свободной позиции в <math>JA</math> и <math>AN</math>. | ||
| + | |||
| + | Таким образом <math>A</math> представляется в виде: | ||
| + | |||
| + | IA = 1 4 4 6 | ||
| + | JA = 3 4 8 6 8 | ||
| + | AN = 1 3 5 7 1 | ||
| + | |||
| + | Данный способ представления называют полным, поскольку представлена вся матрица А, и упорядоченным, поскольку элементы каждой строки хранятся в соответствии с возрастанием столбцовых индексов. Таким образом, это строчное представление, полное и упорядоченное, или сокращенно RR (С) О. | ||
Пусть <math>N</math> — число строк матрицы. | Пусть <math>N</math> — число строк матрицы. | ||
Версия 16:19, 15 октября 2016
| Умножение разреженной матрицы на вектор | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(k)[/math] |
| Объём входных данных | [math]k + m[/math] |
| Объём выходных данных | [math]n[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(m)[/math] |
| Ширина ярусно-параллельной формы | [math]O(n)[/math] |
Авторы страницы: A.Д. Новоселов и П.А. Кочетков
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
1.1.1 Хранение ненулевых элементов разреженной матрицы
Одной из наиболее широко используемых схем хранения разреженных матриц является разреженный строчный формат. Эта схема предъявляет минимальные требования к памяти и в то же время оказывается очень удобной для умножения разреженной матрицы на вектор. Например, рассмотрим формат хранения разряженной матрицы [math]A[/math]:
Значения ненулевых элементов матрицы и соответствующие столбцовые индексы хранятся в этой схеме по строкам в двух массивах; назовем их соответственно [math]AN[/math] и [math]JA[/math]. Используется также массив указателей [math]IA[/math], отмечающих позиции массивов [math]AN[/math] и [math]JA[/math], с которых начинается описание очередной строки. Дополнительная компонента в [math]IA[/math] содержит указатель первой свободной позиции в [math]JA[/math] и [math]AN[/math].
Таким образом [math]A[/math] представляется в виде:
IA = 1 4 4 6 JA = 3 4 8 6 8 AN = 1 3 5 7 1
Данный способ представления называют полным, поскольку представлена вся матрица А, и упорядоченным, поскольку элементы каждой строки хранятся в соответствии с возрастанием столбцовых индексов. Таким образом, это строчное представление, полное и упорядоченное, или сокращенно RR (С) О.
Пусть [math]N[/math] — число строк матрицы. Для каждой ее строки [math]I[/math] матрийы мы находим с помощью [math]IA[/math] значения первой [math]IAA[/math] и последней [math]IAB[/math] позиций, занимаемых элементами строки [math]I[/math] в массивах [math]JA[/math] и [math]AN[/math]. Затем, чтобы вычислить скалярное произведение строки [math]I[/math] и вектора [math]B[/math], мы просто просматриваем [math]JA[/math] и [math]AN[/math] на отрезке от [math]IAA[/math] до [math]IAB[/math]: каждое значение, хранимое в [math]JA[/math], есть столбцовый индекс и используется для извлечения из массива [math]B[/math] элемента, который должен быть умножен на соответствующее число из [math]AN[/math]. Результат каждого умножения прибавляется к [math]C(I)[/math].
1.2 Математическое описание алгоритма
Исходные данные:
[math]IA, JA, AN[/math] - заданная матрица в форме RR (С) U;
[math]B[/math] - заданный заполненный вектор;
[math]N[/math] - число строк матрицы.
Выход: [math]C[/math] вектор-произведение размерности [math]N[/math].
Формулы метода:
- [math] \begin{align} & IAA_{i} = IA(i), \quad i \in [1, N], \\ & IAB_{i} = IA(i + 1) - 1, \quad i \in [1, N], \\ & c_{i} = \sum\limits_{j = IAA_{i}}^{IAB_{i}} AN(j)B(JA(j)), \quad i \in [1, N] \\ \end{align} [/math]
1.3 Вычислительное ядро алгоритма
Вычислительным ядром, т.е. той частью алгоритма, на которую приходится основное время его работы, является вычисление значения [math]i[/math]-го элемента [math]c_{i}[/math] вектора-произведения, т.е произведения строки [math]I[/math] матрицы [math]A[/math] и вектора [math]B[/math] по формуле:
- [math] \begin{align} & c_{i} = \sum\limits_{j = IAA_{i}}^{IAB_{i}} AN(j)B(JA(j)), \quad i \in [1, N] \\ \end{align} [/math]
1.4 Макроструктура алгоритма
1.5 Схема реализации последовательного алгоритма
Последовательность исполнения метода следующая:
Далее для всех [math]i[/math] от [math]1[/math] до [math]N[/math] по нарастанию выполняются:
1. [math] c_{i} = 0; IAA = IA(i); IAB = IA(i + 1 ) - 1 [/math]
После этого, если [math](IAB \lt = IAA)[/math]:
2. Для всех [math]j[/math] от [math]IAA[/math] до [math]IAB[/math] выполняется:
[math]c_{i} = \sum\limits_{j = IAA_{i}}^{IAB_{i}} AN(j)B(JA(j))[/math]
1.6 Последовательная сложность алгоритма
Для всего алгоритма потребуется выполнить [math]O(M)[/math] операций, где [math]M[/math] - число ненулевых элементов матрицы.
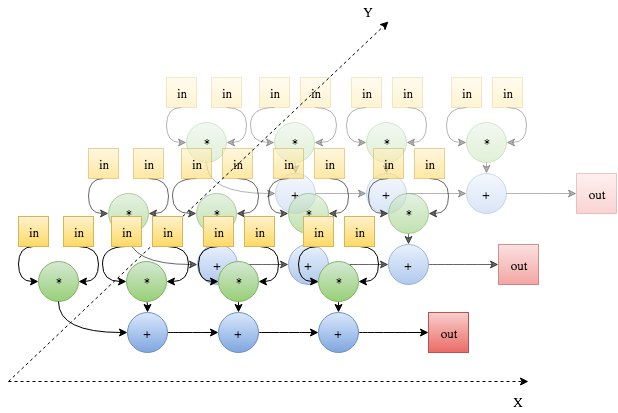
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
1.9 Входные и выходные данные алгоритма
1.10 Свойства алгоритма
Алгоритм в рамках выбранной версии полностью детерминирован.
Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – константа.
2 Программная реализация алгоритма
2.1 Масштабируемость алгоритма и его реализации
2.2 Существующие реализации алгоритма
3 Литература
[1] С. Писсанецки. Технология разреженных матриц. Изд. Мир, 1988.