Участник:KibAndrey/Ортогонализация Грама-Шмидта

Ортогонализация Грама-Шмидта
Последовательный алгоритм
Последовательная сложность	[math]O\left(n^2k\right)[/math]
Объём входных данных	[math]kn[/math]
Объём выходных данных	[math]kn[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(k\log{n})[/math]
Ширина ярусно-параллельной формы	[math]O(kn)[/math]

Основные авторы описания: А.В.Кибанов, Т.З.Аджиева.

1 ЧАСТЬ. Свойства и структура алгоритма

1.1 Общее описание алгоритма

Процесс ортогонализации Грама–Шмидта — алгоритм построения для данной линейно независимой системы векторов евклидова или эрмитова пространства [math]V[/math] ортогональной системы ненулевых векторов, которые имеют ту же самую линейную оболочку, при котором каждый вектор построенной системы линейно выражается через векторы данной системы. Исторически это первый алгоритм, описывающий процесс ортогониализации. Традиционно его связывают с именами Йоргена Педерсена Грама и Эрхарда Шмидта. Йорган Педерсен Грам был датским актуарием, который в неявном виде представил суть процесса ортогонализации в 1883 году. Ясно, что Грам не знал о том, что Лаплас ранее использовал этот метод. Эрхард Шмидт был учеником великих математиков Германа Шварца и Давида Гильберта. Алгоритм ортогонализации был опубликован Э. Шмидтом в 1907 году в его исследовании интегральных уравнений, которое в свою очередь дало привело к развитию теории гильбертовых пространств. Шмидт использовал процесс ортогонализации применительно к геометрии гильбертова пространства решений интегральных уравнений отмечал, что процесс ортогонализации принципиально такой же, какой прежде использовал Й. Грам. В отечественной литературе иногда этот процесс называют "ортогонализацией Сонина–Шмидта". Это название связано с тем, что разработанный Сониным метод ортогонализации системы функций для частного случая по существу не отличается от метода ортогонализации системы функций, предложенного ранее Шмидтом.

1.2 Математическое описание алгоритма

Bходные данные: [math]k[/math] линейно независимых векторов [math]\mathbf{a_1},\mathbf{a_2},\ldots,\mathbf{a_k}[/math] длины [math]n[/math] [math]\left(\alpha_{ij}\right.[/math], [math]j=1,2, \ldots,n[/math], — координаты вектора [math]\left.\mathbf{a_i}\right)[/math] .

Вычисляемые данные:

[math]k[/math] ортогональных векторов [math]\mathbf{b_1},\mathbf{b_2},...,\mathbf{b_k}[/math] длины [math]n[/math], причем [math]\mathbf{b_1}=\mathbf{a_1}[/math], либо

[math]k[/math] ортонормированных векторов [math]\mathbf{q_1},\mathbf{q_2},\ldots,\mathbf{q_k}[/math] длины [math]n[/math], причем [math]\mathbf{q_i}=\frac{\mathbf{a_i}}{|\mathbf{a_i}|}[/math], [math]i=1,2, \ldots,k[/math]. Формулы процесса ортогонализации:

[math] \begin{align} \mathbf{b_{1}} & =\mathbf{a_{1}}, \\ \mathbf{b_{2}}& =\mathbf{a_{2}}-proj_{\mathbf{b_1}}\mathbf{a_{1}}, \\ & ...\\ \mathbf{b_{{i} }} & = \mathbf{a_{i}}-\sum\limits_{j=1}^{i-1} proj_{\mathbf{b_j}}\mathbf{a_{i}},\\ & ...\\ \mathbf{b_{k}} & =\mathbf{ a_{k}}-\sum\limits_{j=1}^{k-1} proj_{\mathbf{b_j}}\mathbf{a_{k}}.\\ \end{align} [/math]

Здесь [math]proj_{\mathbf{b_j}}\mathbf{a_{i}}[/math], для [math]j=1,...,i-1[/math] — проекция вектора [math]\mathbf{a_{i}}[/math] на направление вектора [math]\mathbf{b_{j}}[/math]. Это число, равное по величине проекции вектора [math]\mathbf{a_{j}}[/math] на ось, проходящую через вектор [math]\mathbf{b_j}[/math].

Формула для ее вычисления, полученная из определения скалярного произведения: [math]proj_{\mathbf{b_j}}\mathbf{a_{i}}=\dfrac{(ai,bj)}{\mathbf{\left \|b_j\right \|}}[/math], для [math]j=1,...,i-1[/math]

В этом случае знаменатель в формуле для вычисления проекции [math]|\mathbf{e_i}|=1[/math] для [math]i=1,...,k-1[/math], что существенно упрощает вычисления алгоритма.

Произведение длин [math]\mathbf{|b_1|},\mathbf{|b_2|},\ldots ,\mathbf{|b_k|}[/math] равно объему параллелепипеда, построенного на векторах системы [math]\left\{\mathbf{a_i}\right\}[/math], [math]i=1,2,\ldots ,k[/math], как на ребрах.

Явное выражение векторов [math]\mathbf{b_i}[/math] для [math]i=1,...,k[/math] через [math]\mathbf{a_1},\mathbf{a_2},...,\mathbf{a_k}[/math] дает формула

[math] \mathbf{b_i}= \begin{vmatrix} (a_1,a_1) & \cdots & (a_1,a_k-1) &a_1 \\ \cdots & \cdots & \cdots & \cdots \\ (a_{i},a_1) & \cdots & (a_i,a_k-1) &a_i \\ \cdots & \cdots & \cdots& \cdots \\ (a_{k},a_1) & \cdots & (a_k,a_k-1) &a_k \end{vmatrix} [/math]. (В правой части этого равенства определитель следует формально разложить по последнему столбцу).

Иногда полученные векторы нормируются сразу после их нахождения и находится система ортонормированных векторов [math]\mathbf{q_1},\mathbf{q_2},\ldots,\mathbf{q_k}[/math]. В этом случае знаменатель в формуле для вычисления проекции [math]|\mathbf{e_i}|=1[/math] для [math]i=1,...,k-1[/math], что существенно упрощает вычисления алгоритма. В настоящей статье примененяя процесс ортогонализации к системе линейно независимых векторов, мы так и будем поступать.

1.3 Макроструктура алгоритма

Как записано и в описании ядра алгоритма, основную часть метода составляют вычисления скалярных произведений, как при вычислении длины очередного вектора так и для расчета проекций прочих векторов на новый базисный, а также умножение вектора на число, используемое при корректировке значений остальных векторов после вычисления очередного базисного вектора.

1.4 Схема реализации последовательного алгоритма

Входные данные: [math]k[/math] линейно независимых векторов [math]\mathbf{a_1},\mathbf{a_2},\ldots,\mathbf{a_k}[/math] длины [math]n[/math] [math]\left(\alpha_{ij}\right.[/math], где [math]j=1,2, \ldots,n[/math] — координаты вектора [math]\mathbf{a_i}[/math], для [math]\left.i=1,2, \ldots,k\right)[/math].

Вычисляемые данные:

[math]k[/math] ортогональных векторов [math]\mathbf{b_1},\mathbf{b_2},...,\mathbf{b_k}[/math] длины [math]n[/math] [math]\left(\beta_{ij}\right.[/math], где [math]j=1,2, \ldots,n[/math] — координаты вектора [math]\mathbf{b_i}[/math], для [math]\left.i=1,2, \ldots,k\right)[/math], причем [math]\mathbf{b_1}=\mathbf{a_1}[/math], либо

[math]k[/math] ортонормированных векторов [math]\mathbf{q_1},\mathbf{q_2},\ldots,\mathbf{q_k}[/math] длины [math]n[/math] ([math]\gamma_{ij}[/math], [math]j=1,2, \ldots,n[/math] — координаты вектора [math]\mathbf{e_i}[/math], для [math]\left.i=1,2, \ldots,k\right)[/math], причем [math]\mathbf{e_i}=\frac{\mathbf{a_i}}{|\mathbf{a_i}|}[/math], для [math]i=1,2, \ldots,k[/math].

Последовательность исполнения метода:

1. [math]len(a_1)=\sqrt{\alpha_{11}^2+\alpha_{12}^2+\ldots+\alpha_{1n}^2}[/math].

2. При [math]i[/math] от [math]1[/math] до [math]n[/math]:

[math]\gamma_{1j}= \frac{\alpha_{1j}}{len(a_1)}[/math].

3. При [math]i[/math] от [math]2[/math] до [math]k[/math]:

при [math]j[/math] от [math]1[/math] до [math]n[/math]:

[math]\beta_{ij}=\alpha_{ij}-\sum\limits_{k=1}^{j-1}\left(\sum\limits_{m=1}^n \alpha_{im}\varepsilon_{km}\right)\varepsilon_{kj} [/math]

[math]len(b_i)=\sqrt{\beta_{i1}^2+\beta_{i2}^2+\ldots+\beta_{in}^2}[/math]

при [math]j[/math] от [math]1[/math] до [math]n[/math]:

[math]\gamma_{ij}= \frac{\beta_{ij}}{len(b_{i})}[/math].

1.5 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма составляется из вычисления [math]\dfrac{n(n+1)}{2}[/math] скалярных произведений векторов, а также [math]\dfrac{n(n-1)}{2}[/math] умножений векторов на число после вычисления нового базисного вектора на итерации.

1.6 Последовательная сложность алгоритма

Для ортогонализации [math]n[/math] линейно независимых векторов длины [math]n[/math] в последовательном варианте с помощью классического метода ортогонализации Грама-Шмидта потребуется:

• [math]k[/math] вычислений квадратного корня
• [math]\frac{k(k-1)(n-1)}{2}[/math] сложений,
• [math]\frac{k(k-1)(n-1)}{2}[/math] вычитаний,
• [math]k^2 n[/math] умножений,
• [math]k[/math] делений.

Умножения, сложения и вычитания составляют основную часть алгоритма.

При классификации по последовательной сложности, таким образом, метода ортогонализации Грама-Шмидта с кубической сложностью.

1.7 Информационный граф

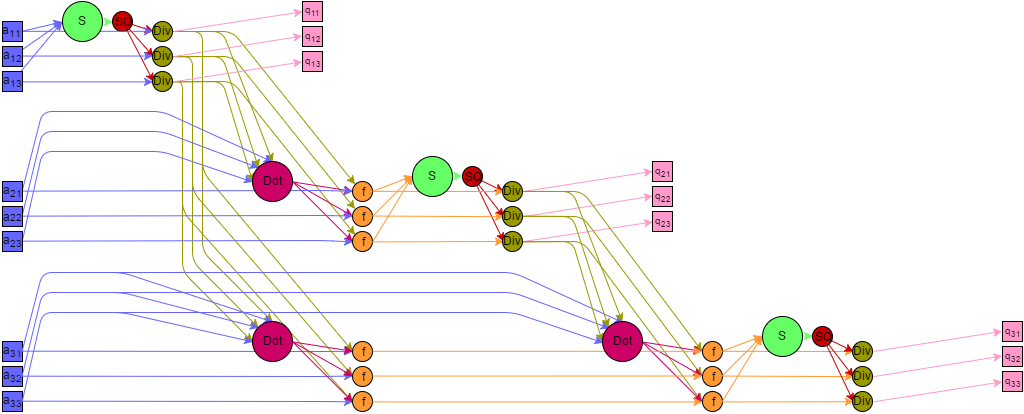
Представим граф алгоритма с помощью текстового описания, а также с помощью изображения.

Все вершины графа можно разбить на шесть групп, каждой из которых соответствует вид исполняемой операции. Каждая вершина расположена в точках с целочисленными координатами, в пространствах с числом измерений от [math]1[/math] до [math]4[/math]. Дадим описание каждой из групп. Поскольку традиционно орт третьей оси имеет обозначение [math]\mathbf{k}[/math], чтобы не путать его с числом [math]k[/math], задающим количество векторов, будем в этом параграфе обозначать количество векторов через [math]m[/math].

Первая группа — вершины, которым соответствует операция возведение в квадрат. На графе они располагаются в двумерной области. [math]i[/math] изменяется от [math]1[/math] до [math]n[/math], [math]k[/math] изменяется от [math]1[/math] до [math]m[/math].

Значениями аргументов для этих функций являются:

• при [math]i = 1[/math] — входные данные [math]a_{1n}[/math];
• при [math]i \gt 1[/math] — результат выполнения функции в вершине шестой группы с координатами [math]i-1,1,\mathbf{k}[/math].

Результат является промежуточным данным алгоритма.

Вторая группа — вершины соответствующие операции сложения, которые проще разбить на две подгруппы, соответствующие четным и нечетным индексам. Они располагаются в четырехмерной области, [math]i[/math] изменяется от [math]1[/math] до [math]2n-1[/math], [math]j[/math] равно [math]1[/math] для нечетных [math]i[/math] и изменяется от [math]2[/math] до [math]n+1-\left\lceil{\dfrac{i}{2}}\right\rceil[/math] для четных [math]i[/math], [math]k[/math] изменяется от [math]1[/math] до [math]\left\lceil{\dfrac{m}{2^{i}}}\right\rceil[/math], [math]t[/math] изменяется от [math]1[/math] до [math]T = \left\lceil{\log_{2}(k)}\right\rceil[/math].

Значениями аргументов для этих функций являются:

• при [math]j = 1, t = 1[/math] — результат выполнения функций в вершинах первой группы с координатами [math](i+1)/2,1,2*k[/math] и [math](i+1)/2,1,2*k - 1[/math];
• при [math]j \gt 1, t = 1[/math] — результат выполнения функции в вершинах пятой группы с координатами [math]i/2,j-1,2*k[/math] и [math]i,j-1,2*k - 1[/math];
• при [math]t \gt 1[/math] — результат выполнения функций в вершинах второй группы с координатами [math]i,j,2*k,t-1[/math] и [math]i,j,2*k-1,t-1[/math] (это точно верно для случаев k являющихся степенью двойки. Для остальных вариантов аргументом может являться результат выполнения функций в вершинах второй группы с последней координатой меньшей чем [math]t-1[/math]).

Результат является промежуточным данным алгоритма.

Третья группа — вершины, которым соответствует операция SQRT извлечения квадратного корня. Они расположены в одномерной области, [math]i [/math]изменяется от [math]1[/math] до [math]n[/math]. Значением аргумента для этих функций является результат выполнения функции в вершине второй группы, с координатами [math]i,1,1,T[/math]

Результат является промежуточным данным алгоритма

Четвертая группа – вершины, которым соответствует операция деления. Располагаются в двумерной области, [math]i[/math] изменяется от [math]1[/math] до [math]n[/math], [math]k[/math] изменяется от [math]1[/math] до [math]m[/math]. Значениями аргументов для этих функций являются:

• делимое:
  • при [math]i = 1[/math] — входные данные [math]a_{1k}[/math];
  • при [math]i \gt 1[/math] — результат выполнения функции в вершине шестой группы с координатами [math]i-1,1,k[/math];
• делитель - результат выполнения функции в вершине третьей группы с координатой [math]i[/math]

Результат является выходным данным алгоритма [math]q_{ik}[/math]

Пятая группа — вершины, которым соответствует операция [math]a*b[/math]. Располагаются в трехмерной области, [math]i[/math] изменяется от [math]1[/math] до [math]n-1[/math], [math]j[/math] изменяется от [math]1[/math] до [math]n-i[/math], [math]k[/math] изменяется от [math]1[/math] до [math]m[/math]. Значениями аргументов для этих функций являются:

• [math]a[/math]:
  • при [math]i = 1[/math] — входные данные [math]a_{1+j,k}[/math];
  • при [math]i \gt 1[/math] — результат выполнения функции в вершине шестой группы с координатами [math]i-1,j+1,k[/math];
• [math]b[/math] — результат выполнения функции в вершине четвертой группы с координатой [math]i[/math]

Результат является промежуточным данным алгоритма

Шестая группа – вершины которые соответствуют операции [math]a - b*c[/math]. Располагаются в трехмерной области, [math]i[/math] изменяется от [math]1[/math] до [math]n-1[/math], [math]j[/math] изменяется от [math]1[/math] до [math]n-i[/math], [math]k[/math] изменяется от [math]1[/math] до [math]m[/math]. Значениями аргументов для этих функций являются:

• [math]a[/math]:
  • при [math]i = 1[/math] — входные данные [math]a_{1+j,k}[/math];
  • при [math]i \gt 1[/math] — результат выполнения функции в вершине шестой группы с координатами [math]i-1,j+1,k[/math];
• [math]b[/math] — результат выполнения функции в вершине второй группы, с координатами [math]i,j+1,1,T[/math]
• [math]c[/math] — результат выполнения функции в вершине четвертой группы с координатой [math]i[/math]

Результат является промежуточным данным алгоритма.

Описанный граф для случая [math]n = 3[/math], [math]k = 4[/math] изображен на рисунке. Каждая группа вершин отличается цветом и буквенным обозначением. "S" — первая группа, "+" — вторая группа, "SQ" — третья группа, "Div" — четвертая группа, "M" — пятая группа, "f" — шестая группа. Квадратные метки "In" и "out" обозначают передачу входных и выходных данных соответственно. Поскольку координаты вдоль оси [math]k[/math] в большинстве случаев соответствуют номеру компоненты рассматриваемого вектора, для удобства визуализации изменение этой координаты зафиксировано локально в каждой подгруппе вершин с одинаковыми координатами [math]i,j[/math] параллельно оси [math]j[/math].

Рисунок 1. Граф алгоритма с отображением входных и выходных данных

1.8 Ресурс параллелизма алгоритма

Для построения ортонормированного базиса методом Грама–Шмидта необходимо выполнить следующие ярусы операций:

• [math]k[/math] ярусов вычисления квадратов числа (по [math]n[/math] операций на каждом);
• [math](2k-1)\left(\left\lceil{\log_{2}(n)}\right\rceil\right)[/math] ярусов суммирования (от [math]1[/math] до [math]\;(k-1)\cdot\dfrac{n}{2}\;[/math] операций на каждом);
• [math]k[/math] ярусов вычисления квадратного корня (по одной операции на каждом);
• [math]k[/math] ярусов деления( по [math]k[/math] операций на каждом);
• [math]k-1[/math] ярус умножения пары чисел (от [math]n[/math] до [math](k-1)n[/math] операций на каждом);
• [math]k-1[/math] ярус умножения/вычитания чисел (от [math]n[/math] до [math](k-1)n[/math] операций на каждом).

В этом случае сложность алгоритма при классификации по высоте ЯПФ — [math]O(k\log{n})[/math], при классификации по ширине ЯПФ — [math]O(kn)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: матрица [math]A[/math] с элементами [math]\alpha_{ij}[/math], где [math]i[/math] принимает значения [math]1,\ldots,k[/math], [math]j[/math] принимает значения [math] 1,\ldots,n[/math]. Здесь [math]k\leqslant n[/math]. По строкам этой матрицы записаны [math]k[/math] линейно-независимых векторов некоторого пространства размерности [math]n[/math].

Объем входных данных: [math]kn[/math].

Выходные данные: матрица [math]Q[/math] с элементами [math]\gamma_{ij}[/math]. Строки этой матрицы также задают [math]k[/math] векторов единичной длины размерности [math]n[/math], причем всякое скалярное произведение двух различных векторов этой системы равно [math]0[/math].

Объем выходных данных: [math]kn[/math].

Замечание: Алгоритм может работать с вырожденной матрицей, он выдаёт нулевую строку на шаге [math]j[/math], если строка [math]j[/math] матрицы [math]A[/math] является линейной комбинацией предыдущих строк. В этом случае для корректного продолжения работы алгоритма необходима дополнительная проверка на равенство строки нулю и пропуск соответствующих строк. Количество построенных векторов будет равняться размерности пространства, порождаемого строками матрицы.

1.10 Свойства алгоритма

Отношение последовательной и параллельной сложности алгоритма в случае неограниченных ресурсов равно [math]\dfrac{k^2n}{k\log{n}}=\dfrac{kn}{\log{n}}[/math]. Вычислительная мощность алгоритма линейная.

Алгоритм почти полностью детерминирован — единственность результата выполнения гарантирована, однако возможно накопление ошибок округления.

Алгоритм является численно неустойчивым — ошибки округления могут привести к неортогональности полученных векторов.

Большинство дуг информационного графа являются локальными. Исключение составляют дуги исходящие из операций деления и извлечения корня — для первой группы количество дуг пропорционально квадрату количества векторов, а для второй — пропорционально размерности пространства, в котором заданы эти вектора. Возникающие при это длинные дуги могут быть заменены несколькими короткими пересылками между соседями.

2 ЧАСТЬ Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Срок сдачи продлён до 15-го ноября.

2.7 Существующие реализации алгоритма

Для классического метода ортогонализации Грама–Шмидта существуют реализации в математических программных пакетах, таких как Matlab, Maxima, Mathematica. Также метод реализован в библиотеке SpectralPython для языка Python. Для устранения проблемы ошибок численных округлений иногда используется повторное применение метода к уже построенному ортогональному базису.

Поскольку гарантирует получение [math]j[/math] ортогональных векторов к концу шага [math]j[/math], а не в самом конце работ алгоритма, используется в итерационных методах таких как метод Арнольди. Для поддержки работы этого метода реализация ортогонализации Грама-Шмидта включена в библиотеку ARPACK.