Участник:Alexander34396/Обобщенный метод минимальных невязок

Эта работа ждет рассмотрения преподавателем Дата последней правки страницы: 18.10.2016 Авторы этой статьи считают, что задание выполнено.

Основные авторы описания: А.А.Ульянов (разделы 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.9, 2.7), К.Петров (разделы 1.7, 1.8, 1.10, 2.4).

Обобщенный метод минимальных невязок
Последовательный алгоритм
Последовательная сложность	[math] O(nm^2) [/math]
Объём входных данных	[math] (n + 1)^2 [/math]
Объём выходных данных	[math] n [/math]

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Обобщённый метод минимальных невязок (англ. Generalized minimal residual method, GMRES) - итерационный метод численного решения системы линейных алгебраических уравнений с невырожденной матрицей. Метод основан на минимизации квадратичного функционала невязки на подпространствах Крылова. Разработан Юсефом Саадом и Мартином Шульцем в 1986 году как обобщение метода MINRES на случай систем с несимметричными матрицами.

1.2 Математическое описание алгоритма

Исходные данные:

• система линейных алгебраических уравнений вида [math] Ax = b [/math], где [math] A [/math] — невырожденная матрица размера [math]n[/math]-на-[math] n [/math];
• [math] x_0 [/math] - начальное приближение.

Вычисляемые данные:

• [math] x_m [/math] - приближённое решение исходной системы.

Метод GMRES приближает точное решение исходной системы [math] Ax = b [/math] вектором [math] x_m [/math], который минимизирует [math] l_2 [/math]-норму невязки [math] r_m = Ax_m - b[/math] на подпространстве Крылова:

[math] K_m = K_m(A,b) = \operatorname{span} \, \{ b, Ab, A^2b, \ldots, A^{m-1}b \} [/math].

На каждой итерации метода решение уточняется поправкой, представленной в виде разложения по [math] l_2 [/math]-ортонормированному базису пространства [math] K_m [/math]:

[math] x_m = x_0 + z_m [/math], где [math] x_0 [/math] - некоторое начальное приближение, [math] z_m \in K_m [/math] - поправка решения.

1.2.1 Ортогонализация Арнольди

Для построения ортонормированного базиса [math] K_m [/math] метод использует процесс Арнольди.

Исходные данные:

• [math] v_1 [/math], такой что [math] \|v_1\|_2 = 1 [/math];
• матрица [math] A [/math] размером [math] n [/math]-на-[math] n [/math].

Формула процесса:

[math] h_{j+1j}v_{j+1} = Av_j - \sum_{i=1}^j h_{ij}v_{j} [/math], где [math] h_{ij} = (Av_j, v_i)[/math], [math] \quad j=1,\ldots,m [/math].

Алгоритм процесса:

Выполнять для [math] \quad j=1,\ldots,m [/math]:

1. [math] h_{ij} = (Av_j, v_i), \quad i=1,\ldots,j [/math];
2. [math] \hat{v}_{j+1} = Av_j - \sum_{i=1}^j h_{ij}v_{i} [/math];
3. [math] h_{j+1j} = \|\hat{v}_{j+1}\|_2 [/math];
4. [math] v_{j+1} = \frac{\hat{v}_{j+1}}{h_{j+1j}} [/math].

При введении матричных обозначений можно записать:

1. [math] z_m = V_my_m [/math], где [math] y_m \in \mathbb{R}^m [/math] - вектор коэффициентов;
2. [math] AV_m = V_mH_m + h_{m+1m}v_{m+1} e_m^T = V_{m+1}\overline{H}_m [/math], где [math] V_m = [v_1|v_2|...|v_m] [/math], а [math] \overline{H}_m [/math] - верхняя матрица Хессенберга размерности [math] (j+1) [/math] на [math] j [/math].

1.2.2 Минимизация функционала невязки

Для решения исходной системы GMRES вычисляет приближённое решение [math] x_m [/math], которое минимизизует функционал невязки:

[math] J(y) = \|b- A x_m\|_2 = \|b - A(x_0 + V_my)\|_2 = \|\beta e_1 - \overline{H}_my_m \|_2 [/math], где [math] \beta = \|r_0\|_2 [/math].

Вектор [math] y_m [/math] может найден как решение линейной задачи наименьших квадратов размера [math] m+1 [/math]-на-[math] m [/math]:

[math] y_m = \arg\min_{y}\| \beta e_1 - \overline{H}_my\|_2 [/math].

Для решения задачи матрица [math] \overline{H}_m [/math] приводится к верхнему треугольному виду с помощью [math] m [/math] последовательных вращений Гивенса.

1.2.3 Общая схема метода

В общем виде m-aя итерация алгоритма GMRES может быть записан следующим образом:

1. найти ортонормированный базис [math] V_m [/math] подпространства [math] K_m [/math] с помощью ортогонализации Арнольди;
2. найти [math] y_m [/math], минимизирующий [math] \|r_m\|_2 [/math];
3. вычислить [math] x_m = x_0 + V_my_m [/math], где [math] x_0 [/math] - начальное приближение;
4. вычислить [math] r_m [/math] и остановиться,если требуемая точность была достигнута, иначе повторить.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро последовательной версии метода GMRES состоит из двух частей:

• Вычисление ортонормированного базиса [math] K_m [/math];
• Формирование приближенного решения [math] x_m [/math].

Для вычисления ортонормированного базиса [math] K_m [/math] метод использует процесс Арнольди:

[math] h_{j+1j}v_{j+1} = Av_j - \sum_{i=1}^j h_{ij}v_{j} [/math], где [math] h_{ij} = (Av_j, v_i)[/math], [math] \quad j=1,\ldots,m [/math].

Для нахождения приближённого решения [math] x_m [/math] метод использует формулу:

[math] x_m = x_0 + V_my_m [/math].

1.4 Макроструктура алгоритма

В алгоритме можно выделить следующие макрооперации:

• Умножение матрицы на вектор;
• Вычисление скалярного произведения векторов;
• Вычисление [math] l_2 [/math]-нормы вектора;
• Умножение вектора на скаляр;
• Деление вектора на скаляр.

1.5 Схема реализации последовательного алгоритма

На практике используется перезапускаемая версия метода - GMRES(m):

1 Подготовка перед итерационным процессом:

1.1 Выбрать начальное приближение [math] x_0 [/math];

1.2 Посчитать невязку [math] r_0 = b - Ax_0 [/math];

1.3 Вычислить [math] v_1 = \frac{r_0}{\|r_0\|_2} [/math].

2 Построение ортонормированного базиса [math] K_m [/math]:

Для всех [math] j [/math] от 1 до m по нарастанию выполнять:

2.1 [math] h_{ij} := (Av_j, v_i), \quad i=1,\ldots,j [/math];

2.2 [math] \hat{v}_{j+1} := Av_j - \sum_{i=1}^j h_{ij}v_{i} [/math];

2.3 [math] h_{j+1j} = \|\hat{v}_{j+1}\|_2 [/math];

2.4 [math] v_{j+1} = \frac{\hat{v}_{j+1}}{h_{j+1j}} [/math].

3 Вычисление [math] x_m [/math]:

3.1 [math] x_m = x_0 + V_my_m [/math], где [math]y_m[/math] минимизирует [math]\|r_0 - AV_my_m\|_2[/math];

3.2 Вычислить [math] r_m [/math];

3.3 Если требуемая точность достигнута, остановиться.

4 Перезапуск:

4.1 [math]x_0 = x_m[/math];

4.2 [math]v_1 = \frac{r_m}{\|r_m\|_2}[/math];

4.3 Перейти к шагу 2.

1.6 Последовательная сложность алгоритма

Если пренебречь сложностью вычисления [math] y_m [/math], то общую сложность алгоритма GMRES можно разделить на две части:

1. Сложность вычисления ортонормированного базиса пространства [math] K_m [/math]:

a) Для вычисления [math] j [/math]-го вектора базиса [math] K_m, j \lt m [/math] требуется:

[math] NZ + (2j + 1)n [/math] мультипликативных операций, где [math] NZ [/math] - количество ненулевых элементов матрицы [math] A [/math].

b) Вычисление последнего вектора базиса требует:

[math] n(m + 1) [/math] мультипликативных операций.

c) Общая мультипликативная сложность вычисления ортонормированного базиса [math] K_m [/math]:

[math] O(nm^2) [/math].

2. Сложность вычисления приближённого решения [math] x_m [/math]:

a) Вычисление этой формулы требует [math] nm [/math] мультипликативных операций.

1.7 Информационный граф

---

---

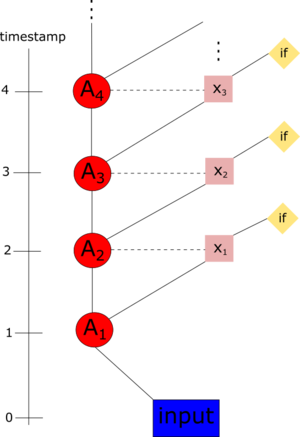
На информационном графе:

• input - входные данные алгоритма (квадратная матрица, вектор правой части, начальное приближение, точность решения);
• [math] A_i [/math] - шаги алгоритма Арнольди, [math] x_i [/math] - нахождение невязки на [math] i [/math]-ой итерации;
• if - вычисление [math] r_m [/math] и в случае достижения нужной точности - остановка.

При этом, шаги алгоритма Арнольди выполняются строго последовательно, но вычисление [math] i [/math]-ой невязки может происходить параллельно с [math] (i + 1) [/math]-ым шагом алгоритма Арнольди.

1.8 Ресурс параллелизма алгоритма

В ходе анализа перезапускаемого метода обобщенных минимальных невязок был выявлен ряд подзадач, выполняющихся неоднократно: умножение матрицы на вектор, вычисление скалярного произведения векторов, нахождение нормы вектора, нормирование вектора, нахождение взвешенной суммы векторов. Наиболее трудоемкой среди перечисленных операций является умножение матрицы на вектор.

Выполнение перечисленных операций занимает большую часть времени работы алгоритма GMRES. Поэтому при увеличении эффективности использования вычислительных ресурсов и ресурсов памяти вычислительной машины при выполнении этих операций повышается эффективность метода в целом. Достигается это применением при выполнении перечисленных операций аппарата параллельных вычислений.

При выполнении параллельного алгоритма решения систем линейных алгебраических уравнений необходимо распределить входные данные наиболее рациональным способом. Матрица коэффициентов разбивается на непрерывные горизонтальные полосы. Распределение вектора правой части и начального приближения выполнено по принципу дублирования, т.е. все элементы векторов скопированы на все процессоры. Для рассматриваемой задачи решения СЛАУ такой подход распределения допустим, т.к. векторы содержат столько же элементов, сколько и одна строка или один столбец матрицы коэффициентов.

Подзадачи можно разделить на 2 группы: операции между матрицей и вектором (например, умножение матрицы на вектор) и операции между двумя векторами (например, скалярное умножение). Подзадачи умножения константы на вектор и определение нормы вектора можно относить ко второй группе, так как их трудоемкость одного порядка.

Результатом выполнения рассматриваемых операций является, вектор, части которого расположены на участвовавших в вычислениях процессорах. Для объединения результатов расчета и получения полного вектора на каждом процессоре вычислительной системы необходимо выполнить операцию сбора данных.

1.9 Входные и выходные данные алгоритма

Входные данные:

• [math] A [/math] – квадратная матрица размера [math] n [/math]-на-[math] n [/math];
• [math] b [/math] – вектор правой части размера [math] n [/math];
• [math] x_0 [/math] – начальное приближение размера [math] n [/math];
• [math] \epsilon [/math] – погрешность решения.

Для перезапускаемой версии алгоритма дополнительно:

• [math] m [/math] – число итераций.

Объём входных данных: [math] n^2 + 2n + 1 [/math].

Выходные данные:

• [math] x_m [/math] - вектор приближённого решения размера [math] n [/math].

Объём выходных данных: [math] n [/math].

1.10 Свойства алгоритма

Вычислительная схема требует работы со следующими объектами: разреженной матрицей исходной СЛАУ — [math]n + 2k [/math] вещественных и [math] n + k + 1 [/math] целых (причем обычно двойной длины!) чисел; векторами правой части, искомого решения и невязки — [math]3n[/math] вещественных чисел; векторами базиса подпространства Крылова — [math] mn [/math] вещественных чисел; плотной матрицей малой переопределенной СЛАУ — [math] m(m + 1) [/math] вещественных чисел; коэффициентами вращений Гивенса — [math] 2m [/math] вещественных чисел; вектором решения малой СЛАУ (как с коэффициентами линейного комбинирования векторов базиса подпространства Крылова) — [math] m [/math] вещественных чисел.

Полагая объем памяти для счетчиков циклов и временных переменных скалярного типа пренебрежимо малым, можно получить, что всего требуется хранить [math] n + k + 1 [/math] целых чисел двойной длины и [math]4n + 2k + mn + (m + 1)2 + 3m + 1[/math] — вещественных. При использовании обычной точности это требует [math]20n+12k+4mn+4(m+1)2+12m+8[/math] байт, двойной — [math]36n + 20k + 8mn + 8(m + 1)2 + 24m + 16[/math] байт. С учетом того, что [math]1 \lt m \ll n [/math] и [math] k \ll n [/math], можно говорить, что требования метода GMRES к объему доступной памяти составляют [math] O(mn) [/math].

Основные вычислительные затраты определяются операциями нахождения скалярных произведений и линейного комбинирования векторов. Эти действия требуют [math] 2n^3 + \frac {3}{2}n^2- \frac{1}{2}n [/math] арифметических операций. Доля соответствующих вычислительных затрат в схеме метода, таким образом, равна [math] \frac {2n^3 + \frac {3}{2}n^2- \frac{1}{2}n}{2n^3 + 7n^2 + 3n} [/math], т. е. при больших размерностях СЛАУ близка к 1.

При этом строки матрицы СЛАУ, начиная с первой, последовательно исключаются из процесса решения. В такой ситуации наиболее эффективной является параллелизация, основанная на столбцовой декомпозиции матрицы СЛАУ при реализации вычислений на топологии межпроцессорных соединений “каждый с каждым”. При этом работу с вектором правой части целесообразно дублировать на каждом из процессоров. При использовании такой схемы на [math]p[/math] процессорах число арифметических действий, выполняемых одним процессором, сокращается до величины [math] N^A_p(n) = \frac {n(3n^2+2n+np+p+1)}{p} [/math].

В вычислительной схеме GMRES присутствуют два интенсивных в вычислительном плане этапа: умножение матрицы СЛАУ на вектор (для нахождения невязок) и нахождение скалярных произведений векторов (при построении ортонормального базиса подпространства Крылова). Кроме того, именно на хранение векторов базиса [math] \left \{ v_j \right \} [/math] в GMRES приходится бОльшая часть затрат памяти ( [math] mn [/math] вещественных чисел, что часто оказывается больше объема памяти под разреженную матрицу СЛАУ). При этом в GMRES-схеме присутствует достаточно самостоятельная подзадача — решение переопределенной СЛАУ малой размерности в смысле наименьших квадратов, которая должна рассматриваться отдельно.

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

Реализации алгоритма GMRES присутствуют во многих программных пакетах:

• LINPACK
• JAMA/C++
• ATLAS
• Intel MLK
• IML++
• LAPACK
• MTL
• SPARSKIT
• WSMP

3 Литература

<references \>