Участник:MukhayevD/Метод Ньютона

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня заданной функции(в связи с трудностями программирования производной для произвольной функции рассматриваются только функции в виде полинома). Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Модификацией метода является метод хорд и касательных.

1.2 Математическое описание алгоритма

Пусть [math] x_n [/math] - некоторое приближение к корню уравнения [math] f(x) = 0, f \in C^1 [/math], то следующее приближение определяется как корень касательной к функции [math] f(x) [/math], проведенной в точке [math] x_n [/math].

Уравнение касательной к функции [math] f(x) [/math] в точке [math] x_n [/math] имеет вид: [math] f^'(x_n) = (y - f(x_n))/(x - x_n) [/math] В уравнении касательной положим [math] y = 0 [/math] и [math] x = x_{n+1} [/math]. Тогда алгоритм последовательных вычислений в методе Ньютона состоит в следующем: [math] x_{n+1} = x_n - f(x_n)/f^'(x_n) [/math] Сходимость метода касательных квадратичная, порядок сходимости равен 2.

1.3 Вычислительное ядро алгоритма

Основная вычислительная нагрузка алгоритма заключается в нахождении [math] \varphi(x_n) = f(x_n)/f^'(x_n) [/math], которая в последствии используется для нахождения [math] x_{n+1} = x_n - \varphi(x_n) [/math]

1.4 Макроструктура алгоритма

Как и было описано в описании ядра алгоритма, основную часть метода составляет вычисление значения функции [math] f(x_n) [/math] и ее производной [math] f^'(x_n) [/math] в точке x_n.

[math] f(x_n) = \sum_{i=0}^{n}f_ix_n^i [/math]

[math] f^'(x_n) = \sum_{i=0}^{n-1}f^'_ix_n^i [/math]

1.5 Схема реализации последовательного алгоритма

Последовательность исполнения метода следующая:

 1. Выбираем начальное приближение [math] x_0 [/math]
 2. Находим значение функции [math] f(x_n) [/math] в точке [math]x_n[/math].
 3. Находим значение производной функции [math] f^'(x_n) [/math] в точке [math]x_n[/math].
 4. Получаем следующий шаг итерации [math] x_{n+1} [/math][math] x_{n+1} = x_n - f(x_n)/f^'(x+n) [/math]
 5. Находим погрешность [math] e = |x_{n+1} - x_n| [/math]
 6. Если погрешность не превышает некоторого заранее заданного числа - останавливаемся.

[math] e \lt \varepsilon [/math]

1.6 Последовательная сложность алгоритма

Для вычисления корня методом Ньютона при последовательном выполнении требуется:

• [math] n [/math] сложение + [math] n [/math] умножений + [math] n-1 [/math] умножений (возведение в степень)

• [math] n-1 [/math] сложение + [math] n-1 [/math] умножений + [math] n-2 [/math] умножений (возведение в степень)

• одно вычитание и одно деление

• одно вычитание

Следовательно для одного шага алгоритма требуется:

• [math] 2n-1 [/math] сложение (вычитание)
• [math] 4n-3 [/math] умножений (делений)

1.7 Информационный граф

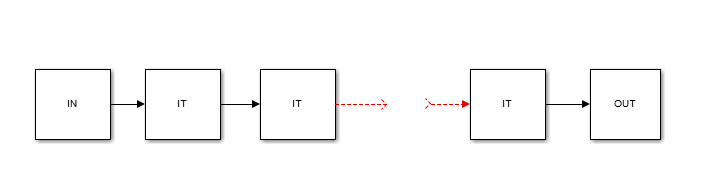
На рисунке ниже изображена структура информационного графа алгоритма. Блок IN представляет собой выбор начального приближения, блок IT - итерацию алгоритма, блок OUT - концу работы алгоритма.

Рисунок 1. Информационный граф

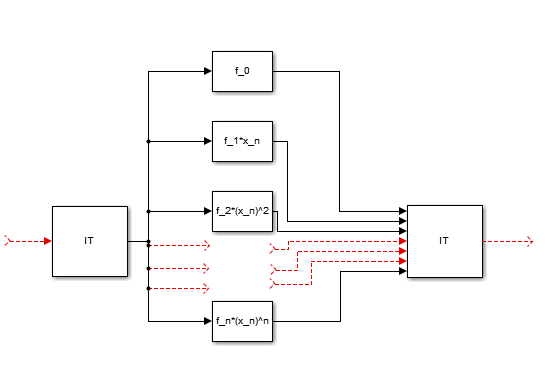
Как видно, алгоритм строго последовательный. Ниже подробнее рассмотрено как можно разделить нагрузку связанную с вычислениями [math] f(x) [/math] между процессорами. Каждое слагаемое полинома считается отдельно.

Рисунок 2. Итерация

Аналогично для [math] f^'(x) [/math].

1.8 Ресурс параллелизма алгоритма

Несмотря на то, что сам по себе алгоритм является строго последовательным, его можно ускорить за счет распараллеливания нахождения функции и ее производной на текущей итерации, так как это было описано в предыдущем пункте.

Пусть имеем [math] p [/math] процессоров, в таком случае каждому процессору нужно будет произвести [math] (4n-3)/p [/math] умножений.

1.9 Входные и выходные данные алгоритма

Входными данными алгоритма являются:

  1. Функция в виде полинома.
  2. Область, в которой ищется корень [math] (a;b) [/math].
  3. Начальное приближение [math] x_0 [/math].
  4. Точность, с которой требуется найти решение.

На выход алгоритмом выдается число - предположительный корень найденный с заданной точностью.

2 Программная реализация алгоритма

2.1 Масштабируемость алгоритма и его реализации

Так как сам по себе метод является последовательным то, следовательно о его масштабируемости не может быть и речи.

Поверка масштабируемости реализации метода проводилась на следующих тестах:

• 1) [math] (x-1)g(x) [/math], где [math] g(x) [/math] - произвольный полином степени [math] n-1 [/math].

Рисунок 1.

• 2) [math] 1 + 2x + 2x^2 + ... + 2x^{n-1} + x^n [/math]

Рисунок 2.

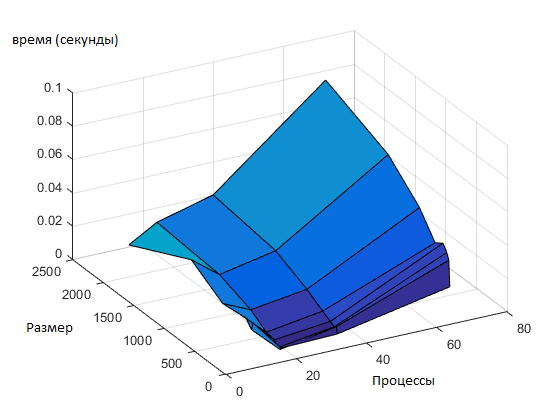
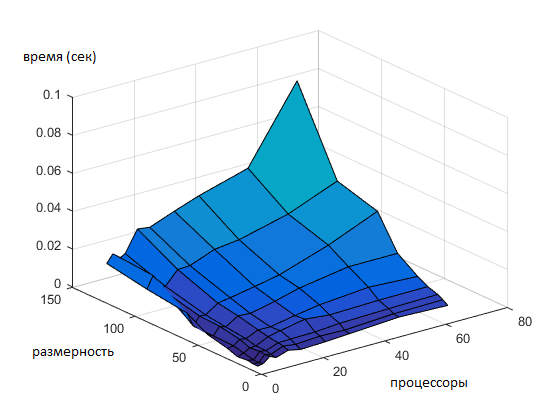
Как видно из рисунков вне зависимости от размерности задачи не удалось добиться времени больше [math] 0.1 [/math] секунды, в виду этого можно предположить, что время зависит от физического расположения процессоров, но тем не менее есть общая тенденция, что время работы возрастает вместе с размерностью и количеством процессоров.

2.2 Существующие реализации алгоритма

1. Последовательные реализации

• • ALIAS C++. Язык реализации - C++. Распространяется бесплатно, исходные коды и примеры использования можно скачать на сайте.
  • Numerical Recipes. Язык реализации - C++. Исходный код можно найти в секции 9.7 книги Numerical recipes(third edition). Бесплатно доступны предыдущие издания для языков C, Fortran77, Fortran90.
  • Sundials. Язык реализации - C, также есть интерфейс для использования в Fortran-программах. Распространяется по лицензии BSD.

2. Параллельные реализации

• • Построение параллельной реализации метода Ньютона для решения задач линейного программирования описано в работе В.А. Гаранжа, А.И. Голикова, Ю.Г. Евтушенко, М.Х. Нгуена "Параллельная реализации метода Ньютона для решения больших задач линейного программирования" .
  • Построение параллельной реализации метода Ньютона для решения задач оптимизации, описываются в работе V. A. Garanzha, A. I. Golikov, Yu. G. Evtushenko, and M. Kh. Nguen "Parallel Implementation of Newton’s Method for Solving Large-Scale Linear Programs" .
  • Построение параллельной реализации метода Ньютона, а также результаты некоторых экспериментов, описываются в работе Renato N. Elias Alvaro L. G. A. Coutinho Marcos A. D. Martins Rubens M. Sydenstricker "PARALLEL INEXACT NEWTON-TYPE METHODS FOR THE SUPG/PSPG SOLUTION OF STEADY INCOMPRESSIBLE 3D NAVIER-STOKES EQUATIONS IN PC CLUSTERS" .
  • Описание использования и результатов экспериментов с параллельной реализацией метода Ньютона в задаче фильтрации вязкой сжимаемой многофазной многокомпонентной смеси в пористой среде описано в работе К.Ю.Богачева "Эффективное решение задачи фильтрации вязкой сжимаемой многофазной многокомпонентной смеси на параллельных ЭВМ".

3 Литература

<references \>