Алгоритм Ланцоша с выборочной ортогонализацией

Эта работа ждет рассмотрения преподавателем
Дата последней правки страницы: 19.12.2016
Авторы этой статьи считают, что задание выполнено.

Авторы: Беслаев М.Н. 619, Тевдорадзе С.З. 614. Авторы внесли равнозначный вклад в каждый из разделов данной статьи.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм Лáнцоша представляет собой мощный метод для нахождения нескольких собственных значений и собственных векторов симметричной матрицы А и для решения систем линейных уравнений. Алгоритм особенно эффективен, если матрица А разреженная и большого размера. Однако любая практическая реализация этого алгоритма страдает от ошибок округления, т.к. векторы Ланцоша теряют взаимную ортогональность. Для того чтобы поддерживать некоторый уровень ортогональности, появились методы полной переортогонализации и выборочной ортогонализации. В этой работе мы рассмотрим последний метод в качестве способа для поддержания ортогональности среди векторов Ланцоша. Он обладает почти столь же высокой точностью, как алгоритм с полной переортогонализацией, и почти столь же низкой стоимостью, как алгоритм без ортогонализации ^[1].

Дается вещественная симметричная матрица [math]A = A^T[/math],

[math] A = \begin{pmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1\ n-1} & a_{1\ n} \\ a_{12} & a_{22} & a_{23} & \cdots & a_{2\ n-1} & a_{2\ n} \\ a_{13} & a_{23} & a_{33} & \cdots & a_{3\ n-1} & a_{3\ n} \\ \vdots & \vdots & \ddots & \ddots & \ddots & \vdots \\ a_{1\ n-1} & \cdots & \cdots & a_{n-2\ n-1} & a_{n-1\ n-1} & a_{n-1\ n} \\ a_{1\ n} & \cdots & \cdots & a_{n-2\ n} & a_{n-1\ n} & a_{n\ n} \\ \end{pmatrix} [/math] [math] \, \; (1), [/math]

случайный вектор [math]b [/math], являющийся первым приближением собственного вектора матрицы, [math]k [/math] - количество собственных значений и собственных векторов, которые мы хотим найти, т.е. количество итераций.

На каждой итерации строится матрица [math]Q_j = [q_1, q_2, \dots, q_j][/math] размерности [math]n \times j[/math], состоящая из ортонормированных векторов Ланцоша [math]z[/math]. В качестве приближенных собственных значений берутся числа Ритца [math]\theta_i [/math], т.е. собственные значения симметричной трехдиагональной матрицы [math]T_j = Q^T_j A Q_j[/math] размерности [math]j \times j[/math].

[math] T_j = \begin{pmatrix} \alpha_1 & \beta_1 \\ \beta_1 & \alpha_2 & \beta_2 \\ & \beta_2 & \ddots & \ddots \\ & & \ddots & \ddots & \beta_{j-1} \\ & & & \beta_{j-1} & \alpha_j \end{pmatrix}\; (2). [/math]

Однако, векторы [math]q_j [/math] теряют ортогональность вследствие приобретения больших компонент в направлениях векторов Ритца [math]y_{i,j} = Q_j v_i [/math], отвечающих сошедшимся числам Ритца [math] \theta_i [/math]. Поэтому чтобы построить [math]q_j [/math], предлагается на каждом шаге следить за оценками погрешностей [math]\beta_{t}|v_i(t)|, i = 1 \dots t, t = j - 1 [/math], где [math]v_i(t) [/math] - [math]t[/math]-я компонента собственного вектора [math]v_i [/math]. И когда какая-то оценка становится слишком малой, проводить ортогонализацию вектора Ланцоша [math]z [/math]. Величина [math]\beta_{t}|v_i(t)| [/math] считается малой, если она меньше, чем [math]\sqrt{\varepsilon}||T_{t}|| [/math], где [math]\varepsilon[/math] - доступная машинная точность чисел.

После следует вычисление собственных значений [math] \theta_j [/math] и собственных векторов [math]v_j [/math] полученной трехдиагональной матрицы [math]T_j[/math], для чего существует, например, метод "разделяй и властвуй"^[2]

1.2 Математическое описание алгоритма

[math] \beta_0=0,q_0=0[/math]
[math] q_{1} = \frac{b_{j}}{\|b\|_2}[/math], где [math] \|b\|_2 = \sqrt{\sum\limits_{j=1}^{n} b_j^2}[/math]
[math] for\, j=1\,\, to\, \, k\, \, do:[/math]
    [math]z=Aq_j,  [/math]
    [math]\alpha_j=q_j^Tz, [/math]
    [math]z=z-\alpha_jq_j-\beta_{j-1}q_{j-1},  [/math]
    [math]t = j - 1,  [/math]
    [math]for\, i=1\,\, to\, \, t\, \, do: [/math]
        [math]if\,  \beta_{t}|v_i(t)| \leqslant \sqrt{\varepsilon}\|T_{t}\| \, \,  then:[/math]
            [math]z = z-(y^T_{i,t},z)y_{i,t} [/math], где [math]y_{i,t} = Q_{t}v_i[/math] 
    [math]\beta_{j}=\|z\|_2 [/math]
    [math]q_{j+1}=z/\beta_{j}, [/math]
    Строим матрицу  [math] T_j[/math] (2), вычисляем собственные значения  [math] \theta_j [/math] и собственные векторы [math]v_j [/math] полученной матрицы [math]T_j[/math].

1.3 Вычислительное ядро алгоритма

Выделены следующие вычислительные ядра:

Умножение матрицы на вектор, [math]z=Aq_j, [/math].

Ортогонализация по отношению к сошедшимся векторам [math]z = z-(y^T_{i,t},z)y_{i,t} [/math] для [math]i = 1 \dots t[/math]

1.4 Макроструктура алгоритма

Были выделены следующие макрооперации:

1. Умножение матрицы на вектор,

[math]z=Aq_j, [/math].

2. Вычисление вектора [math]q_{j+1} [/math] с помощью линейной комбинации других векторов:

[math]\alpha_j=q_j^Tz, [/math]

[math]z=z-\alpha_jq_j-\beta_{j-1}q_{j-1}, [/math]

[math]q_{j+1}=z/\|z\|_2[/math]

3. Ортогонализация вектора Ланцоша с помощью скалярного произведения:

[math]z = z-(y^T_{i,t},z)y_{i,t} [/math]

4. Для вычисления собственных значений матрицы будет использоваться алгоритм "разделяй и властвуй".

1.5 Схема реализации последовательного алгоритма

[math]1)[/math] Инициализируются векторы [math] \beta_0=0,q_0=0,[/math]
[math]2)[/math] Считается норма вектора [math] b: \; \;  \|b\|_2 = \sqrt{\sum\limits_{j=1}^{n} b_j^2},[/math]
[math]3)[/math] Находится первый вектор матрицы [math] Q: \; \; q_{1} = \frac{b_{j}}{\|b\|_2},[/math]
[math]4)[/math] Начинается цикл, повторяющийся [math] k [/math] раз по переменной [math] j: [/math]
   [math]4.1)[/math] Считается произведение матрицы на вектор: [math] z_d = \sum\limits_{y=1}^{n} a_{dy} q_{j_y}, \; d = 1,\,\dots\,, n, [/math] где 
   [math]z_d - [/math] компоненты вектора Ланцоша [math]z, [/math]
   [math]4.2)[/math] Скалярно умножается [math]q_j^T[/math]  и [math] z: \; \; \alpha_j = \sum\limits_{d=1}^{n}q_{j_d} z_d,[/math]
   [math]4.3)[/math] Вычисляется линейная комбинация векторов [math]z=z-\alpha_jq_j-\beta_{j-1}q_{j-1},  [/math]
   [math]4.4)[/math] [math]t[/math] Присваивается [math]j - 1.  [/math] В цикле по [math] i [/math] от первого до посчитанного [math] t[/math]-го собственного вектора проводится
   выборочная ортогонализация к сошедшимся векторам Ритца. То есть:
      [math]4.4.1)[/math] Считается норма матрицы [math]\|T_{t}\|_2, [/math] [math] \| T \|_2 =  \sup\limits_{\| x \|_2 = 1} \| T x \|_2 = \sup\limits_{(x, x) = 1} \sqrt{(Tx, Tx)}[/math], подчиненная векторной норме [math] \| x \|_2 = \sqrt{\sum_{i = 1}^n |x_i|^2} [/math]. Т.е. 
      [math] \|    T_{t} \|_2 =  \max\limits_{i=1 \dots t} \theta_i[/math], где [math] \theta_i[/math] - собственные значения матрицы [math] T,[/math]
      [math]4.4.2)[/math] Берется [math]t[/math]-ю координата вектора [math] v_i[/math]  и проверяется, выполняется ли равенство:[math]\beta_{t}|v_i(t)| \leqslant \sqrt{\varepsilon}\|T_{t}\| \, \, ,[/math]
      Если выполняется, то
          [math]4.4.2.1)[/math] Ищется вектор Ритца [math]y_{i,t_d} = \sum\limits_{x=1}^{t} q_{x_d} v_{i_x}, \; d = 1,\,\dots\,, n,[/math], где  [math]y_{i,t_d}[/math] -  [math]d[/math]-я компонента вектора Ритца [math]y,[/math]
          [math]4.4.2.2)[/math] Скалярно умножается [math]y_{i,t}^T[/math]  и [math] z: \; \; \gamma = \sum\limits_{d=1}^{n}y_{i,t_d} z_d,[/math]
          [math]4.4.2.3)[/math] Вычисляется линейная комбинация векторов [math]z = z-\gamma\,  y_{i,t}, [/math]
          [math]4.4.2.4)[/math] Увеличивается [math]i [/math]. Производится возврат к пункту [math]4.4.2,[/math]
   [math]4.5)[/math] Ищется норма вектора [math] z: \; \; \beta_{j}=\|z\|_2, [/math]
   [math]4.6)[/math] Ищется вектор Ланцоша [math]q_{j+1}=z/\beta_{j}, [/math]
   [math]4.7)[/math] Вычисляется новое собственное значение [math] \theta_j [/math] и собственный вектор [math] v_j [/math] для полученной матрицы [math] T_j,[/math]
   [math]4.8)[/math] Увеличивается [math] j [/math], производится возврат к шагу [math]4.1.[/math]

1.6 Последовательная сложность алгоритма

Рассмотрим последовательную сложность алгоритма.

[math]1)[/math] Инициализируются векторы,
[math]2)[/math] Считается норма вектора: [math] n [/math] сложений и умножений, одно вычисление корня,
[math]3)[/math] Находится первый вектор матрицы: [math] n [/math] делений,
[math]4)[/math] Начинается цикл, повторяющийся [math] k [/math] раз по переменной : [math]   j [/math]:
   [math]4.1)[/math] Считается произведение матрицы на вектор: [math]   n [/math] сложений и умножений,
   [math]4.2)[/math] Скалярно умножается два вектора : [math]   n [/math] сложений и умножений,
   [math]4.3)[/math] Вычисляется линейная комбинация векторов : [math]   2n [/math] вычитаний и умножений,
   [math]4.4)[/math] Повторяется цикл : [math]   j-1 [/math] раз. На каждом из этапов:
      [math]4.4.1)[/math] Считается норма матрицы: : [math]   j-1 [/math] сравнений,
      [math]4.4.2)[/math] Проверяется равенство::  2 умножения, одно сравнение
          [math]4.4.2.1)[/math] Ищется вектор Ритца : [math]   n*(j-1) [/math] сложений и умножений,
          [math]4.4.2.2)[/math] Скалярно умножаются два вектора:  [math]   n [/math] сложений и умножений,
          [math]4.4.2.3)[/math] Вычисляется линейная комбинация векторов : [math]   n [/math] умножений и вычитаний,
          [math]4.4.2.4)[/math] Увеличивается [math]i [/math]. Одно сложение.
     Таким образом, т.к. внутренний цикл повторяется [math]   j-1 [/math] раз, а [math]   j [/math] в свою очередь пробегает от [math]1 \dots k [/math], значит, полное количество операций в пункте [math]4.4)[/math], которое будет занимать весь внутренний цикл будет: сравнений [math] \frac{(k-1)k(k+1)}{3} + \frac{k(k-1)}{2} [/math], умножений: [math] 2\frac{k(k-1)}{2}  + \frac{(k-1)k(k+1)}{3} + \frac{(2n)k(k-1)}{2} [/math], сложений [math]\frac{(k-1)k(k+1)}{3} + \frac{(n+1)k(k-1)}{2}[/math] и вычитаний [math] \frac{(n)k(k-1)}{2}[/math]
   [math]4.5)[/math] Ищется норма вектора: [math] n [/math] сложений и умножений
   [math]4.6)[/math] Ищется вектор Ланцоша [math] n [/math] делений
   [math]4.7)[/math] Увеличивается [math] j [/math], одно сложение. 
   
   Так, пункты  [math]4.1 - 4.3, 4.5 - 4.7[/math] занимают [math] k*(n+n+n+1)[/math] сложений, [math]k(n+n+2n+n)[/math] умножений, [math]2nk[/math] вычитаний и [math]n[/math] делений.



Подводя итог, общее количество операций умножения и деления [math]n + n + 2\frac{k(k-1)}{2}  + \frac{(k-1)k(k+1)}{3} + \frac{(2n)k(k-1)}{2} +  k(n+n+2n+n) + n[/math], т.е. [math]O( k^3+nk^2+k^2+kn+n )[/math]
общее количество сложений и вычитаний: [math] n + \frac{(k-1)k(k+1)}{3} + \frac{(n+1)k(k-1)}{2}+ \frac{(n)k(k-1)}{2} + k*(n+n+n+1) + 2nk[/math], т.е.  [math]O( k^3+nk^2+kn+n )[/math]
И [math] \frac{(k-1)k(k+1)}{3} + \frac{k(k-1)}{2} [/math] сравнений ( [math]O( k^3+k^2)[/math]).

рис. 1: Информационный граф

1.7 Информационный граф

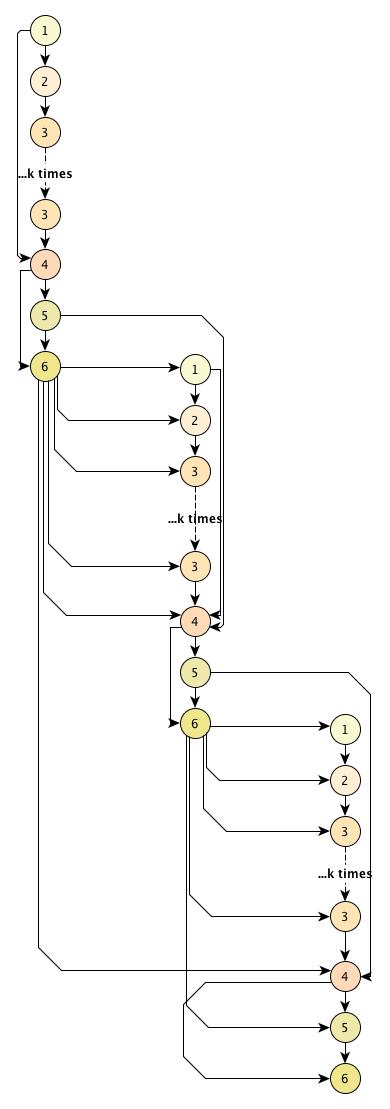
На рисунке (рис. 1) изображен информационный граф. Ниже приведено его описание:

Вершины 1 соответствуют операции [math]Aq_j,[/math].
Вершины 2 соответствуют операции скалярного произведения [math]q_j^Tz[/math].
Вершины 3 соответствуют операции [math]z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i[/math].
Вершины 4 соответствуют операции [math]z-\alpha_jq_j-\beta_{j-1}q_{j-1}[/math].
Вершины 5 соответствуют операции [math]||z||[/math].
Вершины 6 соответствуют операции [math]z/\beta_j[/math].

1.8 Ресурс параллелизма алгоритма

Хотя алгоритм является итерационным, возможно распараллелить внутри каждой итерации умножение матрицы на вектор и процесс переортогонализации Грамма-Шмидта.

Процесс умножения матриц matvec можно распараллелить несколькими способами[1].

Как видно из графа, для выполнения j-й операции, необходимо выполнить следующие ярусы:

[math]n[/math] ярусов сложений с [math]n[/math] операциями умножения в каждом (вычисление [math]z[/math]);
[math]n[/math] ярусов сложений с [math]1[/math] операцией умножения в каждом (вычисление [math]\alpha_j[/math]);
[math]j[/math] ярусов сложений с [math]n[/math] операциями умножения в каждом, [math]n[/math] ярусов сложений с [math]j[/math] операциями умножения в каждом, [math]1[/math] ярус вычитаний размера [math]n[/math] (первая переортогонализация);
[math]j[/math] ярусов сложений с [math]n[/math] операциями умножения в каждом, [math]n[/math] ярусов сложений с [math]j[/math] операциями умножения в каждом, [math]1[/math] ярус вычитаний размера [math]n[/math] (вторая переортогонализация);
[math]n[/math] ярусов сложений с [math]1[/math] операцией умножения в каждом (вычисление [math]\beta_j[/math]);
[math]1[/math] ярус делений размера [math]n[/math] (вычисление [math]q_{j + 1}[/math]).

Если учесть весь ресурс параллелизма, можно получить мультипликативную вычислительную сложность всего алгоритма: [math]O(n^2k+nk^2)/p)[/math].

Вычислительная мощность данного алгоритма, как отношение числа операций к суммарному объему входных и выходных, данных равняется [math]O(k)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные

Матрица [math] A [/math], начальный вектор [math] b [/math] и число собственных значений, которые мы хотим найти [math] k [/math].

Ввиду симметричности из матрицы [math] A [/math] достаточно хранить только ее диагональ и элементы, лежащие выше ее. Таким образом, объем входных данных:

[math]\frac{n (n + 1)}{2} + n + 1 = \frac{n^2+3n+2}{2}.[/math]

Выходные данные

Матрица собственных значений [math] \Lambda = diag(\theta_1 \dots \theta_k) [/math], матрица собственных векторов [math] V = [v_1 \dots v_k] [/math] размера [math] n \times k [/math]

Так, объем выходных данных: [math] k + kn [/math]

1.10 Свойства алгоритма

Если [math]A[/math] эрмитова матрица, то алгоритм Ланцоша и Bi-Lanczos сходятся к одинаковым трехдиагональным матрицам Ритца[2].

При реализации классического алгоритма Ланцоша возникает большая погрешность при округлении. Вариант с полной переортогонализацией позволяет избегать больших погрешностей, однако является более ресурсоемким. Вариант с частичной переортогонализацией является промежуточным.

Алгоритм может завершить свою работу досрочно, когда найденные собственные значения будут достаточно близки к целевым.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

Исследование масштабируемости реализации алгоритма проводилось с использованием стандарта MPI на суперкомпьютере "Ломоносов".

Набор изменяемых параметров запуска реализации алгоритма и границы значений параметров алгоритма:

Число процессоров 4, 8, 16, 32, 64, 128.
Размерность матрицы от 1000 до 50000

Сборка осуществлялась с параметрами:

openmpi/1.5.5-icc
intel/13.1.0

Используемая параллельная реализация алгоритма на языке C++

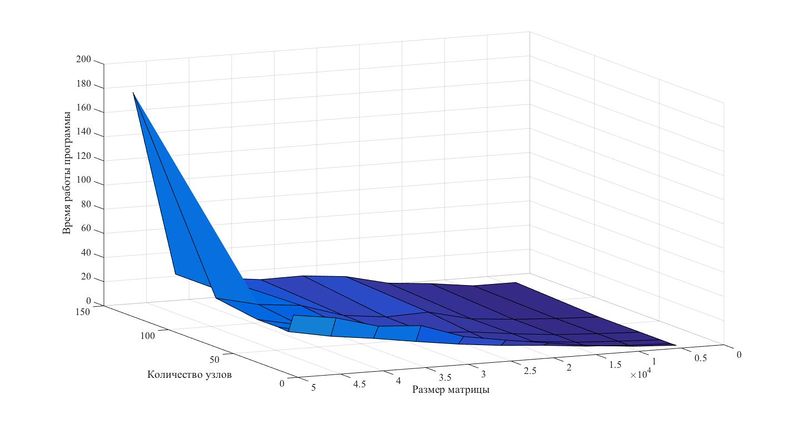
На данном графике отчетливо видно, что время выполнения алгоритма сильно уменьшается с увеличением количества процессов при расчете матрицы любой размерности. При этом наблюдается некоторое снижение производительности в случае наибольших размеров матриц. Данный факт является следствием большого количества данных, необходимого для обмена между процессами. Отсюда опытным путем можно установить, что наибольшая производительность алгоритма будет достигнута, если размерность матрицы не будет превышать 30000-35000.

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Алгоритм Ланцоша реализован в различных пакетах, библиотеках и проектах

NAG Library http://www.nag.com/content/nag-library C, C++, Fortran, C#, MATLAB, R

ARPACK https://people.sc.fsu.edu/~jburkardt/m_src/arpack/arpack.html MATLAB

GrapLab https://turi.com/products/create/open_source.html C++

Gaussian Belief Propagation Matlab Package http://www.cs.cmu.edu/~bickson/gabp/ MATLAB

The IETL Project http://www.comp-phys.org/software/ietl/ C++

LANSO/PLANSO http://web.cs.ucdavis.edu/~bai/ET/lanczos_methods/overview_PLANSO.html Fortran

Julia Math https://github.com/JuliaMath/IterativeSolvers.jl Julia

3 Литература

↑ "The Lanczos Algorithm With Partial Reorthogonalization", Horst D. Simon, Mathematics of computation, volume 42, number 165, pages 115-142 (1984)
↑ Дж. Деммель «Вычислительная линейная алгебра», c. 232, алгоритм 5.2

[1] "The Lanczos Algorithm With Partial Reorthogonalization", Horst D. Simon, Mathematics of computation, volume 42, number 165, pages 115-142 (1984)

[2] Дж. Деммель «Вычислительная линейная алгебра», c. 232, алгоритм 5.2

[1]

[2]