Участник:Allocator/Метод рекурсивной координатной бисекции

Авторы: Долгов Борис (624), Галуза Дмитрий (624)

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Декомпозиция графа — это разбиение множества вершин графа на подмножества, для обработки каждого из подмножеств на отдельном вычислительном узле. Декомпозиция больших графов (то есть графов, объём описания которых превышает память, доступную одному узлу) происходит в два этапа: выполнение первоначального разбиения вершин графа по вычислительным процессорам, затем — выполнение одного из параллельных алгоритмов декомпозиции. Алгоритм координатной рекурсивной бисекции даёт хорошее первичное распределение узлов сетки по сравнению с простым распределением узлов по номерам и, как правило, используется как первый шаг более сложных алгоритмов .

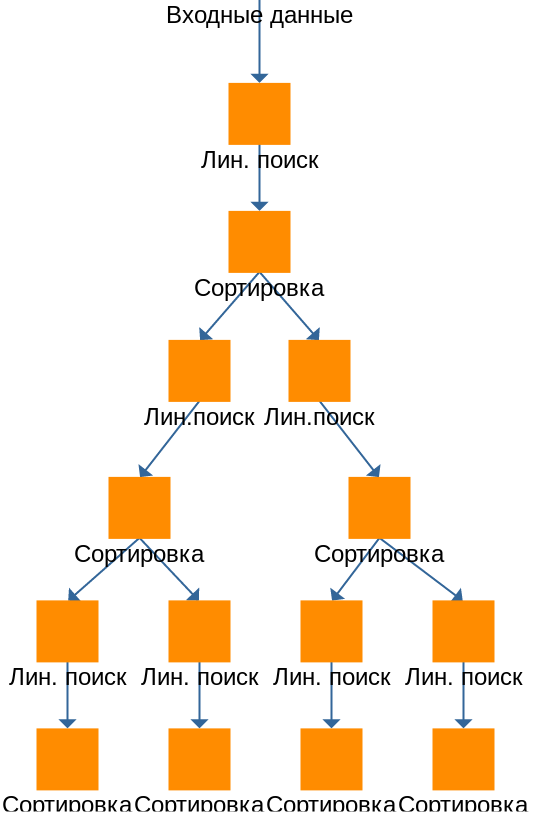
Данный алгоритм использует стратегию рекурсивной бисекции. В соответствии с ней, граф последовательно за k-1 шаг делится на k частей. На первом шаге исходный граф делится на 2 части, на каждом следующем шаге – одна из ранее полученных частей делится ещё на две части. В качестве способа деления на две части используется разделение по координатам вершин. Для этого вершины сортируется вдоль выбранной координаты, и в отсортированном массиве разбиваются на две непрерывные части в заданной пропорции.

Так как алгоритм использует предположение о том, что близкие по координатам вершины будут связаны, а удалённые по координатам вершины будут не связаны, он не подходит для разбивания произвольных графов, а лучше всего подходит для разбития координатных сеток.

1.2 Математическое описание алгоритма

Пусть задан [math]G = (V, E)[/math] – неориентированный граф, где [math]V[/math] -- множество вершин, [math]E[/math] -- множество рёбер. Каждой вершине соответствует целочисленный координатный вектор [math]c_i[/math], вес [math]v_i[/math]. Кроме того, задано желаемое количество доменов [math]p[/math]. Требуется разбить множество [math]V[/math] на p непересекающихся подмножеств (доменов) [math]S_1, \ldots, S_p[/math], при этом должны быть выполнены следующие требования: Домены не пересекаются: [math]S_i \cap S_j = \emptyset[/math] Каждая вершина находится в домене: [math] \cup _i S_i = V[/math] Распределение вершин по доменам примерно равномерное: [math]|S_i| \approx |V| / p[/math] Минимизирован вес разрезанных рёбер: [math]\sum_{i \neq j} \sum_{v_1 \in S_i} \sum_{v2_ \in S_j} e_{v_1, v_2} \rightarrow min[/math] Один шаг алгоритма принимает соотношение для разбиения выглядит следующим образом:

• Выполняется поиск координатной оси, имеющей максимальную протяженность. Под протяженностью понимается разность между максимальным и минимальным значением по выбранной координатной оси серди всех вершин. Сам же поиск максимума и минимума по каждой координатной оси осуществляется одним линейным проходом по вершинам. Для выбора среди разностей – производится еще один линейный проход, уже по координатным осям.
• Вершины сортируются по выбранной координатной оси. Считаем, что одна вершина “меньше” другой, если значение выбранной на предыдущем шаге координаты меньше соответствующего значения другой вершины.
• Полученные на предыдущем пункте отсортированные вершины разбиваются на два домена, согласно заданному соотношению.
• Шаг запускается рекурсивно для полученных доменов.

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма является сортировка на очередном шаге алгоритма, которая при использовании оптимального алгоритма выполняется со сложностью [math]O(n log_2{n})[/math].

1.4 Макроструктура алгоритма

Схема работы параллельного алгоритма следующая:

• Каждый узел находит минимальную и максимальную координату в каждом из измерений на своих данных
• Узлы находят глобальную минимальную и максимальную координату в каждом из измерений, на основании чего принимают решение о максимально протяжённой координате
• Используется любой из параллельных алгоритмов сортировки, в качестве ключа сортировки используется самая протяжённая координата
• После сортировки, начальные K вершин относятся к первому домену, остальные -- ко второму (K выбирается исходя из общего количества вершин и требуемой пропорции деления)
• При необходимости, каждый из кластеров может быть разделён на подкластеры рекурсивным вызовом этого же алгоритма

1.5 Схема реализации последовательного алгоритма

# Шаг алгоритма, принимающий решение о разделении вершин.
# Разбивает граф, передаваемый в переменной graf и имеющий n вершин, на два подграфа
# subgraf1 и subgraf2, имеющих n1 и n2 вершин соответственно.
Bisect(graf, n, subgraf1, n1, subgraf2, n2) {
  # Найти самую протяжённую координату, то есть такое i, для которого разница
  # между максимальным и минимальным значением данной координаты по всем вершинам наибольшая.
  dim = argmax(i, max(j, graf[j][i]) - min(j, graf[j][i]));
  # Отсортировать вершины, используя в качестве ключа значение этой координаты
  sort(graf, dim);
  # Разбить граф на два домена, при этом первые n1 вершин попадут в первый домен, оставшиеся -- во второй.
  subgraf1 = graf[0..n1-1];
  subgraf2 = graf[n1..n-1];
}

# Схема рекурсивной бисекции -- общая часть всех алгоритмов рекурсивной бисекции
# Разбивает граф, передаваемый в аргументе graf и имеющий n вершин
# на k примерно равных доменов, возвращаемых в переменной domains.
RecursiveBisect(graf, n, k, domains) {
  # Найти количество конечных доменов, присутствующих в первой и второй части разбиения на текущем шаге.
  k1 = (k+1)/2;
  k2 = k-k1;
  # Найти количество вершин в первой и второй части разбиения.
  n1=n*k1/k;
  n2=n-n1;
  # Выполнить разбиение на две части в соответствии с алгоритмом координатной бисекции.
  Bisect(graf, n, subgraf1, n1, subgraf2, n2);
  # В случае, если в части присутствует больше одного конечного домена, рекурсивно повторить алгоритм.
  # В противном случае, найденный домен будет входить в ответ данного алгоритма.
  If (k1>1) RecursiveBisect(subgraf1, n1, k1); else domains += subgraf1;
  If (k2>1) RecursiveBisect(subgraf2, n2, k2); else domains += subgraf2;
}

1.6 Последовательная сложность алгоритма

Как было описано ранее, для разбиения графа размером n на p кластеров потребуется p рекурсивных шагов. Таким образом, при использовании оптимальной стратегии разбиения, время работы можно выразить рекуррентным соотношением [math]T(N) = O(N*log_2(N)) + 2 * T(N/2)[/math]. Согласно основной теореме о рекуррентных соотношениях , [math]T(N) = O(N*log_2(N)*log_2(N))[/math] в худшем случае (при N = P). При меньшем количестве кластеров, глубина рекурсии будет ограничена [math]log_2(P)[/math], следовательно, время работы алгоритма составит [math]O(log_2(p) * N * log_2(N))[/math]

1.7 Информационный граф

Шаг алгоритма заключается в разделении входного множества вершин на два домена. Получается, что граф исполнения шагов представляет из себя бинарное дерево. Каждый шаг инициирует исполнение еще двух шагов.

При этом на каждом шаге выполняются действия, описанные в п 1.2.

1.8 Ресурс параллелизма алгоритма

Так как алгоритм работает с координатной сеткой – он обладает координатным параллелизмом. Ярусно-параллельная форма алгоритма имеет высоту в [math]log_2 k[/math] уровней, где k – требуемое значение конечных доменов. Соответственно ширина яруса i будет равна [math]2^i[/math]. Так как ширина i-го яруса равна [math]2^i[/math], а общее количество вершин примем за n – то в кажом домене на i-м ярусе будет по [math]n / 2^i[/math] вершин. Если на каждом шаге использовать параллельную сортировку c хорошей сложностью [math](n/p)(log_2(n/p)+log_2^2(p))[/math] (где n - количество сортируемых элементов, p - количество процессоров), то получаем итоговую сложность алгоритма как сумму всех ярусов, на которых параллельно запускается сортировка. А именно: [math]\sum_{i=0}^{log_2 k} ((n / 2^i) / (p / 2^i)) (log_2((n / 2^i) / (p / 2^i)) + log_2^2(p / 2^i)) = O((n/p) * (log_2 (n/p) + log_2^2(p)) * log_2(k))[/math]

1.9 Входные и выходные данные алгоритма

Входные данные: требуемое количество доменов в разбиении, вершины графа. Каждой вершине соответствуют некоторые многомерные числовые координаты. Вершины могут быть произвольно разбиты по вычислительным узлам. Таким образом, объём входных данных пропорционален размеру графа V и количеству измерений N: [math]|V|*N+|E|[/math].

Выходные данные: p доменов, разбивающих граф; при этом вершины этих доменов хранятся последовательно в исходном массиве. При количестве узлов, используемых для декомпозиции, совпадающим с количеством узлов, используемых для дальнейших вычислений, это автоматически размещает всю информацию о вершинах на вычислительных узлах, которые будут обрабатывать эти вершины. Таким образом, объём выходных данных пропорционален количеству вершин в исходном графе: |V|.

1.10 Свойства алгоритма

Приведенный алгоритм является устойчивым по построению, так как отсутствуют операции, которые могут нарушить устойчивость (например, вычисления с вещественными числами с плавающей точкой). Работа ведется с целочисленными координатами, что приводит к исключению ошибок округления и прочих побочным эффектам.

Детерминированность данного алгоритма может быть достигнута, если использовать устойчивый алгоритм сортировки.

Так как процессы обрабатывают примерно равное количество вершин, полученный алгоритм является сбалансированным по числу операций на каждом процессе.

Вычислительная мощность алгоритма, равная отношению количества операций к количеству входных и выходных данных равна [math]((|V|/P) * (log_2 (|V|/P) + log_2^2(P)) * log_2(K) / (|V|N+|E|) = [/math]. Если принять количество вычислительных узлов P и количество измерений N за константы, а количество ребёр пропорциональным количеству вершин (что верно для координатных сеток), вычислительная мощность будет равна [math]O(log_2(|V|) * log_2(K))[/math]

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

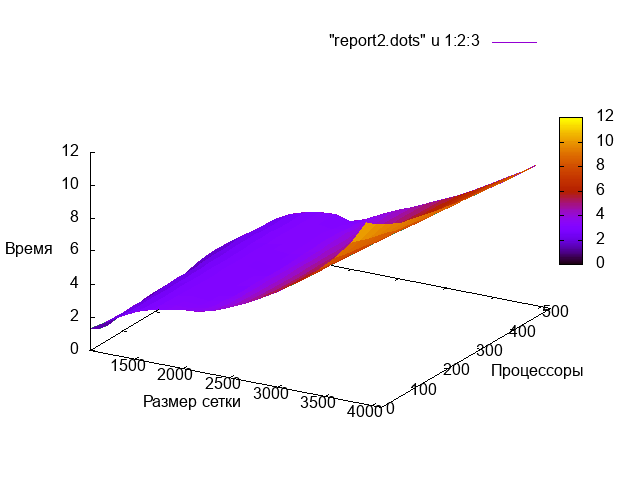
Оценка масштабируемости метода рекурсивной координатной бисекции проводилась на основе существующей реализации. Из существующих реализаций была выбрана наиболее широко используемая на данный момент реализация из программной библиотеки для распределения нагрузки Zoltan.

Входными данными были двумерные регулярные сетки, которые генерировались непосредственно внутри самой программы. Исходная реализация предполагала чтение с файла, но в данном случае накладные расходы на чтение оказываются неоправданны.

Запуск производился на суперкомпьютере ВМК МГУ BlueGene/P и осуществлялся следующей программой на языке BASH

#!/bin/bash
for size in 1024 2048 4096; do
  for procs in 1 2 16 64 128 256 512; do
    mpisubmit.bg -n $procs -w 3:00 -m smp --stdin /dev/null --stderr ~/output2/$size-$procs.log --stdout /dev/null ./simpleRCB.exe -- $size
  done
done

Результаты запуска при разбиении на 16 доменов показаны ниже.

2.7 Существующие реализации алгоритма

Открытые параллельные и последовательные реализации существуют в пакете алгоритмов декомпозиции METIS и ParMETIS: http://glaros.dtc.umn.edu/gkhome/software

Кроме того, он пристутсвует в библиотеках Zoltan (https://www.cs.sandia.gov/zoltan/), Scotch и PT-Scotch (https://www.labri.fr/perso/pelegrin/scotch/).