Участник:Павел/Алгоритм кластеризации категорийных данных CLOPE

Материал из Алговики
Перейти к навигации Перейти к поиску

Автор описания: П.М.Бронников

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Алгоритм CLOPE (Clustering with sLOPE[1]) неирархический метод кластеризации, предназначенный для кластеризации огромных наборов категорийных данных. К достоинствам алгоритма относятся высокие масштабируемость и скорость работы и качество кластеризации, что достигается использованием глобального критерия оптимизации на основе максимизации градиента высоты гистограммы кластера. Отличается простотой программной реализации.

Во время работы алгоритм хранит в памяти небольшое количество информации по каждому кластеру и требует минимальное число сканирований набора данных. CLOPE автоматически подбирает количество кластеров, причем это регулируется одним единственным параметром - коэффициентом отталкивания [math] r [/math]. При этом он обеспечивает более высокую производительность и лучшее качество кластеризации в сравнении с многими иерархическими алгоритмами.

1.2 Математическое описание алгоритма

Пусть имеется база транзакций [math]D[/math], состоящая из множества транзакций [math]\{t_1,t_2,...,t_n\}[/math]. Каждая транзакция есть набор объектов [math]\{i_1,...,i_m\}[/math]. Множество кластеров [math]\{C_1,...,C_k\}[/math] есть разбиение множества [math]\{t_1,...,t_n\}[/math], такое, что [math]C_1 \cup \dots \cup C_k=\{t_1,...,t_n\}[/math] и [math]C_i \ne \empty[/math] и [math]C_i \cap C_j = \empty [/math], для [math]i \ge 1, k \ge j[/math]. Каждый элемент [math]C_i[/math] называется кластером, а [math]n, m, k[/math] – количество транзакций, количество объектов в базе транзакций и число кластеров соответственно.

Каждый кластер [math]C[/math] имеет следующие характеристики: [math]D(C)[/math] – множество уникальных объектов;

[math]Occ(i,C)[/math] – количество вхождений (частота) объекта [math]i[/math] в кластер [math]C[/math];

[math]S(C)= \sum_{i \in D(C)} Occ(i,C)= \sum_{t_i \in C} \mid t_i \mid , [/math]

[math]W(C)= \mid D(C) \mid ,H(C)=S(C)/W(C) [/math]

Функция стоимости:

[math] Profit(C) = \frac{\sum^{k}_{i=1} G(C_i) \times \mid C_i \mid} {\sum^{k}_{i=1} \mid C_i \mid } = \frac{\sum^{k}_{i=1} \frac{S(C_i)}{W(C_i)^r} \times \mid C_i \mid} {\sum^{k}_{i=1} \mid C_i \mid } [/math]

где [math]\mid C_i \mid[/math] количество объектов в [math]i[/math]-ом кластере, [math]k[/math] – количество кластеров, [math]r[/math] – коэффициент отталкивания [math](0 \lt r \le 1)[/math]

С помощью параметра [math]r[/math] регулируется уровень сходства транзакций внутри кластера, и, как следствие, финальное количество кластеров. Этот коэффициент подбирается пользователем. Чем больше [math]r[/math], тем ниже уровень сходства и тем больше кластеров будет сгенерировано.

Постановка задачи кластеризации алгоритмом CLOPE выглядит следующим образом:

для заданных [math]D[/math] и [math]r[/math] найти разбиение [math]C[/math] такое, что: [math]Profit(C) \longrightarrow max [/math] [2].

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма состоит в вычислении на каждой итерации стоимости добавления и удаления транзакции из кластера:

  • вычисление нового размера кластера [math]S_{new}(C_i)=S(C_i) \pm \mid(t_n)\mid [/math], где [math]\mid(t_n)\mid[/math] - длина транзакции
  • вычисление новой ширины кластера [math]W_{new}(C_i)=\mid D(C_i \cup t_n)|[/math]
  • вычисление стоимости [math]\frac{S_{new}(C_i)(\mid C_i \mid \pm 1)}{W_{new}(C_i)^r} - \frac{S(C_i) \mid C_i \mid }{W(C_i)^r}[/math]

1.4 Макроструктура алгоритма

Алгоритм состоит из следующих этапов:

1. Инициализация. На этом этапе происходит первый проход по таблице с транзакциями для построения начального разбиения, для каждой транзакции определяется кластер исходя из максимизации стоимости.

2. Итерация. На данном этапе для каждой транзакции проводится попытка перемещения в другой кластер для максимизации функции стоимости.

1.5 Схема реализации последовательного алгоритма

InitIter.PNG

Первая часть алгоритма - инициализация: для каждой транзакции вычисляется кластер, к которому она будет отнесена исходя из максимизации функции стоимости. Для этого вычисляется вспомогательная функция DeltaAdd, которая считает стоимость добавления транзакции к одному из существующих кластеров, либо к пустому. В итоге транзакция помещается в кластер, для которого цена добавления максимальна.

Вторая часть алгоритма - уточняющие итерации: здесь происходит попытка улучшить вычисленные на первом этапе кластеры. В каждой итерации происходит перебор всех транзакций, и для каждой транзакции вычисляется цена удаления ее из текущего кластера и цена добавления в другой кластер. Суммарная стоимость перемещения будет являться суммой стоимостей удаления и добавления. Если максимальная стоимость перемещения данной транзакции в какой-либо больше нуля, то она перемещается в этот кластер.

Вычисления происходят до тех пор, пока за итерацию происходит хотя бы одно перемещение транзакции. Если за итерацию не было произведено ни одного перемещения, то текущее состояние кластеров является устойчивым и оптимальным. [3]

Схема реализации на псевдокоде:

Входные параметры:

  • [math]t[/math] - транзакции
  • [math]r[/math] - коэффициент отталкивания

Выходной параметр:

  • [math]C[/math] кластеры, в начале алгоритма - пустое множество

Инициализация: 

   for t_i in t:
   max = 0
       for C_j in C:
           if DeltaAdd(C_j,t_i,r) > max:
               max = DeltaAdd(C_j,t_i,r)
               C_best = C_j
   put t_i in C_best

Итерации: 

   move = True
   while move == True:
   move = False
       for t_i in t:
           max = 0
           C_now = t_i.cluster
           removeCost = DeltaRemove(C_now,t_i,r)
           for C_j in C:
               if DeltaAdd(C_j,t_i,r) + removeCost > max:
                   max = DeltaAdd(C_j,t_i,r) + removeCost
                   C_best = C_j
       if max > 0
           del t_i from C_now
           put t_i in C_best
           move = True

Вспомогательная функция DeltaAdd: 

   function DeltaAdd(C,t,r)
       S_new=C.size + t.itemCount
       W_new=C.wigth
       for item in t_i:
           if C_j.occ(item) = 0
               W_new = W_new + 1
       return S_new * (C.count+1) / (W_new ^ r) - (C.size * C.count) / (C.wigth ^ r)

Вспомогательная функция DeltaRemove: 

   function DeltaRemove(C,t,r)
       S_new=C.size - t.itemCount
       W_new=C.wigth
       for item in t:
           if C_j.occ(item) = 1
               W_new = W_new - 1
       return S_new * (C.count-1) / (W_new ^ r) - (C.size * C.count) / (C.wigth ^ r)

1.6 Последовательная сложность алгоритма

В соответствии с ранее введенным обозначением [math]n[/math] - количество транзакций, [math]m[/math] - длина транзакции(максимальная), [math]k[/math] - количество кластеров.

Основные вычисления восполняются в функции DeltaAdd/DeltaRemove: производится 1 сложение, не более [math]m[/math] сложений/вычитаний, 2 умножения, 2 деления, 2 возведения в степень и 1 сложение - итого [math]m + 8[/math] операций.

Операции выполняются для всех транзакций ([math]n[/math] штук) и для всех кластеров ([math]k[/math] штук). Итого выполняется [math]n*k*(m+8)[/math] операций.

В добавок к этому при добавлении/удалении транзакции к кластеру производится пересчет его характеристик: [math]m+2[/math] операции.

Из того можно сделать вывод, что оценка сложность алгоритма равна [math]O(n*k*m)[/math].

1.7 Информационный граф

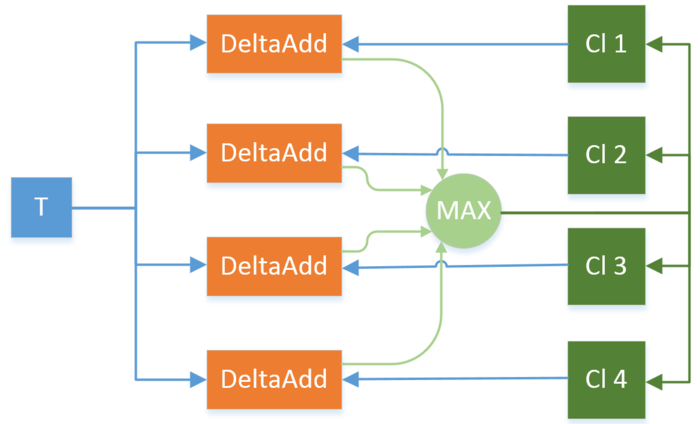
На рисунке ниже представлена схема этапа инициализации на примере входной транзакции T и четырех кластеров Cl 1, Cl 2, Cl 3 и Cl 4.

Объект DeltaAdd соответствует выполнению соответствующей функции для вычисления цены добавления транзакции на кластер. После выполнения всех DeltaAdd для одной транзакции выполняется определение максимального значения функции и выбор кластера, на который будет помещена транзакция. На этапе инициализации при обработке каждой транзакции количество кластеров может как увеличиться, так и остаться неизменным.

InitDef.PNG

Этап итераций отличается только тем, что на нем дополнительно считается функция DeltaRemove вычисления стоимости удаления транзакции с кластера. На этапе итерации функции DeltaAdd/DeltaRemove могут считать параллельно для каждой транзакции.

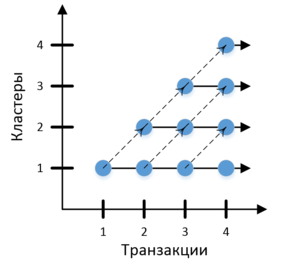
Синие точки сетки - вычисление функций DeltaAdd. На этапе инициализации количество кластеров может как увеличиться, так и не измениться, это показано пунктирными линиями.

Этап Инициализации

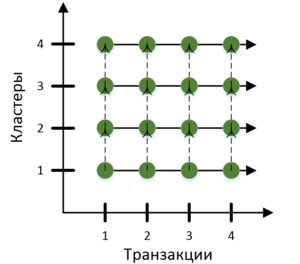
Зеленые точки сетки - вычисление функций DeltaAdd и DeltaRemove. На этапе итераций функции могут считаться параллельно для каждой транзакции.

Этап Итераций

1.8 Ресурс параллелизма алгоритма

Вычисление стоимости добавления/удаления транзакции, которые выполняются функциями DeltaAdd/DeltaRemove, происходит независимо для всех [math]k[/math] кластеров. Поэтому все вычисления можно производить параллельно. Таким образом сложность алгоритма с [math]O(n*k*m)[/math] понижается до [math]O(n*m)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные:

[math]n[/math] транзакций длины [math]m[/math] и коэффициент отталкивания [math]r[/math]

Выходные данные:

метки классов для каждой транзакции в соответствии с проведенной кластеризацией(числовая последовательность длины [math]n[/math])

1.10 Свойства алгоритма

  • Соотношение последовательной и параллельной сложности алгоритма определяется количеством кластеров: [math]\dfrac{O(n*k*m)}{O(n*m)} = k[/math]
  • Вычислительная мощность алгоритма равна [math]\dfrac{nk(m+8) + m + 2}{nm + n + 1} \cong k[/math]
  • Алгоритм не является устойчивым, так как результат работы зависит от порядка чтения транзакций и от текущего набора транзакций в кластере.
  • Выполняется свойство сбалансированности операций между параллельными ветвями алгоритма, так как для каждой транзакции выполняются функции DeltaAdd/DeltaRemove, считающие стоимость добавления/удаления транзакции.
  • Свойство детерминированности алгоритмов не выполняется, так как результат алгоритма зависит от порядка прохождения транзакций. Но если рассматривать транзакции как нумерованный список, то результат будет определен однозначно от запуска к запуску. Однако существует расширение алгоритма, обеспечивающее свойство детерминированности. [4].
  • Так как алгоритм предназначен для кластеризации категориальных данных, то он практически неприменим для числовой кластеризации.
  • Быстро работает даже для большого количества данных, обеспечивая при этом хорошее качество кластеризации
  • Имеет простую реализацию

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

Проверка масштабируемости проводилась на суперкомпьютере "Ломоносов" с использованием компилятора Intel(13.1.0) и стандарта OpenMP для 1000, 2000, 3000, 4000 и 5000 транзакций из пяти латинских букв с использованием 1, 2, 4, 8 и 16 нитей. Использованные параметры компиляции и запуска: 

   icc -openmp CLOPE.cpp -o clope
   
   export OMP_NUM_THREADS = k (k - число нитей)
   sbatch -p test -N 1 run ./clope tr 5 3 (tr - количество транзакций)

Используемая реализация: 

   #include <cstdio>
   #include <cstdlib>
   #include <cmath>
   #include <cstring>
   #include <set>
   #include <vector>
   #include "omp.h"
   
   using namespace std;
   
   double r = 1.6;
   int t_num = 5000;
   int t_len = 5;
   
   struct Clust
   {
     int size;
     int count;
     int width;
     multiset <char> clus;
     Clust(){
         size = 0;
         count = 0;
         width = 0;}
   };
   
   void AddTransaction(Clust &C, char* t)
   {
     C.size = C.size + t_len;
     C.count = C.count + 1;
   
     for (int i = 0; i < t_len; i++){
       if (C.clus.count(t[i]) == 0) {
         C.width = C.width + 1;
       }
       C.clus.insert(t[i]);
     }
   }
   
   void RemoveTransaction(Clust &C, char* t)
   {
     C.size = C.size - t_len;
     C.count = C.count - 1;
   
     for (int i = 0; i < t_len; i++){
       if (C.clus.count(t[i]) == 1) {
         C.width = C.width - 1;
       }
       C.clus.erase(C.clus.find(t[i]));
     }
   }
   
   double AddCost(Clust C, char* t)
   {
     int S = C.size;
     int N = C.count;
     int W = C.width;
     int Snew = S + t_len;
     int Nnew = N + 1;
     int Wnew = W;
     set <int> tmp;
   
     for (int i = 0; i < t_len; i++){
       if (C.clus.count(t[i]) == 0 && tmp.count(t[i]) == 0) {
         Wnew = Wnew + 1;
       }
       tmp.insert(t[i]);
     }
     return (Snew * Nnew) / (pow(Wnew, r)) - ((S == 0) ? 0 : (S * N) / (pow(W, r)));
   }
   
   double RemoveCost(Clust C, char* t)
   {
     int S = C.size;
     int N = C.count;
     int W = C.width;
     int Snew = S - t_len;
     int Nnew = N - 1;
     int Wnew = W;
   
     for (int i = 0; i < t_len; i++){
       if (C.clus.count(t[i]) == 1) {
         Wnew = Wnew - 1;
       }
     }
     return ((Wnew == 0) ? 0 : (Snew * Nnew) / (pow(Wnew, r))) - (S * N) / (pow(W, r));
   }
   
   int main(int argc, char **argv)
   {
     int ClusCnt = 0;
     double maxCost;
     int bestChoice;
     double remCost;
       int i, j, k;
       int tr = omp_get_max_threads();
       bool moved = false;
   
   t_num = atoi(argv[1]);
   t_len = atoi(argv[2]);
   r = atof(argv[3]);
   
     int* Distr = (int*)malloc(t_num * sizeof(int));
   
     char** T = (char **)malloc(t_num * sizeof(char*));
     T[0] = (char *)malloc(t_num * t_len * sizeof(char));
     for (i=1; i < t_num; i++){
       T[i] = T[i-1] + t_len;
     }
   
       vector<Clust> C;
       C.push_back(Clust());
   
     FILE* input = fopen("input.txt", "r");
         for (i = 0; i < t_num; i++) {
           for (j = 0; j < t_len; j++) {
             fscanf(input, "%c ", &T[i][j]);
           }
         }
   
   //Инициализация
   
     double tm = omp_get_wtime();
     AddTransaction(C[0], T[0]);
     ClusCnt++;
     C.push_back(Clust());
   
       Distr[0] = 0;
   
     for (i = 1; i < t_num; i++){
       maxCost = 0;
       double add[ClusCnt + 1];
   
       #pragma omp parallel for private(j) shared(ClusCnt, add, C, T)
       for (j = 0; j <= ClusCnt; j++){
         add[j] = AddCost(C[j], T[i]);
       }
   
         for (j = 0; j <= ClusCnt; j++){
         if (add[j] > maxCost){
           maxCost = add[j];
           bestChoice = j;
         }
       }
   
   
       if (bestChoice == ClusCnt){
         ClusCnt++;
         C.push_back(Clust());
       }
       AddTransaction(C[bestChoice], T[i]);
       Distr[i] = bestChoice;
     }
   
   //Итерации
     for (k = 0; k < 10; k++){ // k - число итераций
         moved = false;
         double add[ClusCnt + 1];
   
         for (i = 0; i < t_num; i++){
          maxCost = 0;
          remCost = RemoveCost(C[Distr[i]],T[i]);
   
          #pragma omp parallel for private(j) shared(ClusCnt, add, C, T, Distr, remCost)
          for (j = 0; j <= ClusCnt; j++){
           if (j != Distr[i]) {
             add[j] = AddCost(C[j], T[i]) + remCost;
             }
          }
           for (j = 0; j <= ClusCnt; j++){
             if (j != Distr[i]){
             if (add[j] > maxCost) {
               maxCost = add[j];
               bestChoice = j;
               }
             }
           }
   
           if (maxCost > 0){
             if (bestChoice == ClusCnt){
               ClusCnt++;
               C.push_back(Clust());
             }
             RemoveTransaction(C[Distr[i]], T[i]);
             AddTransaction(C[bestChoice], T[i]);
             Distr[i] = bestChoice;
             moved = true;
           }
         }
     }
   
   tm = omp_get_wtime() - tm;
   
   printf("size:%d\twidth:%d\tcl_cnt:%d\threads:%d\ttime:%lf seconds\tr:%lf",t_num,t_len,ClusCnt - 1,tr,tm,r);
   
   
   FILE* output = fopen("out.txt","w");
   for (int j = 0; j <= ClusCnt; j++){
       fprintf(output,"Cluster %d:\n",j);
       for (multiset<char>::iterator it = C[j].clus.begin(); it != C[j].clus.end(); it++){
               fprintf(output,"%c",*it);
       }
       fprintf(output,"\n");
   }
   
   fclose(input);
   fclose(output);
   free(T[0]);
   free(T);
   free(Distr);
   
   return 0;
   }


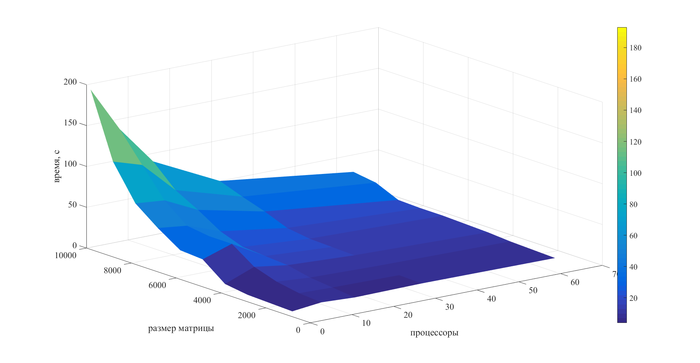
Результаты проверки на графике ниже.

//Graf lom.png

//Таким образом, можно сделать вывод о том, что алгоритм кластеризации CLOPE является масштабируемым.

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Также существуют пользовательские реализации алгоритма:

3 Литература

  1. ↑ Yang, Y., Guan, H., You. J. CLOPE: A fast and Effective Clustering Algorithm for Transactional Data In Proc. of SIGKDD’02, July 23-26, 2002, Edmonton, Alberta, Canada.
  2. ↑ Нейский И.М. Классификация и сравнение методов кластеризации.
  3. ↑ Павлин Н. Кластеризация категорийных данных: масштабируемый алгоритм CLOPE, https://basegroup.ru/community/articles/clope
  4. ↑ Li, Y., Le, J., Wang, M. Improving CLOPE’s Profit Value and Stability with an Optimized Agglomerative Approach. Algorithms 2015, 8, 380-394.
Источник — https://algowiki-project.org/w/ru/index.php?title=Участник:Павел/Алгоритм_кластеризации_категорийных_данных_CLOPE&oldid=22500