Сеть нечетно-четной перестановки
Версия от 23:18, 9 мая 2019; Lira (обсуждение | вклад)
Сеть нечетно-четной перестановки
Содержание
- 1 Описание свойств и структуры алгоритма
- 1.1 Словесное описание алгоритма
- 1.2 Математическое описание
- 1.3 Вычислительное ядро алгоритма
- 1.4 Описание схемы реализации последовательного алгоритма
- 1.5 Последовательная сложность алгоритма
- 1.6 Информационный граф
- 1.7 Описание ресурса параллелизма алгоритма
- 1.8 Описание входных и выходных данных
- 1.9 Свойства алгоритма
- 2 Программная реализация
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Описание локальности данных и вычислений
- 2.3 Возможные способы и особенности реализации параллельного алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Описание свойств и структуры алгоритма
1.1 Словесное описание алгоритма
Сеть сортировки размером [math]n[/math] задаёт расписание для упорядочивания [math]n[/math] элементов массива. Сеть нечетно-четной перестановки является масштабируемой, поскольку может быть построена для любого числа элементов [math]n \ge 3[/math].
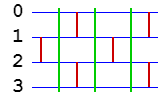
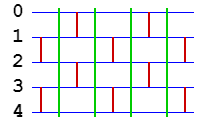
Сеть состоит из [math]n[/math] стадий. На стадиях с чётными номерами выполняются операции сравнения-перестановки пар элементов с номерами [math] 2*i и 2*i+1 [/math], на стадиях с нечётными номерами выполняются операции сравнения-перестановки пар элементов с номерами [math] 2*i-1 и 2*i [/math]. Пример для [math] n = 4, 5 [/math] приведён на рисунках 1 и 2.