Repeated Thomas, locality
Содержание
1 Ссылки
2 Локальность данных и вычислений
Как видно по графу алгоритма, локальность данных по пространству хорошая - все аргументы, которые необходимы для операций, вычисляются "рядом". Однако по времени локальность вычислений не столь хороша. Если данные задачи не помещаются в кэш, то вычисления в "верхнем левом углу" СЛАУ будут выполняться с постоянными промахами кэша. Отсюда может следовать одна из рекомендаций прикладникам, использующим прогонку, - нужно организовать все вычисления так, чтобы прогонки были "достаточно коротки" для помещения данных в кэш.
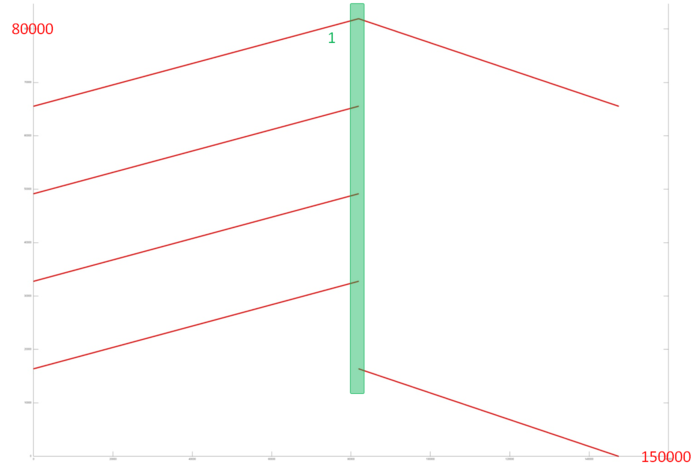
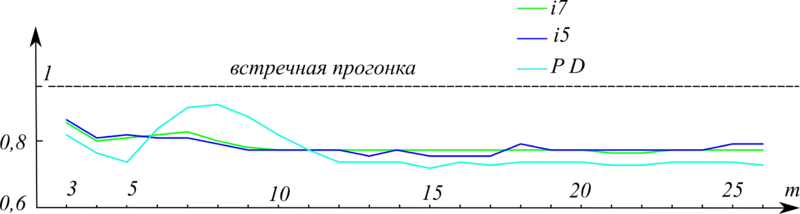
При этом, однако, повторная прогонка относится к таким последовательным алгоритмам, в которых локальность вычислений настолько велика, что является даже излишней[1]. Из-за того, что данные, необходимые для выполнения основных операций прогонки, вычисляются в непосредственно предшествующим им операциях, возможность использования суперскалярности вычислительных ядер процессоров практически сводится на нет, что ухудшает эффективность выполнения прогонки даже на современных однопроцессорных и одноядерных системах. Последнее показано сравнением времени исполнения монотонной повторной прогонки и встречной монотонной прогонки[2], которая благодаря наличию двух ветвей вычислений даёт выигрыш по времени около 20% в сравнении с первой даже на персональных компьютерах (см. Рисунок 1).
2.1 Локальность реализации алгоритма
2.1.1 Структура обращений в память и качественная оценка локальности
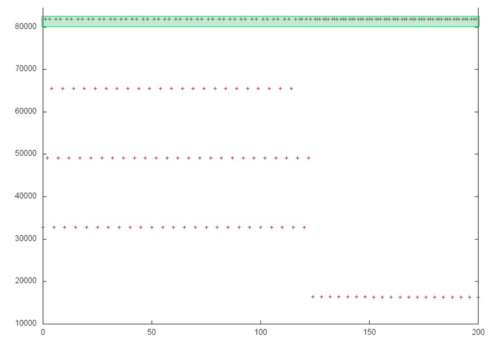
На рис. 2 представлен общий профиль обращений в память для реализации повторного варианта классической монотонной прогонки. Явно видно два этапа в работе программы – на первом этапе выполняется перебор 4 массивов в прямой последовательности, а на втором этапе 2 массива перебираются в обратной последовательности. Профиль состоит из фрагментов, каждый из которых очень похож на обычный последовательный перебор, который обладает высокой пространственной и низкой временной локальностями. Однако необходимо более детальное рассмотрение профиля, чтобы понять, как именно этот перебор устроен.
На рис. 3 представлен фрагмент 1 (выделен на рис. 2 зеленым). В данном фрагменте происходит смена двух этапов, а также входят обращения ко всем массивам. Из рис. 3 видно, что перебор 4 массивов в нижней части рисунка состоит из единичных обращений; в данном случае фрагменты представляют собой обычный последовательный перебор элементов массива, возможно с некоторым небольшим шагом по памяти. Однако самая верхняя часть фрагмента отличается от остальных, более того, можно увидеть, что характер обращений на разных этапах отличается. Рассмотрим данную часть более детально.
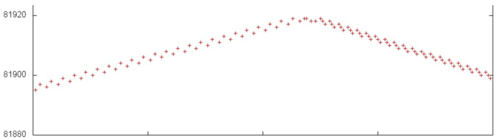
На рис. 4 представлена часть фрагмента 1, выделенная зеленым на рис. 3. Можно увидеть, что, действительно, профили на разных этапах отличаются. На первом этапе выполняются два параллельно последовательных перебора, при этом сдвиг по памяти между ними очень невелик. На втором этапе параллельно выполняется уже три последовательных перебора, причем сдвиг по памяти также очень мал. При таких условиях пространственная локальность высока, поскольку данные перебираются почти последовательно. Временная локальность для данной части относительно невысока, поскольку повторных обращений к данным немного, хотя они расположены очень близко друг к другу.
Отметим, однако, что, во-первых, переборы других массивов реже используют данные повторно, и, во-вторых, данные также повторно используются на разных этапах далеко друг от друга, что приводит к достаточно серьезному снижению временной локальности при рассмотрении общего профиля.
В целом можно сказать, что общий профиль обладает высокой пространственной и достаточно низкой временной локальностью.
2.1.2 Количественная оценка локальности
Оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
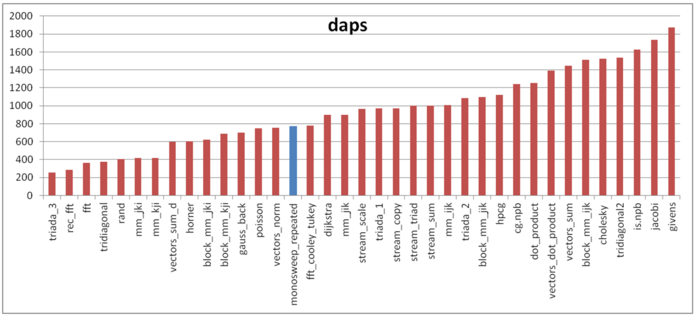
На рисунке 5 приведены значения daps для реализаций некоторых распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что производительность работы с памятью в данном случае достаточно невысока и находится на уровне таких алгоритмов, как вычисление нормы вектора и решение уравнения Пуассона. По всей видимости, это связано с достаточно низкой временной локальностью, как было сказано выше.
Однако отметим, что в целом данный профиль обладает более высокой производительностью работы с памятью по сравнению с большинством алгоритмов, которые представляют собой совокупность различных последовательных переборов, таких как вычисление нормы вектора, реализация схемы Горнера и т.д.
3 Масштабируемость алгоритма и его реализации
О масштабируемости самой прогонки, как полностью непараллельного алгоритма, говорить не имеет смысла. Однако необходимо отметить, что анализ масштабируемости параллельных вариантов прогонки должен проводиться относительно однопроцессорной реализации описанного классического варианта прогонки, а не относительно однопроцессорных расчетов для её параллельных вариантов.
3.1 Масштабируемость алгоритма
3.2 Масштабируемость реализации алгоритма
4 Динамические характеристики и эффективность реализации алгоритма
В силу существенно последовательной природы алгоритма и его избыточной локальности, исследование его динамических характеристик представляется малоценным.
5 Результаты прогонов
6 Литература =
- ↑ Фролов А.В., Антонов А.С., Воеводин Вл.В., Теплов А.М. Сопоставление разных методов решения одной задачи по методике проекта Algowiki // Параллельные вычислительные технологии (ПаВТ'2016): труды международной научной конференции (г. Архангельск, 28 марта - 1 апреля 2016 г.). Челябинск: Издательский центр ЮУрГУ, 2016. С. 347-360.
- ↑ Фролов Н.А., Фролов А.В. Экспериментальные исследования влияния степени локальности алгоритмов на их быстродействие на примере решения трёхдиагональных СЛАУ // Труды 59й научной конференции МФТИ (21–26 ноября 2016 г., гг. Москва-Долгопрудный).