Участник:Снисаренко Ольга/Алгоритм четно-нечетного слияния Бетчера
Алгоритм четно-нечетного слияния Бетчера
Алгоритм четно-нечетного слияния Бетчера (odd-even mergesort) является вариантом сортировки слиянием, который использует параллельные вычисления для ускорения процесса сортировки. Он был разработан в 1968 году американским информатиком Ричардом Бетчером.
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Алгоритм не слишком популярный и не слишком известный. Однако он достаточно легко параллелится и его реализация не слишком сложна. Он основан на алгоритме слияния, который объединяет две отсортированные половины последовательности в полностью отсортированную последовательность. В отличие от сортировки слиянием, этот алгоритм не зависит от данных, т.е. одни и те же сравнения выполняются независимо от фактических данных. Следовательно, четно-нечетную сортировку слиянием можно реализовать как сортировочную сеть.[1] Вместе с битонной сортировкой является одним из первых методов построения сортировочной сети для любого количества входов. [2]
Время работы алгоритма составляет O(log2(n)) (с использованием параллелизма), как и в алгоритмах битонной сортировки и сортировки Шелла. Однако сортировка слиянием нечетной четности требует наименьшего количества операций сравнения.
1.2 Математическое описание алгоритма
Алгоритмом сортировки называется процесс упорядочиванием элементов в списке. На вход поступает неотсортированный массив чисел. Выходными данными алгоритма является массив, отсортированный в порядке неубывания или невозрастания.
В оставшейся части этого раздела мы будем предполагать, что длина нашего списка n равна степени 2. В случае, если это не так, необходимо добавить фиктивные элементы, однако это не влияет на асимптотическую сложность.
Идея алгоритма Бэтчера заключается в следующем утверждении: если вы разделите последовательность пополам, далее рекурсивно отсортируете первую половину списка, а так же рекурсивно отсортируете вторую половину отедельно, а затем отсортируете записи с нечетным индексом всей последовательности (первая, третья, пятая,...) и записи с четным индексом всей последовательности (второй, четвертый, шестой,...) отдельно, то после повторения операций сравнения между отдельными парами на четных и нечетных позициях элементов, мы получим отсортированный список.
К примеру:
Давайте посмотрим, что происходит с конкретным списком длины 8. Предположим, нам дан следующий список
2 7 6 3 9 4 1 8
Мы хотим отсортировать его от меньшего к большему. Если отсортировать первую и вторую половинки отдельно, получим:
2 3 6 7 1 4 8 9
Сортировка ключей с нечетным индексом (2, 6, 1, 8), а затем ключей с четным индексом (3, 7, 4, 9) при выходе
их в нечетных и четных местах соответственно дает:
1 3 2 4 6 7 8 9
Этот список теперь почти отсортирован: делаем сравнение между элементами в позициях (2 и 3), (4 и 5) и (6 и 7) фактически завершат сортировку.[3]
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма Батчера представлено в: 1. Рекурсивная сортировка первой и второй половин списка, его объединение 2. Сортировка ключей с четным/нечетным индексом по-отдельности 3. Объединение списка во едино и попарное сравнение элементов на соседних позициях
1.4 Макроструктура алгоритма
В программе используется алгоритм генерации случайных чисел, но он не влияет на показатели времени при выполнении сортировки. Алгоритм дает большой выигрыш при использовании его параллельно. Процессы обмениваются элементами своих массивов, чтобы при объединении в один массив образовался в конечном итоге был отсортированный массив.
1.5 Схема реализации последовательного алгоритма
Исходный массив разделяется на две части пополам. Рекурсивно сортируем обе последовательности. После чего, склеиваем обе последовательности обратно в одну. Эту последовательность можно эффективно отсортировать. То есть выбираются элементы, занимающие четные позиции, отправляются в первую половину результирующего массива, нечетные — во вторую. После этого необходимо отсортировать каждую из этих половин, а затем переместить их обратно согласно четности/нечестности позиции. Получается, что отсортированные элементы из нечетной подпоследовательности по возрастанию займут 1, 3, 5, 7 места в нашем массиве, а сортированные элементы с четных позиций займут соответственно места 2, 4, 6 и так далее. После чего останется только сравнить и отсортировать элементы на соседних позициях между собой. Итак, мы получили отсортированный массив. Сложность такой реализации O(nlog2n), поскольку мы использовали сортировку, работающую за O(nlogn), а всего уровней было logn.
1.6 Последовательная сложность алгоритма
Сложность алгоритма четно-нечётного слияния Бэтчера зависит от количества элементов в массиве. Эту величину будем обозначать как n. При осуществлении рекурсивной сортировки, массив разбивается на две части, и каждая из этих частей сортируется отдельно. Таким образом, шаг рекурсии занимает O(nlog(n)) времени. Всего шагов рекурсии log(n), так как далее сортируем элементы находящиеся на четных/нечетных позициях отедльно. Итого, общая сложность последовательного четно-нечётного слияния Бэтчера алгоритма сортировки составляет O(nlog2(n)).
1.7 Информационный граф
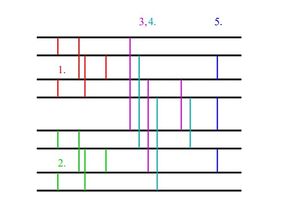
На рисунке изображена чётно-нечетная сортировка Бэтчера для 8 элементов. Можно заметить, что каждый рабочий поток нарисован в виде вертикальной линии. Линии соединяют попарно сортируемые элементы. Цветом разделены основные блоки в нашем алгоритме: 1.Сортировка первой половины списка 2. Сортировка второй половины списка 3.Сортировка ключей с нечетным индексом 4. Сортировка ключей с четным индексом 5. Сравнение между элементами на соседних позициях
1.8 Ресурс параллелизма алгоритма
В целом, алгоритм сортировки дает выигрыш по времени при использовании параллелизма. Алгоритм четно-нечетной сортировки Бэтчера можно распараллелить на любое число процессов, являющееся степенью числа двойки. Это позволит сократить время выполнения за счет увеличения количества MPI процессов. Однако, необходимо помнить, что так же будет затрачиваться время на создание процессов и обмен сообщениями между ними. Поэтому выгодно использовать распараллеливание на большое число процессов в основном для очень больших длин массивов данных, в ином случае затраты на использование MPI процессов не будут сильно заметны и временные затраты не будут слишком отличается от последовательного выполнения. На рисунке 2 каждый процесс пронумерован и выделен зеленым цветом. Из диаграммы видно, что на вход подается неотсортированный массив из 8 элементов. Как мы видим, необходимо 19 операций сравнения, чтобы массив отсортировать. В процессах 1-10, элементы сортируются в двух равных по длине подпоследовательностях, а потом объединяются. С 11 по 16 процесс идет сортировка на четных/нечетных позициях, и в заключительных 17, 18 и 19 состояниях происходит сравнение соседних элементов. В реализации 5 -10 процессов может использоваться функция MPI_recv().
1.9 Входные и выходные данные алгоритма
Исходные данные: последовательность a0, ..., an-1 длины n > 1 , где половины a0, ..., an/2-1 and an/2, ..., an-1 отсортированы (n является степенью 2) [4] Выходные данные: отсортированная последовательность
1.10 Свойства алгоритма
Временная сложность алгоритма: • При последовательной реализации O(nlog2(n)) • При параллельной реализации O(log2(n)) Использование памяти: • В худшем случае составит O(nlog2(n)) • В случае использования параллелизма количество памяти зависит от реализации, числа процессов и размера массива Преимущества: • Количество сравнений меньше, чем у битонной сортировки Недостатки: • Непопулярный алгоритм • Относительно сложно реализовывается и мало материалов, малое количество готовых реализаций кода можно найти
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Масштабируемость алгоритма и его реализации
В целом алгоритм четно-нечетной сортировки Бэтчера можно распараллелить на любое число процессов, являющееся степенью числа двойки. Это позволит сократить время выполнения за счет увеличения количества MPI процессов. Однако, необходимо помнить, что так же будет затрачиваться время на создание процессов и обмен сообщениями между ними. Поэтому выгодно использовать распараллеливание на большое число процессов в основном для очень больших длин массивов данных, в ином случае затраты на использование MPI процессов не будут сильно заметны и временные затраты не будут слишком отличается от последовательного выполнения. Реализованный алгоритм запускался на суперкомпьютере Ломоносов 2.
2.4 Динамические характеристики и эффективность реализации алгоритма
2.5 Выводы для классов архитектур
2.6 Существующие реализации алгоритма
Вариант реализации алгоритма можно посмотреть на https://copyprogramming.com/howto/batcher-s-odd-even-merge-sort https://cs.wmich.edu/gupta/teaching/cs5260/5260Sp15web/lectureNotes/Odd-even%20mergesort%20basics.pdf https://sudonull.com/post/97026-Butchers-even-odd-merge-sort Данные реализации предложены на языках C++, C .Время работы составляет O(log2n), объем занимаемой памяти O(nlogn)