Участник:Sfedotov/Алгоритм Ланцоша с полной переортогонализацией
 | Эта работа ждет рассмотрения преподавателем Дата последней правки страницы: 16.10.2016 Авторы этой статьи считают, что задание выполнено. |
| Алгоритм Ланцоша с полной переортогонализацией | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(n^2)[/math] |
| Объём входных данных | [math]\frac{n(n + 1)}{2}[/math] |
| Объём выходных данных | [math]m(n + 1)[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(m)[/math] |
| Ширина ярусно-параллельной формы | [math]O(n^2)[/math] |
Автор описания: Федотов С.А.
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
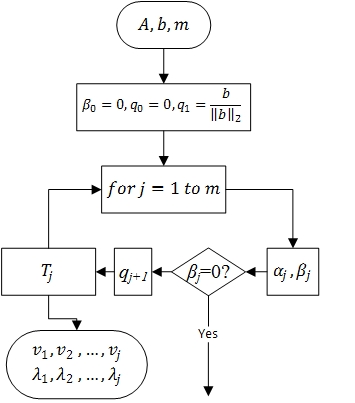
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Алгоритм Ланцоша - итерационный метод вычисления собственных значений и собственных векторов вещественной симметричной матрицы A, основными преимуществами которого являются малые затраты памяти и вычислительных ресурсов. Применяется для сильно больших матриц. Прямой алгоритм, разработанный Корнелием Ланцошом, адаптирует степенной метод поиска наибольших собственных значений и собственных векторов линейной системы размерности n с ограниченным числом итераций, m, где m много меньше n. Метод достаточно эффективный с вычислительной точки зрения, однако в первоначальном виде неустойчив. В 1970, Ojalvo и Newman[1] показали как добиться устойчивости и применили метод для расчета очень крупных инженерных конструкций, подверженных динамической нагрузке. В своей работе авторы также предложили способ выбора начального приближения и эмпирически оценили число итераций m. Оригинальный метод не учитывает влияние ошибок округления, поэтому на практике для арифметики с плавающей точкой используется вариант метода Ланцоша с полной переортогонализацией. Существует более быстая модификация при почти такой же точности - Алгоритм Ланцоша с выборочной ортогонализацией. В настоящее время метод широко используется в различных технических областях и имеет множество своих вариантов.
1.2 Математическое описание алгоритма
Алгоритм Ланцоша соединяет в себе метод Ланцоша для построения крыловского подпространства с процедурой Рэлея-Ритца. Входными данными алгоритма служат квадратная матрица A=ATи вектор начального приближения b. Мы пытаемся найти трехдиагональную симметричную матрицу Tk=QkTAQk, собственные значения которой приближают собственные значения матрицы A. Иными словами на k-м шаге из ортонормированных векторов Ланцоша строится матрица Qk = [q1,q2,...,qk,] и в качестве приближенных собственных значений матрицы A принимаются числа Ритца. Пусть Tk=V[math]\Lambda[/math]VT есть спектральное разложение матрицы Tk, столбцы матрицы QkV рассматриваются как приближения к соответсвующим собственным векторам матрицы A[2]: [math] \begin{align} q_1 = & \frac{b}{\|b\|_2},\; \beta_0 = 0,\; q_0 = 0\\ for \; & j = 1 \; to \; k \\ & z = Aq_j\\ & \alpha_j = q^T_j z\\ & z=z-\alpha_jq_j-\beta_{j-1}q_{j-1}\\ & z = z - \sum^{j-1}_{i=1}\left(z^Tq_i\right)q_i,\;z = z - \sum^{j-1}_{i=1}\left(z^Tq_i\right)q_i \\ & \beta_j = \|z\|_2\\ & q_{j+1} = \frac{z}{\beta_j}\\ end \; & for \end{align} [/math]
Диагональные элементы обозначены как [math]\alpha_j=t_{jj}[/math], а элементы побочной диагонали [math]\beta_j=t_{j-1,j}=t_{j,j-1}[/math]. После каждой итерации мы вычисляем [math]\alpha_j, \beta_j[/math], из которых строится матрица [math]T_j = \begin{pmatrix} \alpha_1 & \beta_2 & & & & 0 \\ \beta_2 & \alpha_2 & \beta_3 & & & \\ & \beta_3 & \alpha_3 & \ddots & & \\ & & \ddots & \ddots & \beta_{j-1} & \\ & & & \beta_{j-1} & \alpha_{j-1} & \beta_j \\ 0 & & & & \beta_j & \alpha_j \\ \end{pmatrix}[/math]
Полная переортогонализация соответствует повторному проведению процесса ортогонализации Грама-Шмидта для того, чтобы почти гарантировать, что [math]z[/math] будет ортогонален векторам q1,q2,...,qj-1. Потеря ортогонализации не заставляет алгоритм вести себя непредсказуемым образом. В качестве расплаты мы приобретаем повторные копии сошедшихся чисел Ритца. То есть для больших k матрица Tk может иметь не одно собственное значение, очень близкое к [math]\lambda_i(A)[/math], но много таких собственных значений. Нахождение собственных значений и собственных векторов трехдиагональной матрицы значительно проще чем их вычисление для исходной матрицы. Например при помощи MRRR алгоритма они могут быть вычислены за O(k2) флопов.
1.3 Вычислительное ядро алгоритма
За один шаг алгоритма можно выделить следующие вычислительные ядра:
- умножение исходной матрицы на вектор [math]z=Aq_j[/math]
- процесс ортогонализации Грама-Шмидта [math]z = z - \sum^{j-1}_{i=1}\left(z^Tq_i\right)q_i[/math]
1.4 Макроструктура алгоритма
Основные состовляющие алгоритма это умножение матрицы на вектор, процесс переортогонализации и поиск всех собственных значений и всех собственных векторов симметричной трехдиагональной матрицы
1.5 Схема реализации последовательного алгоритма
1.6 Последовательная сложность алгоритма
Для вычисления k-й итерации алгоритма Ланцоша с полной переортогонализации требуется выполнить:
- n+2k умножений вектора на вектор
- 2k умножение вектора на константу
- 2k сложения векторов
- O(k2) операций на разложение матрицы Tk
Легко проверить, что m шагов этого алгоритма потребуют O(m2n) флопов и O(mn) слов памяти
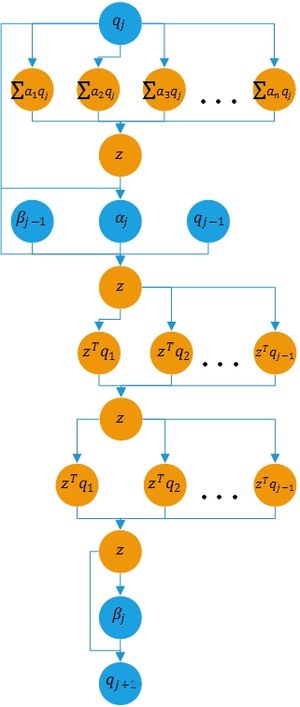
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
Алгоритм Ланцоша с полной переортогонализацией в целом последовательный. На j-м шаге вычисляются числа [math]\alpha_j, \beta_j[/math] и ортонормированный вектор [math]q_{j+1}[/math], которые служат входными данными для j+1-го шага. Нетрудно заметить, что процесс переортогонализации j-го приближения может быть вычислен параллельно
1.9 Входные и выходные данные алгоритма
Входные данные: матрица [math]A\in\mathbb{R}^{n\times n}[/math]. Дополнительные ограничения:
- [math]A[/math] – симметричная матрица, т. е. [math]a_{ij}= a_{ji}, i, j = 1, \ldots, n[/math].
Объём входных данных: [math]\frac{n (n + 1)}{2}[/math]
Выходные данные:
- вектор приближенных собственных значений матрицы [math]\Lambda[/math] (элементы [math]\lambda_{ii}[/math]).
- приближения к собственным векторам [math]v_i,i=1,\ldots, m [/math]
Объём выходных данных: [math] m(n+1) [/math].
1.10 Свойства алгоритма
- Метод Ланцоша не требует хранения исходной матрицы полным массивом: метод использует исходную матрицу только в операциях умножения матрицы на вектор, что позволяет эффективно использовать разреженность матрицы или регулярность структуры матрицы. Поэтому метод Ланцоша может быть использован для матриц таких больших порядков, когда методы вращений и отражений не могут быть применены.
- Часто уже при небольшом [math]( j \sim 2 \sqrt{n})[/math] числе шагов метода крайние пары Ритца [math](\lambda_i,v_i|[v_1,v_2,...,v_j]=Q_jV)[/math] оказываются хорошими приближениями к крайним собственным парам исходной матрицы (имеются теоретические оценки скорости сходимости, обосновывающие эту возможность), а именно крайние собственные пары часто и нужны.
- Если известно, что искомые (крайние) собственные значения являются кратными, то вместо простого метода Ланцоша имеет смысл использовать блочный (ленточный) метод Ланцоша. В блочном методе Ланцоша в отличие от простого метода вместо одного начального вектора берется ортонормированная система из l, l > 1, векторов. Аналогом векторов [math]z,q_i[/math] простого метода в блочном являются прямоугольные матрицы размера n * l, аналогом скаляров [math]\beta_i, \alpha_i[/math] - квадратные матрицы порядка l, аналогом трехдиагональной матрицы Ti - ленточная матрица с полушириной ленты l. Такие ленточные матрицы могут иметь собственные значения кратности вплоть до l. Поэтому блочный метод с l начальными вектрами используется, когда известно, что среди искомых собственных значений многие имеют кратность l. При использовании блочного метода все копии кратного собственного значения будут найдены на одном шаге, в простом же методе Ланцоша они определяются последовательно. Блочный метод, как и Алгоритм Ланцоша для точной арифметики может быть дополнен выборочной ортогонализацией.