Участник:Igor.orpanen/Плотностный алгоритм кластеризации (DBSCAN)

Эта работа ждет рассмотрения преподавателем Дата последней правки страницы: 16.10.2016 Авторы этой статьи считают, что задание выполнено.

Плотностный алгоритм кластеризации (DBSCAN)
Последовательный алгоритм
Последовательная сложность	[math]O(n \log n)[/math]
Объём входных данных	[math]n[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(|S| \log S)[/math]
Ширина ярусно-параллельной формы	[math]O(k)[/math]

Автор описания: Орпанен И.С.

1 ЧАСТЬ. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Задача кластеризации заключается в разделении исходной выборки данных на непересекающиеся группы, причём объекты из одной группы должны обладать сходством, которое чаще всего характеризуется функцией расстояния между объектами, например, Евклидово расстояние. Основными отличительными особенностями кластеризации являются:

• Отсутствие обучающей выборки, т.е. объектов, принадлежащих предопределённому кластеру
• Неизвестное число кластеров
• Значительная зависимость от выбранной функции расстояния между объектами

Плотностный алгоритм кластеризации DBSCAN (Density-based spatial clustering of applications with noise) является алгоритмом кластеризации, позволяющим находить кластеры произвольной формы в метрическом пространстве. Он был предложен учёными Martin Ester, Hans-Peter Kriegel, Jörg Sander и Xiaowei Xu в 1996 году.

Основной идеей алгоритма DBSCAN является представление объектов кластера в виде группы точек в метрическом пространстве, являющихся вершинами одного связного графа. Причём две точки в таком графе соединеняются ребром только в том случае, если расстояние между ними в заданной метрике не превышает определённого расстояния. Если рядом с некоторым объектом нет достаточно близких соседей, то он признаётся выбросом.

1.2 Математическое описание алгоритма

Входные данные: множество объектов [math]X[/math], для которых задана метрическая функция расстояния [math]\rho[/math].

Выходные данные: размеченное множество объектов, где каждому объекту сопоставлен порядковый номер кластера, в который попал данный объект, либо объект отмечается как выброс (шум).

Параметры алгоритма:

• [math]\varepsilon[/math] - максимальное расстояния между соседними объектами,
• [math]minPts[/math] - минимальное количество соседних объектов, необходимых для образования кластера.

1.2.1 Определения

• Объект [math]p \in X[/math] называется ядровым, если в [math]\varepsilon[/math]-окрестности точки [math]p[/math] находятся [math]MinPts[/math] объектов (включая сам объект [math]p[/math]). Эти объекты называются напрямую достижимыми из [math]p[/math].
• Объект [math]q \in X[/math] называется достижимым из [math]p[/math], если существует путь [math]p_1,...,p_n[/math], где [math]p_1 = p[/math] и [math]p_n = q[/math], а каждый объект [math]p_{i+1}[/math] напрямую достижим из [math]p_i[/math]. Таким образом вся объекты в пути, кроме объекта [math]q[/math], должны быть ядровыми.
• Выбросами (или шумом) называются все объекты, недостижимые ни из одного другого объекта.
• Кластером является множество ядровых точек, достижимых друг из друга, а также граничные неядровые точки, которые достижимы из любой ядровой точки кластера.

1.2.2 Описание алгоритма

1. Выбираем необработанный объект [math]p[/math].
2. Отмечаем объект [math]p[/math] как обработанный.
3. Находим соседние объекты в [math]\varepsilon[/math]-окрестности объекта [math]p[/math].
4. Сравниваем количество соседних объектов с [math]MinPts[/math], определяя, является ли [math]p[/math] ядровым объектом
   • Если объект [math]p[/math] является ядровым, то создаём новый кластер и запускаем поиск в ширину из данного объекта по другим непосещённым объектам, находя все объекты кластера.
   • Если объект [math]p[/math] не является ядровым, то отмечаем его как выброс (или шум).
5. Если присутствуют необработанные объекты, то возвращаемся к шагу 1.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма представляет собой поиск соседних объектов, попадающих в [math]\varepsilon[/math]-окрестность каждого объекта из множества [math]X[/math]. Для достижения наибольшей производительности используется предварительные расчёты и построение специальных структур данных, позволяющих находить соседние объекты за логарифмическое время.

1.4 Макроструктура алгоритма

1.4.1 Вычисление расстояния между объектами

Для вычисления расстояния [math]\rho[/math] между двумя объектами из кластеризуемого множества используется метрика. В большинстве случаев вычисляется метрика Евклида: [math]\rho(\mathbf{p}, \mathbf{q})=\sqrt{(p_1-q_1)^2+(p_2-q_2)^2+\dots+(p_n-q_n)^2} = \sqrt{\sum_{k=1}^n (p_k-q_k)^2}[/math]

В качестве альтернативного примера можно привести метрику Манхэттена, введённую Германом Минковским: [math]\rho(\mathbf{p}, \mathbf{q}) = \sum_{i=1}^n |p_i-q_i|,[/math]

1.4.2 Поиск соседних объектов в [math]\varepsilon[/math]-окрестности

Для поиска соседних объектов может быть использован простой перебор всех известных объектов, однако последовательная сложность такого алгоритма будет равна [math]O(n^2)[/math]. Для ускорения работы алгоритма обычно используются специальные структуры данных, такие как r-tree, k-d tree, ball tree, vantage-point tree и т.д. Эти структуры данных могут быть построены за время [math]O(n \log n)[/math], тем самым снизив общую временную сложность алгоритма.

1.5 Схема реализации последовательного алгоритма

Схема реализации алгоритма DBScan может быть описана на псевдокоде в терминах оригинальной статьи:

DBSCAN(X, Eps, MinPts) {
   C = 0
   for P ∈ X {
      if P is visited
         continue
      mark P as visited
      PNeighbors = regionQuery(P, Eps)
      if len(PNeighbors) < MinPts
         mark P as noise
      else {
         C = next cluster
         expandCluster(P, PNeighbors, C, Eps, MinPts)
      }
   }
}

expandCluster(P, PNeighbors, C, Eps, MinPts) {
   add P to cluster C
   for each point Q ∈ PNeighbors { 
      if Q is not visited {
         mark Q as visited
         QNeighbors = regionQuery(Q, Eps)
         if len(QNeighbors) >= MinPts
            PNeighbors = PNeighbors ∪ QNeighbors
      }
      if Q is not in any cluster
         add Q to cluster C
   }
}

regionQuery(P, Eps)
   return all points within P's Eps-neighborhood (including P)

1.6 Последовательная сложность алгоритма

Последовательная сложность алгоритма DBSCAN определяется сложностью его вычислительного ядра, то есть поиска соседних объектов в [math]\varepsilon[/math]-окрестности для каждого объекта из исходного множества [math]X[/math]. Алгоритм посешает каждый объект из множества [math]X[/math] ровно один раз, и это приводит к вызову функции regionQuery. В случае подсчёта расстояний до каждого объекта вызов функции regionQuery имеет последовательную сложность [math]O(n)[/math], а значит общая последовательная сложность равна [math]O(n^2)[/math]. В случае использования вспомогательной структуры данных функция regionQuery может иметь сложность [math]O(\log n)[/math], таким образом снизив общую последовательную сложность алгоритма до [math]O(n \log n)[/math].

1.7 Информационный граф

Параллельные реализации алгоритма DBSCAN всегда используют специальные пространственные структуры данных, такие как k-d tree, r-tree и vantage-point tree. Построение этих структур данных может быть распараллелено путём разделения множества объектов [math]X[/math] на части [math]X_i[/math], где [math]i=\overline{1,k}[/math].

1.7.1 PDBSCAN

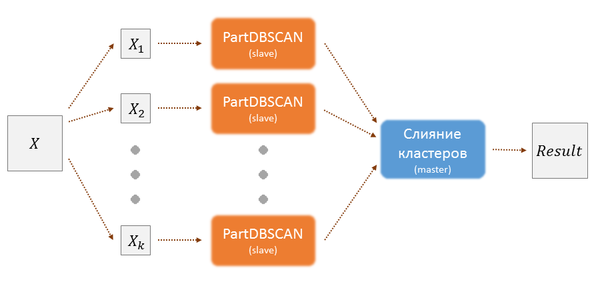
Первый рассматриваемый параллельный алгоритм PDBSCAN был предложен ещё в 1999 году.. Его основной особенностью является master-slave архитектура. Используются распределённые dR*-деревья, которые позволяют разбить метрическое пространств на области и распределить вычисления между slave-машинами. Затем в каждой из этих областей происходит поиск кластеров, а также определяется необходимость слияния с кластерами из других областей с помощью алгоритма PartDBSCAN. Затем slave-машины отправляют результаты своих вычислений на master-машину, которая сливает необходимые кластеры вместе и завершает выполнение распределённого алгоритма. Информационный граф изображён на рисунке 1.

Рис.1. Информационная структура алгоритма PDBSCAN

1.7.2 PDSDBSCAN

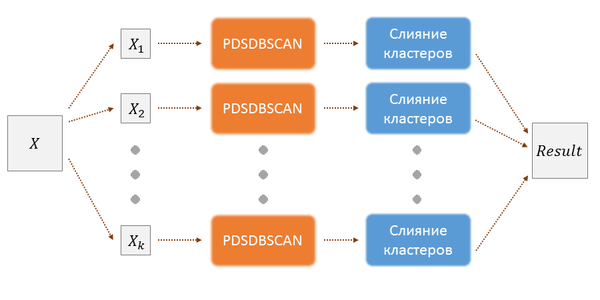
Другой параллельный алгоритм PDSDBSCAN был предложен в 2012 году. Его авторы отмечают недостатки master-slave архитектуры и предлагают полностью распределённый алгоритм, основанный на структуре данных из непересекаюшихся множеств, которая позволяет операцию слияния этих множеств. Это позволяет производить слияние кластеров без master-машины и значительно повысить производительность распределённого алгоритма. Информационный граф изображён на рисунке 2.

Рис.2. Информационная структура алгоритма PDSDBSCAN

1.8 Ресурс параллелизма алгоритма

Ширина ярусно-параллельной формы обоих алгоритмов PDBSCAN и PDSDBSCAN равна [math]O(k)[/math], где [math]k[/math] - это количество частей, на которые разбивается исходный набор объектов. Высота ярусно-параллельной платформы у обоих алгоритмов одинакова и равна [math]O(|S| \log S)[/math], где [math]S=\max_{1 \leq i \leq k} |X_i|[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: множество объектов [math]X[/math], для которых задана метрическая функция расстояния [math]\rho[/math]. Объём входных данных: [math]n[/math].

Выходные данные: размеченное множество объектов, где каждому объекту сопоставлен порядковый номер кластера, в который попал данный объект, либо объект отмечается как выброс (шум). Объём выходных данных: [math]n[/math].

Количество кластеров и шума в выходных данных зависят от входных данных и параметров алгоритма. Более компактное расположение объектов, меньшие значения параметра [math]MinPts[/math], большие значения параметра [math]\varepsilon[/math] ведут к образования меньшего числа кластеров, вплоть до одного единственного кластера. Если варьировать данные параметры в противоположную сторону, то количество кластеров и шумовых объектов будет расти, вплоть до момента, когда все объекты будут являться шумом.

1.10 Свойства алгоритма

• Алгоритм находит заранее неизвестное число кластеров произвольной формы.
• Алгоритм работает в условиях зашумлённых данных, выделяя выбросы в отдельную категорию объектов.
• Алгоритм обладает сбалансированностью вычислительного процесса относительно всех типов операций при разбиении входных данных на части примерно одинакового размера.
• Алгоритм не является детерминированным, так как в некоторых случаях граничные точки могут попасть в несколько различных кластеров, что зависит от порядка их формирования. Однако это не оказывает значительного влияния на результаты работы алгоритма. Существует вариация алгоритма DBSCAN*, которая относит все граничные точки к шуму, тем самым достигая полной детерминированности.
• Качество работы алгоритма сильно зависит от используемой метрики, а также от правильно выбранных параметров [math]MinPts[/math] и [math]\varepsilon[/math] для заданной предметной области. В частности для объектов в пространстве большой размерности при использовании метрики Евклида имеет место проклятие размерности.
• Алгоритм плохо работает для разнородных данных, состоящих из кластеров разной плотности, так как тогда параметры алгоритмы [math]MinPts[/math] и [math]\varepsilon[/math] не могут быть выбраны оптимальным образом.

2 ЧАСТЬ. Программная реализация алгоритма

2.7 Существующие реализации алгоритма

Реализация	Технологии	Лицензия	Посдедовательная сложность	Структуры данных	Метрики	Параллельность
Scikit learn	Python	BSD 3	[math]O(n \log n)[/math]	k-d tree, ball tree	Любые	Есть
alitouka/spark_dbscan	Scala, Spark	GPLv2	[math]O(n \log n)[/math]	r-tree	Euclidean	Есть
irvingc/dbscan-on-spark	Scala, Spark	GPLv2	[math]O(n \log n)[/math]	r-tree	Euclidean	Есть
propanoid/DBSCAN	C++, Boost, OpenMP	ABRMS	[math]O(n \log n)[/math]	vantage-point tree	Euclidean	Есть
CRAN	R, C++	GPLv3	[math]O(n \log n)[/math]	k-d tree	Euclidean	Нет
Weka	Java	GPLv3	[math]O(n^2)[/math]	-	Euclidean, Manhattan	Нет
Apache Commons	Java	Apache 2.0	[math]O(n^2)[/math]	-	Euclidean	Нет
choffstein/dbscan	Python	-	[math]O(n^2)[/math]	-	Euclidean	Нет