Участник:Арутюнов А.В.

Решение системы нелинейных уравнений методом Ньютона
Последовательный алгоритм
Последовательная сложность	[math]O(n^3) [/math] - одна итерация
Объём входных данных	[math]n^2 + n[/math] функций от [math]n[/math] переменных, [math]n[/math] мерный вектор, [math]x^0[/math] - начальное приближение, ε - точность решения.
Объём выходных данных	[math]n[/math]-мерный вектор вещественных чисел
Параллельный алгоритм
Высота ярусно-параллельной формы	[math][/math]
Ширина ярусно-параллельной формы	[math][/math]

Автор описания: Арутюнов А.В., Жилкин А.С.

Решение системы нелинейных уравнений методом Ньютона

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Метод Ньютона для решение систем нелинейных уравнений - обобщение классического метода Ньютона Это итерационный численный метод нахождения корня (нуля) заданной функции. Модификацией метода является метод хорд и касательных.

Классический метод Ньютона или касательных заключается в том, что если [math]x_n[/math] — некоторое приближение к корню [math]x_*[/math] уравнения [math]f(x)=0[/math], [math]f(x) \in C^1[/math], то следующее приближение определяется как корень касательной [math] f(x)[/math] к функции, проведенной в точке [math]x_n[/math].

Метод был предложен Исааком Ньютоном в 1669 году. Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации.

1.2 Математическое описание алгоритма

Идея метода заключается в линеаризации уравнений системы

[math] \left\{\begin{matrix}f_1(x_1, ..., x_n) = 0 \\ f_2(x_1,...x_n)=0, \\ ..., \\ f_n(x_1, ..., x_n) = 0, \end{matrix}\right. [/math]

Что позволяет свести исходную задачу СНУ(система нелинейных уравнений) к многократному решению системы линейных уравнений.

Пусть известно приближение [math](x_i)^{(k)}[/math] решения системы нелинейных уравнений [math](x_i)^*[/math].Введем в рассмотрение поправку [math]\Delta x_i[/math] как разницу между решением и его приближением: [math] \Delta x_i = (x_i)^* -(x_i)^{(k)} \Rightarrow (x_i)^*=(x_i)^{(k)} + \Delta x_i, i=\overline{(1,n)} [/math]

Подставим полученное выражение для [math](x_i)^*[/math] в исходную систему.

[math] \left\{\begin{matrix} f_1((x_1)^{(k)} + \Delta x_1, (x_2)^{(k)}+ \Delta x_2, ..., (x_n)^{(k)} + \Delta x_n) = 0, \\ f_2((x_1)^{(k)} + \Delta x_1, (x_2)^{(k)} + \Delta x_2, ..., (x_n)^{(k)} + \Delta x_n) = 0, \\ ... \\ f_n((x_1)^{(k)} + \Delta x_1, (x_2)^{(k)} + \Delta x_2, ..., (x_n)^{(k)} + \Delta x_n) = 0, \end{matrix}\right. [/math]

Неизвестными в этой системе нашейных уравнений являются поправки [math]\Delta x_i [/math]. Для определения [math]\Delta x_i [/math] нужно решить эту систему. Но решить эту задачу так же сложно, как и исходную. Однако эту систему можно линеаризовать и, решив её, получить приближённые значения поправок [math]\Delta x_i[/math] для нашего приближения, т.е. [math]\Delta (x_i)^{(k)}[/math]. Эти поправки не позволяют сразу получить точное решение [math](x_i)^*[/math], но дают возможность приблизиться к решению, - получить новое приближение решения [math]((x_i)^{(k+1)} = ((x_i)^{(k)} + ( \Delta x_i)^{(k)}, i = \overline{(1,n)}[/math]

Для линеаризации системы следует разложить функцию [math]f_i[/math] в ряды Тейлора в окрестности [math](x_i)^k[/math], ограничиваясь первыми дифференциалами. Полученная система имеет вид:

[math]\sum_{i=1}^n\frac{ \partial f_i({x_1}^{(k)}, {x_2}^{(k)}, ..., {x_n}^{(k)})}{ \partial x_i} \Delta {x_i}^{(k)}= -f_j({x_1}^{(k)}, {x_2}^{(k)}, ..., {x_n}^{(k)}), j=\overline{(1,n)}[/math]

Все коэффициенты этого уравнения можно вычислить, используя последнее приближение решения [math](x_i)^{(k)}[/math]. Для решения системы линейных уравнений при [math]n=2,3[/math] можно использовать формулы Крамера, при большей размерности системы [math]n[/math] - метод исключения Гаусса.

Значения поправок используются для оценки достигнутой точности решения. Если максимальная по абсолютной величине поправка меньше заданной точности [math]\varepsilon[/math], расчет завершается. Таким образом, условие окончания расчета:

[math]\delta =\min_{ i=\overline{(1,n)}}|\Delta {x_i}^{(k)}|[/math]

Можно использовать и среднее значение модулей поправок:

[math]\delta = \frac{1}{n}\sum_{i=1}^n |\Delta x_i|\lt \varepsilon [/math]

В матричной форме систему можно записать как:

[math]W(\Delta X^k)*X^{(k)} = -F(X^k)[/math]

где [math]W(x)[/math] - матрица Якоби(производных):

[math]W(x)=(\frac{\partial f_j}{\partial x_i})_{n,n}= \left\{\begin{matrix}(\frac{\partial f_1}{\partial x_1} \frac{\partial f_1}{\partial x_2} ... \frac{\partial f_1}{\partial x_n}) \\ ... ... ... ... \\( \frac{\partial f_n}{\partial x_1} \frac{\partial f_n}{\partial x_2} ... \frac{\partial f_n}{\partial x_n} ) \end{matrix}\right. [/math]

[math]\Delta X^{(k)}= \left\{\begin{matrix} \Delta (x_1)^{(k)} \\ \Delta (x_2)^{(k)} \\ ... \\ \Delta (x_n)^{(k)} \end{matrix}\right. [/math]

[math]F(x)[/math] - вектор-функция

[math]W(X^{(k)})[/math] - матрица Якоби, вычисленная для очередного приближения [math]F(X^{(k)})[/math] - вектор-функция, вычисленная для очередного приближения

Выразим вектор поправок [math]X^{(k)}=-W^{-1}(X^{(k)})*F(X^{(k)})[/math] :

[math]W^{-1}[/math], где [math]W^{-1}[/math]

Окончательная формула последовательных приближений метода Ньютона решения СНУ в матричной форме имеет вид:

[math]X^{(k+1)}=X^{(k)}=W^{-1}(X^{(k)})*F(X^{(k)})[/math]

1.3 Вычислительное ядро алгоритма

Основная вычислительная нагрузка приходится на

1) Решение СЛАУ: [math]F(X^{(k)})=\frac{\partial F(x^{(k)})}{\partial x} \Delta x^{(k)}[/math]

2)Численное вычисление Якобиана(если производные не даны): [math]\frac{\partial F(x^{(k)})}{\partial x}[/math]

1.4 Макроструктура алгоритма

Данный алгоритм использует два основных метода решения в каждой итерации, это нахождением матрицы Якоби и решение СЛАУ.

1.5 Схема реализации последовательного алгоритма

1)Задаётся размерность системы [math]n[/math], требуемая точность, начальное приближённое решение [math]X=(x_i)_n[/math]

2)Вычисляются элементы матрицы Якоби [math]W=\left( {\partial f_i\over \partial x_i} \right)_{n,n}[/math]

3)Вычисляется обратная матрица [math]W^{-1} [/math]

4)Вычисляются вектор функция [math]F=(f_i)_n, f_i=f_i(x_1, x_2,..., x_n), i=1,...,n [/math]

5)Вычисляются вектор поправок [math] \Delta X=W_{-1}*F [/math]

6)Уточняется решение [math]X_{n+1}=X_n+\Delta X[/math]

7)Оценивается достигнутая точность [math]\delta = \max_{i=1,n} \Delta x_i^k[/math]

8)Проверяется условие завершения итерационного процесса [math]\delta\lt =\varepsilon[/math]

1.6 Последовательная сложность алгоритма

Сперва стоит отметить, что итоговая сложность алгоритма зависит от того, насколько быстро он будет сходиться. Это в свою очередь зависит от заданного начального приближения [math]x^0[/math] и от условия остановки алгоритма [math]\varepsilon[/math]. Можно однако вычислить сложность одного шага итерации алгоритма.

Предполагаем, что у нас нет значений производных заданных функций

[math]f_1(.), f_2(.), ..., f_n(.)[/math].

Тогда используя формулу центральной разности для производной :

[math]f_i'(x) = (f(x+h) - f(x-h))/2h [/math],

мы находим приближённое значение производной в интересующей нас точке за 5 операций.

Учитывая, что в Якобиане содержится [math]n^2[/math] элементов - производные каждой функции по каждой переменной, - то для нахождения Якобиана нам суммарно требуется

[math]O(5n^2) = O(n^2)[/math]

операций. Сложность вычислений обратной матрицы

[math]W^{-1} [/math]

зависит от выбранного алгоритма решения полученной СЛАУ. Будем использовать метод Гаусса. В таком случае сложность составит

[math]O(n^3)[/math].

Таким образом сложность вычислительного ядра алгоритма составляет

[math]O(n^2)+O(n^3) = O(n^3)[/math]

для одного шага алгоритма.

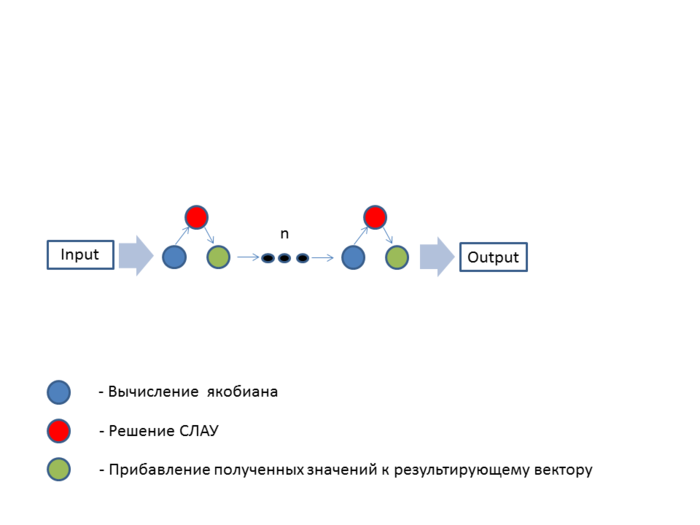
1.7 Информационный граф

Рис.1 Информационный граф алгоритма

1.8 Ресурс параллелизма алгоритма

Не смотря на то, что метод Ньютона является методом последовательных итераций, его можно распараллелить. Ресурс для параллелизма заключается в решение СЛАУ и вычислении Якобианов. Рассмотрим решение параллельным методом Гаусса на [math]p[/math] процессорах.

Сложность вычисление элементов матрицы Якоби - производных [math]\frac{\partial F(x^{(k)})}{\partial x}[/math] в случае, если они не заданы будет - [math]O(n^2/p)[/math].

Решение СЛАУ [math]F(X^{(k)}) = \frac{\partial F(x^{(k)})}{\partial x} \Delta x^{(k)}[/math] одним из параллельных методов имеет сложность [math]O(n^3/p)[/math].

Пусть алгоритм имеет [math]N[/math] итераций, тогда итоговая сложность будет: [math]O(N \cdot \frac{n^3}{p})[/math]

1.9 Входные и выходные данные алгоритма

Входные данные: [math]n^2 + n[/math] функций от [math]n[/math] переменных, [math]n[/math] мерный вектор, [math]x^0[/math] - начальное приближение, [math]\varepsilon[/math] - точность решения.

Выходные данные: [math]n[/math] вещественных чисел

1.10 Свойства алгоритма

Для данного метода трудно универсально оценить соотношение последовательной и параллельной сложностей алгоритма, поскольку это зависит непосредственно от вида задаваемых нелинейных функций, способа решения СЛАУ и выбора начального приближения.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Как уже было отмечено выше, характеристики реализации алгоритма сильно зависят от выбранного способа нахождения матрицы Якоби и решения СЛАУ.

Для примера рассмотрим реализацию используя формулу центральной разности, приведённую в пункте 1.6 :

double derivative(double x, double h, std::function<double(double)> func) {
	return (func(x + h) - func(x - h)) / (2*h);
}

3 Литература

<references \> https://ru.wikipedia.org/wiki/Метод_Ньютона Тыртышников Е. Е. "Методы численного анализа" — М., Академия, 2007. - 320 c.

http://www.intuit.ru/studies/courses/4447/983/lecture/14931