Участник:Konstantin 013

Основные авторы описания: К.В.Телегин

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Данный алгоритм находит равновесие Нэша в игре двух лиц с конечным числом стратегий

1.2 Математическое описание алгоритма

Определим игру двух лиц. Пусть первый игрок имеет в своём распоряжении стратегии [math] x [/math] из множества стратегий [math] X [/math], а второй игрок стратегии [math] y [/math] из множества стратегий [math] Y [/math]. Будем рассматривать игру в нормальной форме. Это означает, что каждый из игроков выбирает стратегию, не зная выбора партнёра. Пару стратегий [math] (x, y) [/math] будем называть ситуацией. У первого игрока имеется функция выигрыша [math] F(x, y) [/math], а у второго [math] G(x, y) [/math], определённые на на множестве всех ситуаций [math] X × Y [/math]. каждый игрок стремится, по возможности, максимизировать свою функцию выигрыша. Таким образом, игра двух лиц в нормальной форме задаётся набором [math] \Gamma \langle X, Y, F(x, y), G(x, y) \rangle [/math]. Ситуация [math] (x^0, y^0) [/math] называется равновесием по Нэшу игры [math] \Gamma [/math] если: [math] \max_{x \in X} F(x, y^0) = F(x^0, y^0) \quad , \quad \max_{y \in Y} F(x^0, y) = G(x^0, y^0) [/math]

Иными словами, каждому из игроков невыгодно отколняться от ситуации равновесия.

В данной статье мы рассмотрим нахождение ситуаций равновесий Нэша в одном специальном случае для множеств [math] X, Y [/math]. Назовём игру [math] \Gamma [/math] биматричной, если [math] X, Y [/math] - конечные множества. тогда можно считать, что [math] X = [1, ..., n], Y = [1, ..., m] [/math], а [math] F, G [/math] - являются матрицами [math] R^{n × m} [/math]

1.3 Вычислительное ядро алгоритма

Сначала будет естественно для каждого столбца матрицы [math] F [/math] найти максимум в нём и для каждой строки матрицы [math] G [/math] найти максимум в ней. Т.е. мы ищем для каждого из [math] m [/math] векторов [math] R^n [/math] мы ищем максимум и для каждого из [math] n [/math] векторов [math] R^m [/math] мы ищем максимум. После этого для каждой ситуации [math] (x^0, y^0) [/math] несложно понять, является ли она равновесием Нэша: нужно просто проверить, что [math] F(x^0, y^0) [/math] - максимальный элемент в [math] y^0 [/math]-м столбце матрицы [math] F [/math] и [math] G(x^0, y^0) [/math] - максимальный элемент в [math] x^0 [/math]-ой строке матрицы [math] G [/math].

1.4 Макроструктура алгоритма

Алгоритм в качестве подзадачи многократно использует поис максимума в массиве (n раз для массиве длины m и ь раз для массиве длины n). Затем, для все возможных позиций проверяется, является она равноесием по нэшу, как это описывалось в разделе выше.

1.5 Схема реализации последовательного алгоритма

Данный код реализует последовательную версию алгоритма

#include <vector>
#include <algorithm>
#include <list>
#include <utility>


std::list<std::pair<int, int> > 
nash_equilibrium(
	const std::vector<std::vector<double> > &f,
	const std::vector<std::vector<double> > &g)
{
	std::list<std::pair<int, int> > res;

	int n = f.size();
	int m = g[0].size();

	std::vector<double> maxf(m);
	for (int i = 0; i < m; ++i) {
		maxf[i] = f[0][i];
		for (int j = 1; j < n; ++j) {
			maxf[i] = std::max(maxf[i], f[j][i]);
		}
	}

	std::vector<double> maxg(n);
	for (int i = 0; i < n; ++i) {
		maxg[i] = g[i][0];
		for (int j = 1; j < m; ++j) {
			maxg[i] = std::max(maxg[i], g[i][j]);
		}
	}


	for (int i = 0; i < n; ++i) {
		for (int j = 0; j < m; ++j) {
			if (f[i][j] == maxf[j] && g[i][j] == maxg[i]) {
				res.emplace_back(i, j);
			}
		}
	}

	return res;
}

1.6 Последовательная сложность алгоритма

Очевидно, сложность данного алгоритма будет [math] 2nm [/math]

1.7 Информационный граф

Для начала был создан граф поиска максимума для каждого столбца матрицы F. поиск максимума для каждой строки матрицы G делается аналогично.

Рис.1. поиск максимума для каждого столбца матрицы F

1.8 Ресурс параллелизма алгоритма

Для нахождения максимума в каждой из [math] n [/math] строк матрицы [math] F [/math] понадобится [math] m - 1 [/math] операция сравнения для вещественных чисел. Аналогично, для нахождения максимума в каждом из [math] m [/math] столбцов матрицы [math] G [/math] понадобится [math] n - 1 [/math] операция сравнения для вещественных чисел. Далее, для определения каждой ситуации на равновесие нужно просто сравнить значение в [math] F [/math] с максимумом в столбце и в [math] G [/math] с максимумом в строке, т.е. для каждой ситуации это [math] O(1) [/math], а так как, для каждой ситуации это независимые действия, при неограниченном числе ресурсов все вычисления имеют сложность [math] O(1) [/math].

1.9 Входные и выходные данные алгоритма

Входные данные: две матрицы [math] R^{n × m} [/math]

Выходные данные: список пар [math] (i, j) [/math], где [math] i \in [1 .. n], j \in [1 .. m] [/math]

2 Программная реализация алгоритма

2.1 Масштабируемость алгоритма и его реализации

Задача данного раздела - показать пределы масштабируемости алгоритма на различных платформах. Очень важный раздел. Нужно выделить, описать и оценить влияние точек барьерной синхронизации, глобальных операций, операций сборки/разборки данных, привести оценки или провести исследование сильной и слабой масштабируемости алгоритма и его реализаций.

Масштабируемость алгоритма определяет свойства самого алгоритма безотносительно конкретных особенностей используемого компьютера. Она показывает, насколько параллельные свойства алгоритма позволяют использовать возможности растущего числа процессорных элементов. Масштабируемость параллельных программ определяется как относительно конкретного компьютера, так и относительно используемой технологии программирования, и в этом случае она показывает, насколько может вырасти реальная производительность данного компьютера на данной программе, записанной с помощью данной технологии программирования, при использовании бóльших вычислительных ресурсов (ядер, процессоров, вычислительных узлов).

Ключевой момент данного раздела заключается в том, чтобы показать реальные параметры масштабируемости программы для данного алгоритма на различных вычислительных платформах в зависимости от числа процессоров и размера задачи . При этом важно подобрать такое соотношение между числом процессоров и размером задачи, чтобы отразить все характерные точки в поведении параллельной программы, в частности, достижение максимальной производительности, а также тонкие эффекты, возникающие, например, из-за блочной структуры алгоритма или иерархии памяти.

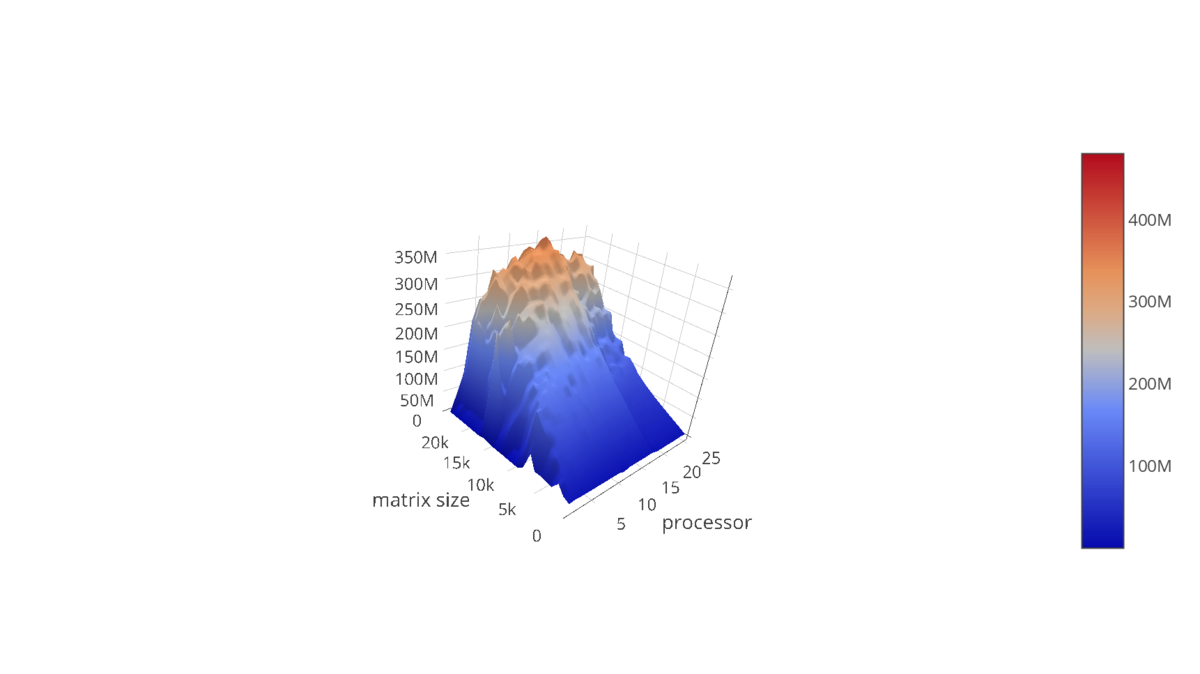
На рис.5. показана масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи. На графике хорошо видны области с большей производительностью, отвечающие уровням кэш-памяти.

Рис.1. brr F

2.2 Существующие реализации алгоритма

Данный код реализует параллельную версию алгоритма

#include <iostream>
#include <vector>
#include <list>
#include <algorithm>
#include <mpi.h>


using namespace std;


vector<vector<double> >
create_local_matrix(
	int n, 
	int m,
	int n_proc,
	int rank)
{
	int loc_n = rank < n % n_proc ? n / n_proc + 1 : n / n_proc;

	vector<vector<double> > F(loc_n, vector<double>(m));
	for (auto &i: F) {
		for (auto &j: i) {
			j = rand() % 1000;
		}
	}	

	return F;
}

vector<double> 
calc_max_in_rows(const vector<vector<double> > &G)
{
	vector<double> G_max(G.size());
	for (int i = 0; i < G.size(); ++i) {
		G_max[i] = G[i][0];
		for (int j = 1; j < G[i].size(); ++j) {
			G_max[i] = max(G_max[i], G[i][j]);
		}
	}

	return G_max;
}

vector<double>
calc_max_in_cols(const vector<vector<double> > &F)
{
	vector<double> F_max(F[0].size());

	for (int i = 0; i < F_max.size(); ++i) {
		F_max[i] = F[0][i];
		for (int j = 1; j < F.size(); ++j) {
			F_max[i] = max(F_max[i], F[j][i]);
		}
	}
	return F_max;
}



int
main(int argc, char *argv[])
{
	int n_proc;
	int rank;
	int n, m;



	MPI_Init(&argc, &argv);
	MPI_Comm_size(MPI_COMM_WORLD, &n_proc);
	MPI_Comm_rank(MPI_COMM_WORLD, &rank);



//reading and sending n and m;
	if (rank == 0) {
		// this is main process
		cin >> n >> m;
		if (n < m) {
			swap(n, m);
		}
	}

	MPI_Bcast(&n, 1, MPI_INT, 0, MPI_COMM_WORLD);
	MPI_Bcast(&m, 1, MPI_INT, 0, MPI_COMM_WORLD);

//Create and fill its part of matrices F and G
	srand(time(NULL));
	vector<vector<double> > F = create_local_matrix(n, m, n_proc, rank);
	vector<vector<double> > G = create_local_matrix(n, m, n_proc, rank);

//every process calculate max in every its rows of matrix G and columns of matrix F

	int loc_n = rank < n % n_proc ? n / n_proc + 1 : n / n_proc;

	//columns of F
	vector<double> loc_F_col_max = calc_max_in_cols(F);

	//and rows of G
	vector<double> loc_G_row_max = calc_max_in_rows(G);


//now we gather this local maximums in on common vector

	vector<double> F_max(m);
	MPI_Allreduce(loc_F_col_max.data(), F_max.data(), m, MPI_DOUBLE, MPI_MAX, MPI_COMM_WORLD);

//find nash equilibriums

	vector<pair<int, int> > loc_ans;

	for (int i = 0; i < loc_n; ++i) {
		for (int j = 0; j < m; ++j) {
			if (F[i][j] == F_max[j] && G[i][j] == loc_G_row_max[i]) {
				loc_ans.push_back(make_pair(i, j));
			}
		}
	}


	MPI_Finalize();

}