Участник:Sveta
Общая схема описания алгоритмов имеет следующий вид:
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Модель дуополии Штакельберга является развитием модели дуополии Курно. Если в модели Курно считается, что участники рынка не прогнозируют отклика конкурента на собственные действия, то в модели Штакельберга один участник рынка не прогнозирует поведения конкурента, а второй учитывает поведение первого, зная, что конкурент не ответит на его действия. Другими словами, второй участник рынка знает, что первый участник рынка ведет себя в соответствии с моделью Курно. [1]
1.2 Математическое описание алгоритма
Есть множество стратегий первого игрока [math] X [/math] и мноожество стратегий [math] Y [/math] второго игрока. Первым ходит игрок, называемый лидером, его стратегия [math] x \in X [/math]. Второй игрок, называемый подчиненным, ходит стратегией [math] y \in Y [/math]. У каждого игрока есть своя функция выигрыша. Для лидера это функция [math] H(x,y) [/math]. Для подчиненного [math] G(x,y) [/math]. Оба хотят максимизировать свой выигрыш, при условии лояльности(лояльность, это когда при условии одинакового выигрыша для второго, он максимизирует выигрыш первого) второго игрока по отношении к первому. Набор стратегий [math] (x^*,y^*) [/math] называется равновесием Штакельберга, если [math] y^* = R(x^*) [/math] есть наилучший ответ подчиненного на стратегию лидера, которая находится как решение задачи [math] H(x^*, y^*) = max H(x,R(x)) [/math]
1.3 Вычислительное ядро алгоритма
Для каждой стратегии первого, найдем множество наилучших ответов второго, благожелательных к первому. По всем найденым ответам второго, максимизируем выигрыш первого.
1.4 Макроструктура алгоритма
Данный алгоритм в качестве составных частей использует поиск максима в строке.
1.5 Схема реализации последовательного алгоритма
#include <vector>
#include <cstdlib>
#include <ctime>
using namespace std;
int main(int argc, char *argv[])
{
int n = strtol(argv[1], NULL, 10);
int m = strtol(argv[2], NULL, 10);
vector<vector<double>> H(n, vector<double>(m));
vector<vector<double>> G(n, vector<double>(m));
srand(time(NULL));
for(int i = 0; i < n; ++i) {
for(int j = 0; j < m; ++j) {
H[i][j] = rand();
G[i][j] = rand();
}
}
vector<int> ind(n);
for(int i = 0; i < n; ++i){
double max_in_line = H[i][0];
int ind_max = 0;
for(int j = 0; j < m; ++j){
if (G[i][j] > max_in_line) {
max_in_line = G[i][j];
ind_max = j;
} else if (G[i][j] == max_in_line) {
if (H[i][j] > H[i][ind_max]) {
ind_max = j;
max_in_line = G[i][j];
}
}
}
ind[i] = ind_max;
}
int str_h = 0;
for(int i = 0; i < n; ++i) {
if (H[i][ind[i]] > H[str_h][ind[str_h]]) {
str_h = i;
}
}
}
1.6 Последовательная сложность алгоритма
Для первой части - поиска наилучших стратегий для воторого потребуется [math] m * n [/math] операций сравенения.
Для второй части - поиска наилучших стратегий первого потребуется [math] n [/math] операций сравнения.
Таким образом результирующая сложность алгоритма - [math] n * m [/math] операций.
1.7 Информационный граф
Опишем граф алгоритма в виде рисунка.
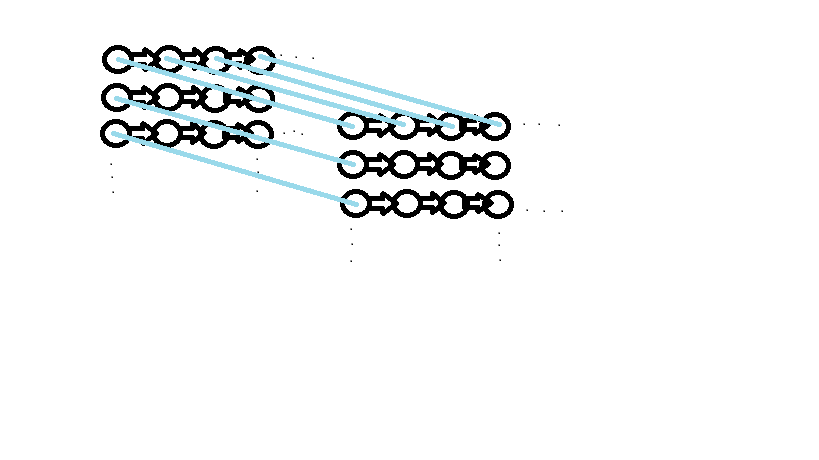
1.8 Ресурс параллелизма алгоритма
1.9 Входные и выходные данные алгоритма
Входными данными являются пара матриц [math] H(x,y) [/math], [math] G(x,y) [/math] одинакового размера [math]n * m [/math] (стратегии обоих игроков). Выходные данные это множество пар чисел [math] (x^*,y^*) [/math], где каждая из пар является равновесием по Штакельбергу в нашей дуаполии.
2 Программная реализация алгоритма
2.1 Масштабируемость алгоритма и его реализации
2.2 Существующие реализации алгоритма
3 Литература
- ↑ Шагин, В. Л. Теория игр с экономическими приложениями. Учебное пособие. — М., ГУ-ВШЭ, 2003.