Приложение 3

1 Обратная подстановка метода Гаусса (вещественный вариант)

1.1 Свойства и структура алгоритма

1.1.1 Общее описание алгоритма

Обратная подстановка - решение системы линейных алгебраических уравнений (СЛАУ) $Ux = y$ с верхней треугольной матрицей $U$. Матрица $U$ может быть одной из составляющих матрицы $A$ в каких-либо разложениях и получается либо из $LU$-разложения последней каким-либо из многочисленных способов (например, простое разложение Гаусса, разложение Гаусса с выбором ведущего элемента, компактная схема Гаусса, разложение Холецкого и др.), либо из других (например из QR-разложения). В силу треугольности $U$ решение СЛАУ является одной из модификаций общего метода подстановки и записывается простыми формулами.

В методом обратной подстановки назван также и метод решения СЛАУ с нижней треугольной матрицей. Там же отмечено, что в литературе иногда под обратной подстановкой имеют в виду, как и здесь, только решения СЛАУ с верхней треугольной матрицей, а решение нижних треугольных систем называют прямой подстановкой. Такой же системы названий будем придерживаться и здесь, во избежание одноимённого названия разных алгоритмов. Кроме того, обратная подстановка, представленная здесь, одновременно может быть частью метода Гаусса для решения СЛАУ, а именно - его обратным ходом, чего нельзя сказать про прямую подстановку.

Существует метод со сходным названием - Обратная подстановка с нормировкой. При том, что он решает, по существу, ту же задачу, что и простая обратная подстановка, его схема несколько сложнее. Это связано со специальными мерами по уменьшению влияния ошибок округления на результат. Обратная подстановка с нормировкой на данной странице не рассматривается.

1.1.2 Математическое описание алгоритма

Исходные данные: верхняя треугольная матрица $U$ (элементы $u_{ij}$), вектор правой части $y$ (элементы $y_{i}$).

Вычисляемые данные: вектор решения $x$ (элементы $x_{i}$).

Формулы метода:

$\begin{align} x_{n} & = y_{n}/u_{nn} \\ x_{i} & = \left (y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j} \right ) / u_{ii}, \quad i \in [1, n - 1]. \end{align}$

Существует также блочная версия метода, однако в данном описании разобран только точечный метод.

1.1.3 Вычислительное ядро алгоритма

Вычислительное ядро обратной подстановки можно составить из множественных (всего их $n-1$) вычислений скалярных произведений подстрок матрицы $U$ на уже вычисленную часть вектора $x$:

$\sum_{j = i+1}^{n} u_{ij} x_{j}$

в режиме накопления или без него, в зависимости от требований задачи, с их последующим вычитанием из компоненты вектора $y$ и деления на диагональный элемент матрицы $U$. В отечественных реализациях, даже в последовательных, упомянутый способ представления не используется. Дело в том, что даже в этих реализациях метода вычисление сумм типа

$y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j}$

в которых и встречаются скалярные произведения, ведутся не в порядке «вычислили скалярное произведение, а потом вычли его из элемента», а путём вычитания из элемента покомпонентных произведений, являющихся частями скалярных произведений. Поэтому следует считать вычислительным ядром метода не вычисления скалярных произведений, а вычисления выражений

$y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j}$

в режиме накопления или без него, в зависимости от требований задачи, плюс деления результатов этих вычислений на диагональные элементы матрицы.

1.1.4 Макроструктура алгоритма

Как уже записано в описании ядра алгоритма, основную часть метода обратной подстановки составляют множественные (всего $n-1$) вычисления сумм

$y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j}$

в режиме накопления или без него, плюс деления результатов этих вычислений на диагональные элементы матрицы.

1.1.5 Схема реализации последовательного алгоритма

Последовательность исполнения такова:

1. $x_{n} = y_{n}/u_{nn}$

Далее для всех $i$ от $n-1$ до $1$ по убыванию выполняются

2. $x_{i} = \left (y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j} \right ) / u_{ii}$

Особо отметим, что вычисления сумм вида $y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j}$ производят в режиме накопления вычитанием из $y_{i}$ произведений $u_{ij} x_{j}$ для $j$ от $n$ до $i + 1$, c убыванием $j$. Другие порядки выполнения суммирования приводят к резкому ухудшению параллельных свойств алгоритма, хотя, к сожалению, остаются кое-где в литературе и пакетах программ. В качестве примера такого порядка можно привести фрагмент программы из, где обратная подстановка является обратным ходом в методе Гаусса, а возрастание индекса суммирования связано, в основном, с ограничениями используемого авторами книги старого диалекта Фортрана.

1.1.6 Последовательная сложность алгоритма

Для обратной подстановки в случае решения линейной системы с верхней треугольной матрицей порядка $n$ в последовательном (наиболее быстром) варианте требуется:

• $n$ делений,
• $\frac{n^2-n}{2}$ сложений (вычитаний),
• $\frac{n^2-n}{2}$ умножений.

Умножения и сложения (вычитания) — основная часть алгоритма.

При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности (или использования функции вроде DPROD в Фортране).

При классификации по последовательной сложности, таким образом, метод обратной подстановки относится к алгоритмам со сложностью $O(n^2)$.

1.1.7 Информационный граф

Опишем граф алгоритма как аналитически, так и в виде рисунка.

Граф алгоритма обратной подстановки состоит из двух групп вершин, расположенных в целочисленных узлах двух областей разной размерности.

Рис. 1. Обратная подстановка

Первая группа вершин расположена в одномерной области, соответствующая ей операция вычисляет функцию деления. Естественно введённая единственная координата каждой из вершин $i$ меняется в диапазоне от $n$ до $1$, принимая все целочисленные значения.

Делимое в этой операции:

• при $i = n$ — элемент входных данных, а именно $y_{n}$;
• при $i \lt n$ — результат срабатывания операции, соответствующей вершине из второй группы, с координатами $i$, $i+1$.

Делитель для этой операции - элемент входных данных, а именно $u_{nn}$.

Результат срабатывания операции является выходным данным $x_{i}$.

Вторая группа вершин расположена в двумерной области, соответствующая ей операция $a-bc$. Естественно введённые координаты области таковы:

• $i$ — меняется в диапазоне от $n-1$ до $1$, принимая все целочисленные значения;
• $j$ — меняется в диапазоне от $n$ до $i+1$, принимая все целочисленные значения.

Аргументы операции следующие:

• $a$:
  • при $j = n$ элемент входных данных $y_{i}$;
  • при $j \lt n$ — результат срабатывания операции, соответствующей вершине из второй группы, с координатами $i, j+1$;
• $b$ — элемент входных данных, а именно $u_{ij}$;
• $c$ — результат срабатывания операции, соответствующей вершине из первой группы, с координатой $j$.

Результат срабатывания операции является промежуточным данным алгоритма.

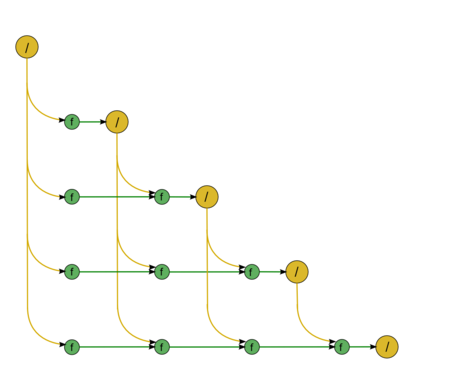
Описанный граф можно посмотреть на рис. 1, выполненном для случая $n = 5$. Здесь вершины первой группы обозначены жёлтым цветом и знаком деления, вершины второй — зелёным цветом и буквой f. Изображена подача только входных данных из вектора $y$, подача элементов матрицы $U$, идущая во все вершины, на рисунке не представлена.

1.1.8 Ресурс параллелизма алгоритма

Для обратной подстановки в случае решения линейной системы с верхней треугольной матрицей порядка $n$ в параллельном варианте требуется последовательно выполнить следующие ярусы:

• $n$ ярусов делений (в каждом из ярусов одно деление),
• по $n - 1$ ярусов умножений и сложений/вычитаний (в каждом из ярусов — линейное количество операций, от $1$ до $n-1$.

Таким образом, в параллельном варианте, в отличие от последовательного, вычисления делений будут определять довольно значительную долю требуемого времени. При реализации на конкретных архитектурах наличие в отдельных ярусах ЯПФ отдельных делений может породить и другие проблемы. Например, при реализации метода обратной подстановки на ПЛИСах остальные вычисления (умножения и сложения/вычитания) могут быть конвейеризованы, что даёт экономию и по ресурсам на программируемых платах; деления из-за их изолированности приведут к занятию ресурсов на платах, которые будут простаивать большую часть времени.

При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности, а в параллельном варианте это означает, что практически все промежуточные вычисления для выполнения алгоритма в режиме накопления должны быть двойной точности. В отличие от последовательного варианта это означает некоторое увеличение требуемой памяти.

При классификации по высоте ЯПФ, таким образом, метод обратной подстановки относится к алгоритмам с линейной сложностью. При классификации по ширине ЯПФ его сложность также будет линейной.

1.1.9 Входные и выходные данные алгоритма

Входные данные: верхняя треугольная матрица $U$ (элементы $u_{ij}$), вектор правой части $y$ (элементы $y_{i}$).

Объём входных данных: :$\frac{n (n + 3)}{2}$ (в силу треугольности достаточно хранить только ненулевые элементы матрицы $U$).

Выходные данные: вектор решения $x$ (элементы $x_{i}$).

Объём выходных данных: :$n~.$

1.1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейным (отношение квадратической к линейной).

При этом вычислительная мощность алгоритма обратной подстановки, как отношение числа операций к суммарному объему входных и выходных данных – всего лишь константа.

При этом алгоритм обратной подстановки полностью детерминирован. Использование другого порядка выполнения ассоциативных операций в данной версии нами не рассматривается, поскольку в корне меняет структуру алгоритма и меняет сложность с линейной на квадратичную.

Наличие линейного количества ярусов ЯПФ, состоящих из одного-единственного деления, потенциально замедляющее параллельные реализации алгоритма, является его характерным "узким местом", особенно в сравнении со схожей по решаемой математической задаче прямой подстановке, где диагональные элементы единичны. В связи с этим для решения СЛАУ предпочтительны такие разложения, содержащие треугольные матрицы, где в треугольных матрицах диагональные элементы единичны. В тех же случаях, когда получаются неособенные треугольные матрицы, их желательно предварительно, до решения СЛАУ с ними, преобразовать в произведение диагональной и треугольной с единичными диагональными элементами.

У алгоритма обратной подстановки существует несколько блочных вариантов. Граф некоторых из них совпадает с графом точечного варианта, различия связаны в основном с порядком прохождения основных циклов алгоритма, а именно - с их развёртыванием и перестановкой. Эти приёмы могут помочь в оптимизации обменов на конкретных вычислительных системах.