Участник:Lonalone/Генерация гауссовского вектора методом линейных преобразований
Автор описания: Меньших И. М.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
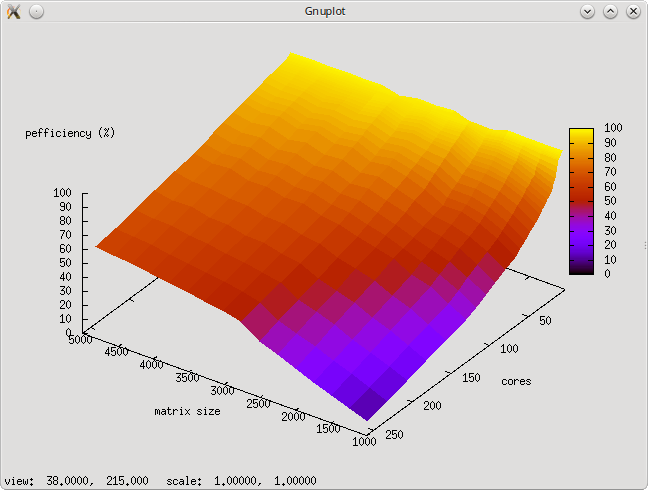
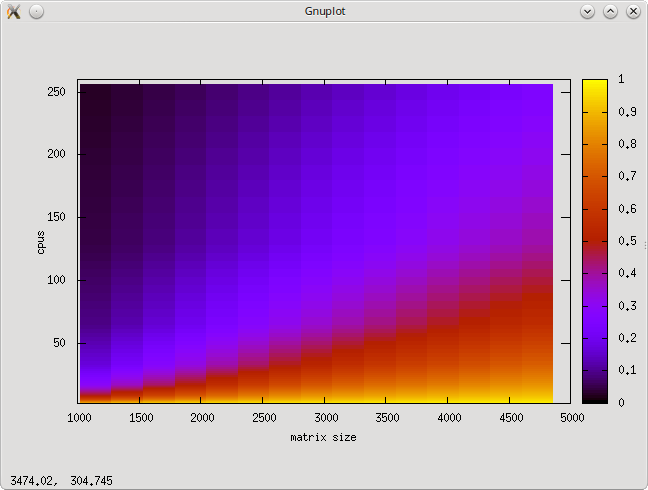
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Из многомерных распределений особый интерес представляет нормальное. Этому закону подчиняются все результаты воздействия большого числа случайных факторов, среди которых нет превалирующих.
В статье приведен алгоритм генерации n-мерного гауссовского случайного вектора с помощью метода линейных преобразований[1]. Известно, что случае нормально распределенного случайного вектора, ковариационная матрица вместе с математическим ожиданием этого вектора полностью определяют его распределение. Поэтому для полного статистического соответствия моделируемого и теоретического распределения гауссовского вектора достаточно обеспечить требуемые значения указанных параметров[2].
Идея алгоритма заключается в линейном преобразовании n-мерного случайного вектора [math]Y[/math], компоненты которого независимы и одинаково распределены по нормальному закону со стандартными параметрами, в случайный вектор [math]X[/math] с требуемыми ковариационной матрицей и вектором математических ожиданий.
1.2 Математическое описание алгоритма
1.2.1 Метод линейных преобразований
Даны ковариационная матрица [math]\Sigma[/math] и вектор математических ожиданий [math]M[/math]:
- [math] \Sigma = \|\sigma_{ij}\| = \| \mathbb{E}[(X_{i} - m_{x_{i}})(X_{j} - m_{x_{j}})]\|, \\ M = (m_{x_{1}}, m_{x_{2}}, ..., m_{x_{n}})^T. [/math]
Требуется найти такую матрицу [math]B[/math], которая позволяла бы получить искомый вектор [math]X[/math] с требуемыми характеристиками в результате линейного преобразования [math]X = BY + M[/math], где [math]Y[/math] — n-мерный случайный вектор с независимыми нормально распределенными компонентами со стандартными параметрами.
Будем искать матрицу [math]B[/math] в виде нижней треугольной матрицы. Перейдем от матричной записи к системе алгебраических уравнений:
- [math] \begin{pmatrix} X_{1} \\ X_{2} \\ \vdots \\ X_{n} \end{pmatrix} = \begin{pmatrix} b_{11} & 0 & \cdots & 0 \\b_{21} & b_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ b_{n1} & b_{n2} & \cdots & b_{nn} \end{pmatrix} \times \begin{pmatrix} Y_{1} \\ Y_{2} \\ \vdots \\ Y_{n} \end{pmatrix} + \begin{pmatrix} m_{x_{1}} \\ m_{x_{2}} \\ \vdots \\ m_{x_{n}} \end{pmatrix} \Rightarrow [/math]
- [math] \begin{cases}X_{1} - m_{x_{1}} = b_{11}Y_{1} \\X_{2} - m_{x_{2}} = b_{21}Y_{1} + b_{22}Y_{2} \\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\X_{n} - m_{x_{n}} = b_{n1}Y_{1} + b_{n2}Y_{2} + \cdots + b_{nn}Y_{n} \end{cases} [/math]
Поскольку компоненты вектора [math]Y[/math] независимы и имеют стандартные параметры, справедливо выражение:
- [math] \mathbb{E}[Y_{i}Y_{j}] = \left\{\begin{matrix} 1, &i = j, \\ 0, &i \not= j. \end{matrix}\right. [/math]
Почленно перемножив сами на себя и между собой соответственно левые и правые части уравнений системы и взяв от результатов перемножения математическое ожидание, получаем систему уравнений вида:
- [math] \begin{cases} \mathbb{E}[(X_{1} - m_{x_{1}})(X_{1} - m_{x_{1}})] = \mathbb{E}[b_{11}Y_{1}b_{11}Y_{1}], \\ \mathbb{E}[(X_{1} - m_{x_{1}})(X_{2} - m_{x_{2}})] = \mathbb{E}[(b_{21}Y_{1} + b_{22}Y_{2})b_{11}Y_{1}], \\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \end{cases} [/math]
Таким образом, в левых частях полученной системы уравнений располагаются элементы заданной ковариационной матрицы [math]\Sigma[/math], а в правых — элементы искомой матрицы [math]B[/math]. Последовательно решая эту систему, получаем формулы для расчета элементов [math]\sigma_{ij}[/math]:
- [math] b_{11}=\sqrt{\sigma_{11}}; b_{21}=\frac{\sigma_{12}}{\sqrt{\sigma_{11}}}; b_{22} = \sqrt{\sigma_{22} - \frac{\sigma_{12}}{\sigma_{11}}}, \cdots [/math]
Рекуррентная формула для расчета любого элемента матрицы преобразования [math]B[/math] имеет вид:
- [math] b_{ij} = \frac {\sigma_{ij} - \sum_{k=1}^{j-1} b_{ik} b_{jk}} {\sqrt{\sigma_{ij} - \sum_{k=1}^{j-1} b_{jk}^2}}, \quad 1 \leqslant j \leqslant i \leqslant n [/math]
(суммы с верхним нулевым пределом считаются равными нулю)
Таким образом, матрица [math]B[/math] получается с помощью разложения Холецкого матрицы [math]\Sigma[/math].
1.2.2 Генерация случайного вектора Y
Пусть имеется генератор псевдослучайных чисел (ГПСЧ, PRNG), с помощью которого можно получить реализацию случайной величины [math]u \sim U(0,1) [/math]. Описанный выше случайный вектор [math]Y=(y_1, \cdots, y_n)[/math] с независимыми компонентами составим из [math]n[/math] реализаций случайной величины [math]\eta \sim N(0,1)[/math]. Каждую такую реализацию [math]y_i[/math], в свою очередь, получим с помощью приближения по ЦПТ [math]\kappa[/math] случайными величинами, распределенными равномерно на отрезке [0,1]:
- [math] y_i = \sqrt{\frac{\kappa}{12}} (\sum_{j=1}^{\kappa}{u_j^i} - \frac{\kappa}{2}), \quad i = \overline{1, n} \\ [/math]
где [math]u_j^i - [/math] реализации случайной величины [math]u[/math], а [math]\kappa - [/math] параметр, обеспечивающий качество приближения.
Как правило, [math]\kappa[/math] берут равным 12 и считают, что для подавляющего числа практических задач обеспечивается должная точность вычислений[3].
1.3 Вычислительное ядро алгоритма
[math]\sigma_{ij} - \sum_{k=1}^{j-1} b_{ik} b_{jk}, \quad 1 \leqslant j \leqslant i \leqslant n[/math]
1.4 Макроструктура алгоритма
- Заполнение матрицы [math]B[/math]
- Генерация вектора [math]Y[/math]
- Вычисление вектора [math]X = BY + M[/math]
1.5 Схема реализации последовательного алгоритма
1) Заполнение матрицы [math]B[/math].
- (a) [math]b_{11}= \sqrt{\sigma_{11}}[/math]
- (b) [math]b_{k1}= \frac{\sigma_{k1}}{l_{11}}[/math], при [math]k = \overline{2,n}[/math]
- Следующие два пункта выполняются циклически, друг за другом для [math]i = \overline{2,n}[/math].
- (c) [math]b_{ii} = \sqrt{\sigma_{ii} - \sum_{p = 1}^{i - 1} b_{ip}^2}[/math]
- (d) [math]b_{ji} = \frac{\sigma_{ji} - \sum_{p = 1}^{i - 1} b_{ip} b_{jp}} {l_{ii}}[/math], при [math]i \neq n, j = \overline{i+1,n}[/math]
2) Генерация вектора [math]Y[/math].
- Следующие два пункта выполняются циклически, друг за другом для [math]i = \overline{1,n}[/math].
- (a) [math]u_j^i \leftarrow PRNG,[/math] при [math]j = \overline{1,k}[/math]
- (b) [math]y_i = \frac {1} {\sqrt{\frac{k}{12}} } (\sum_{j=1}^k{u_j^i} - \frac{k}{2})[/math]
3) Вычисление вектора [math]X[/math].
- [math]x_i = m_{x_i} + \sum_{k = 1}^{i} b_{ik} y_{k},[/math] при [math]i = \overline{1,n}[/math].
1.6 Последовательная сложность алгоритма
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
1.9 Входные и выходные данные алгоритма
- Входные данные: вещественная всюду плотная положительно определенная симметрическая [math](n \times n)[/math] матрица [math]\Sigma[/math] и вещественный [math](n)[/math] вектор [math]M[/math];
- Выходные данные: вещественный [math](n)[/math] вектор [math]X[/math].
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
// compute matrix B (core)
for (int j = 0; j < n; j++){
double sum_down = matrix_cov[j][j];
for (int k = 0; k < j - 1; k++){
double cur = matrix_cov[j][k];
sum_down -= cur * cur;
}
matrix_cov[j][j] = sqrt(sum_down);
for (int i = j + 1; i < n; i++){
double sum_up = matrix_cov[i][j];
for (int k = 0; k < j; k++){
sum_up -= matrix_cov[i][k] * matrix_cov[j][k];
}
matrix_cov[i][j] = sum_up / matrix_cov[j][j];
}
}
// generate vector Y
for (int i = 0; i < n; i++){
vec_Y[i] = generate_st_norm(n);
}
// linear transformation
for (int i = 0; i < n; i++){
vec_X[i] = vec_exp[i];
for (int k = 0; k <= i; k++){
vec_X[i] += matrix_cov[i][k] * vec_Y[k];
}
}
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
В отличие от разложения Холецкого, которое реализовано (точечный метод) во многих прикладных пакетах (напр., LINPACK, LAPACK, SCALAPACK), моделирование гауссовского случайного вектора не так "популярно". MS Excel и распространённые статистические пакеты (напр., SPSS, Statistica) позволяют моделировать только одномерные статистические распределения.
Имеется возможность "собрать" многомерное распределение из нескольких одномерных при условии, что компоненты независимы. Однако если необходимо исследовать данные с зависящими друг от друга переменными, то приходится писать собственную программу.
3 Литература
- ↑ (п. 1.10.4) Михайлов Г.А., Войтишек А.В. Численное статистическое моделирование. Методы Монте-Карло — М.: Академия, 2006. — 368 с.
- ↑ https://ru.wikipedia.org/wiki/Многомерное_нормальное_распределение
- ↑ Балдин К.В., Уткин В.Б. Информационные системы в экономике. — М.:Дашков и Кo, 2008. — 395 с.