Участник:Bkmish/Сортировка слиянием (последовательный и параллельный варианты)

Сортировка слиянием (MegeSort)
Текст ячейки	Текст ячейки
Текст ячейки	Текст ячейки
Текст ячейки	Текст ячейки

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Алгоритм сортировки слиянием (англ. merge sort) является методом упорядочивания списков или других структур данных, в которых доступ к элементам может быть получен только последовательно. Этот алгоритм был разработан Джоном фон Нейманом в 1945 году и является хорошим примером использования принципа «разделяй и властвуй», поскольку основан на разбиении главной задачи на более мелкие подзадачи, которые решаются, например, с помощью рекурсивного вызова или непосредственно, если количество элементов рассматриваемой структуры достаточно мало. После этого полученные результаты комбинируются для получения решения основной задачи.

1.2 Математическое описание алгоритма

В общем виде алгоритм сортировки слиянием выглядит следующим образом:

1. Разделение: исходный массив разделяется на две равные или приближенно равные части. Если массив состоит из одного элемента, он считается отсортированным. Если массив содержит более одного элемента, процесс разделения продолжается рекурсивно, пока в подмассивах не останется по одному элементу, такие подмассивы по определению считаются отсортированными.
2. Сортировка и слияние: отсортированные подмассивы сливаются в один. Процесс слияния осуществляется путем сравнения первых элементов каждого подмассива. Меньший элемент перемещается в результирующий массив, и индекс в соответствующем подмассиве увеличивается на единицу. Этот процесс продолжается, пока не будут исчерпаны все элементы в обоих подмассивах

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма сортировки слиянием − это процесс (состоящий из сравнений элементов и перемещения оставшихся элементов) слияния двух отсортированных подмассивов в один отсортированный массив. Этот процесс занимает большую часть времени работы алгоритма.

1.4 Макроструктура алгоритма

Макроструктура предложенного алгоритма сортировки слиянием состоит из двух макроопераций, соответствующих этапам алгоритма:

1. mergesort: это рекурсивная функция, которая реализует алгоритм сортировки слиянием. Она делит массив на две половины, параллельно сортирует их, а затем сливает в один отсортированный массив;
2. merge: эта функция сливает два отсортированных подмассива, полученных в результате предыдущей макрооперации, в один отсортированный массив.

1.5 Схема реализации последовательного алгоритма

Простейшая версия алгоритма сортировки слиянием может быть реализована на языке C следующим образом:

void mergesort(int a[], int i, int j) //массив a - массив для сортировки, i,j - границы области, которую нужно отсортировать
{
   int mid;
       
   if(i<j)
   {
       mid=(i+j)/2;
       mergesort(a,i,mid);     //левая рекурсия (сортировка левой половины массива)
       mergesort(a,mid+1,j);   //правая рекурсия (сортировка правой половины массива)
       }

       merge(a,i,mid,mid+1,j); //слияние двух отсортированных подмассивов
   }
}
 
void merge(int a[], int i1, int j1, int i2, int j2)
{
   int temp[1000000]; 
   int i,j,k;
   i=i1;   //начало первого подмассива
   j=i2;   //начало второго подмассива
   k=0;
   
   while(i<=j1 && j<=j2) //пока есть элементы в обоих подмассивах
   {
       if(a[i]<a[j])
           temp[k++]=a[i++];
       else
           temp[k++]=a[j++];
   }
   
   while(i<=j1)
       temp[k++]=a[i++]; //копирование оставшихся элементов 1-го подмассива
       
   while(j<=j2)
       temp[k++]=a[j++]; //копирование оставшихся элементов 2-го подмассива
       
   for(i=i1,j=0;i<=j2;i++,j++) //перенос элементов из временного в массива обратно в изначальный массив
       a[i]=temp[j];
}

Алгоритм сортировки слиянием, представленный в данном коде, работает следующим образом:

1. Рекурсивное разделение массива на подмассивы: Функция mergesort рекурсивно делит исходный массив на подмассивы, пока каждый подмассив не станет состоять из одного элемента. Это достигается путем вычисления середины массива (mid=(i+j)/2;) и разделения массива на две части: от начала до середины и от середины до конца. Затем каждая из этих частей снова рекурсивно делится до тех пор, пока не останется один элемент. Разделение на подмассивы выполняется в параллельных секциях, что позволяет ускорить процесс сортировки на многоядерных процессорах.
2. Слияние подмассивов: После того, как все подмассивы были разделены, начинается процесс слияния. Функция merge сливает два подмассива в один отсортированный массив. Это достигается путем создания временного массива temp и последовательного сравнения элементов из двух подмассивов. На каждом шаге из двух подмассивов выбирается наименьший элемент и добавляется в temp. Если в одном из подмассивов заканчиваются элементы, оставшиеся элементы из другого подмассива просто копируются в temp. Наконец, отсортированный массив temp копируется обратно в исходный массив a.
3. Исходный массив a становится полностью отсортированным.

1.6 Последовательная сложность алгоритма

Последовательная версия алгоритма сортировки слиянием имеет временную сложность [math]\Theta(n \log n)[/math] в лучшем, среднем и худшем случаях. Это происходит потому, что алгоритм разделяет массив на две половины на каждом уровне рекурсии (что требует [math]\log n[/math] уровней), а затем сливает [math]n[/math] элементов на каждом уровне, что дает общую временную сложность [math]\Theta(n \log n)[/math]

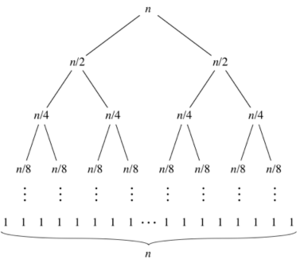
1.7 Информационный граф

Информационный граф классического алгоритма сортировки слиянием приведен на рисунке 1.

Рис.1. Информационная структура алгоритма сортировки слиянием

По мере того как подзадачи становятся меньше, количество подзадач удваивается на каждом «уровне» рекурсии, но время слияния сокращается вдвое. Удвоение и уменьшение пополам компенсируют друг друга, поэтому на каждом уровне одинаковое время объединения подмассивов. В конце концов мы переходим к подзадачам размера 1: базовому случаю. Как видно из графа, главным ресурсом параллелизма в данном алгоритме является возможность независимого выполнения рекурсивных вызовов функции mergesort() для левой и правой половин массива, поскольку эти вызовы обрабатывают разные части данных и не зависят друг от друга, что позволяет выполнять их одновременно на разных потоках.

1.8 Ресурс параллелизма алгоритма

Ресурсом параллелизма в данном алгоритме является возможность независимого выполнения рекурсивных вызовов функции mergesort() для левой и правой половин массива. Эти вызовы обрабатывают разные части данных и не зависят друг от друга, что позволяет выполнять их одновременно на разных потоках.

Параллельная версия алгоритма сортировки слиянием может быть выполнена с использованием различных подходов и, следовательно, имеет различные временные сложности. Так, используя один из алгоритмов распараллеливания, приведенный ниже в пункте 2.3, можно достичь сложности [math]\Theta(\log^2 n)[/math]

В параллельной сортировке слиянием с использованием мы распараллеливаем рекурсивные вызовы сортировки для левой и правой половин массива. Это означает, что в идеальном случае (когда количество потоков неограниченно и затраты на создание потоков и синхронизацию между ними игнорируются) оба этих вызова могут выполняться одновременно. Таким образом, максимальное время, необходимое для сортировки половин массива, будет [math]\log n[/math] (а не [math]2\log n[/math], как было бы при последовательной сортировке), что дает нам временную сложность [math]\Theta(\log n)[/math] для сортировки каждой половины массива.

После того как обе половины массива отсортированы, нам еще нужно их объединить. Этот шаг выполняется последовательно и имеет временную сложность [math]\Theta(n)[/math]. Если мы считаем, что время слияния доминирует над временем сортировки половин массива (что может быть верно для больших массивов), то общая временная сложность алгоритма будет [math]\Theta(n \log n)[/math], как и для последовательной сортировки слиянием.

Однако, если мы считаем, что время слияния не доминирует (что может быть верно для маленьких массивов), то общая временная сложность алгоритма будет [math]\Theta(\log^2 n)[/math]. Это получается из-за того, что мы делаем [math]\log n[/math] рекурсивных вызовов, и в каждом вызове мы выполняем операцию, которая требует [math]\log n[/math] времени (то есть, сортировку половины массива)

1.9 Входные и выходные данные алгоритма

Входные данные - массив чисел, который необходимо отсортировать

Выходные данные - отсортированный массив

2 Программная реализация алгоритма

2.3 Возможные способы и особенности параллельной реализации алгоритма

Вызовы mergesort() в алгоритме, представленном в пункте 1.5, обрабатывают разные части данных и не зависят друг от друга, что позволяет выполнять их одновременно на разных потоках, используя OpenMP, следующим образом:

void mergesort(int a[],int i,int j)
{
    int mid;
        
    if(i<j)
    {
        mid=(i+j)/2;
        
        #pragma omp parallel sections 
        {

            #pragma omp section
            {
                mergesort(a,i,mid);
            }

            #pragma omp section
            {
                mergesort(a,mid+1,j);
            }
        }

        merge(a,i,mid,mid+1,j);
    }
}
 
void merge(int a[],int i1,int j1,int i2,int j2)
{
    int temp[1000000];
    int i,j,k;
    i=i1;
    j=i2;
    k=0;
    
    while(i<=j1 && j<=j2)
    {
        if(a[i]<a[j])
            temp[k++]=a[i++];
        else
            temp[k++]=a[j++];
    }
    
    while(i<=j1)
        temp[k++]=a[i++];
        
    while(j<=j2)
        temp[k++]=a[j++];
        
    for(i=i1,j=0;i<=j2;i++,j++)
        a[i]=temp[j];
}

2.4 Масштабируемость алгоритма и его реализации

Масштабируемость алгоритма сортировки слиянием определяется двумя основными факторами: размером входных данных и количеством доступных потоков.

• Размер входных данных: более крупные наборы данных обычно масштабируются лучше, поскольку существует больше возможностей для параллелизма. Когда массив разбивается на подмассивы в процессе сортировки слиянием, каждый подмассив может быть обработан независимо, что позволяет выполнять эти операции параллельно. Больший размер входных данных означает больше подмассивов и, следовательно, больше возможностей для параллелизма. Однако это также означает больший объем работы для функции merge, которая выполняется последовательно и может стать узким местом для больших массивов.
• Количество доступных потоков: эффективность параллельного алгоритма также зависит от количества потоков, которые могут выполняться одновременно. Большее количество потоков позволяет обрабатывать больше подмассивов параллельно, что ускоряет общее время выполнения. Однако в реальности количество потоков, которые могут быть запущены параллельно, ограничено (обычно количеством ядер процессора), и создание потоков и синхронизация между ними также могут привести к накладным расходам, которые могут замедлить общее время выполнения.

Таким образом, алгоритм сортировки слиянием масштабируется хорошо для больших наборов данных и большого количества потоков, но его эффективность может снижаться для маленьких массивов или при ограниченных ресурсах вычислительной мощности.

2.7 Существующие реализации алгоритма

Помимо предложенного выше алгоритма, существует другая версия данного алгоритма, представленная в Introduction to Algorithms(p. 797-805). Его основная идея которого состоит в распараллеливании процесса объединения подмассивов. Ниже представлен данный алгоритм, реализованный в псевдокоде:

/**
 * A: Input array
 * B: Output array
 * lo: lower bound
 * hi: upper bound
 * off: offset
 */
algorithm parallelMergesort(A, lo, hi, B, off) is
    len := hi - lo + 1
    if len == 1 then
        B[off] := A[lo]
    else let T[1..len] be a new array
        mid := ⌊(lo + hi) / 2⌋ 
        mid' := mid - lo + 1
        fork parallelMergesort(A, lo, mid, T, 1)
        parallelMergesort(A, mid + 1, hi, T, mid' + 1) 
        join 
        parallelMerge(T, 1, mid', mid' + 1, len, B, off)

Данный алгоритм позволяет достичь временную сложность, равную [math]\Theta \left(\frac{n}{(\log n)^2}\right)[/math].

3 Литература

• Левитин А. В. Глава 4. Метод декомпозиции: Сортировка слиянием // Алгоритмы. Введение в разработку и анализ — М.: Вильямс, 2006. — С. 169—172. — 576 с. — ISBN 978-5-8459-0987-9
• Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4.
• Victor J. Duvanenko "Parallel Merge Sort" Dr. Dobb's Journal & blog
• Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. ISBN 0-262-03384-4. (p. 797-805)