Сумма вектора и произведения матрицы на другой вектор, вещественная версия, последовательный вариант, разрежённая матрица

1 Описание свойств и структуры алгоритма

1.1 Словесное описание алгоритма

Сумма вектора и произведения матрицы на другой вектор используется в качестве одной из базовых операций в широком круге методов. Здесь мы рассматриваем только вещественную арифметику, и тот вариант, когда матрица сильно разрежена.

1.2 Математическое описание

Исходные данные: два одномерных массива [math]n[/math] чисел.

Вычисляемые данные: сумма попарных произведений элементов массива.

Формулы метода: для векторов [math]\vec{x}[/math] и [math]\vec{b}[/math] размерности [math]n[/math] и [math]m[/math], соответственно, вычисляются суммы

[math]b_i = \sum_{j = 1}^n a_{ij} x_j[/math]

для всех [math]i[/math] от [math]1[/math] до [math]m[/math].

При этом в последовательном варианте используется последовательный порядок суммирования (обычно от меньших индексов к большим). Однако при работе с разрежёнными матрицами программой учитывается эта разрежённость, поэтому операции с нулевыми элементами просто не производятся. Таким образом выполняется значительное ускорение по сравнению с перемножением вектора и плотной матрицы.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро состоит из набора сумм элементов одного вектора и скалярных произведений другого на столбцы матрицы. Однако, эти скалярные произведения вычисляются не полностью, а только с участием ненулевых элементов матрицы.

1.4 Макроструктура алгоритма

Как уже записано в описании ядра алгоритма, основную часть вычисления алгоритма массовый последовательный набор сумм скалярных произведений одного вектора и столбцов матрицы с элементами одного из векторов. Однако, эти скалярные произведения вычисляются не полностью, а только с участием ненулевых элементов матрицы.

1.5 Описание схемы реализации последовательного алгоритма

Формулы метода описаны выше. Последовательность исполнения суммирования может быть разная — как по возрастанию, так и по убыванию индексов. Обычно без особых причин порядок не меняют, используя естественный (возрастание индексов), при этом суммировать начинают сразу с элементом вектора [math]\vec{b}[/math].

1.6 Последовательная сложность алгоритма

Для вычисления скалярного сумма вектора и произведения матрицы, количество операций умножения неизменно и равно [math]K[/math] (где [math]K[/math] — количество ненулевых элементов матрицы), и количество операций сложения тоже равно [math]K[/math]. Поэтому алгоритм, в случае если размеры векторов совпадают, должен быть отнесён к алгоритмам линейной сложности по количеству последовательных операций в зависимости от количества данных.

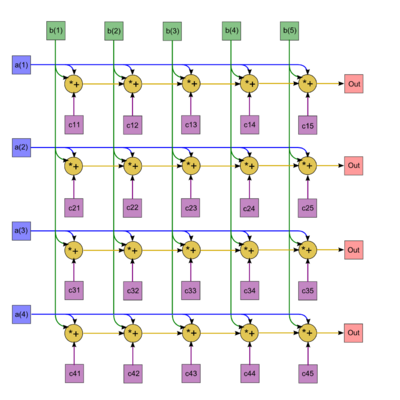
1.7 Информационный граф

Опишем граф алгоритма в виде рисунка. Пример приведён для количества ненулевых элементов в столбце, равном 7. Вершине графа соответствует составная операция умножения двух чисел с последующим сложением с третьим числом. В случае, если в столбцах разное количество ненулевых элементов, длина каждой независимой ветви вычислений будет своя, и будет равна этому количеству ненулевых элементов в соответствующем столбце.

Сумма вектора и произведения матрицы на вектор только с выходными данными

Сумма вектора и произведения матрицы на вектор с входными и выходными данными

1.8 Описание ресурса параллелизма алгоритма

Последовательный вариант вычисления суммы вектора и произведения матрицы на другой вектор, имеет ресурс параллелизма степени [math]m[/math]. Таким образом, в получившемся алгоритме высота параллельной формы будет равна [math]T[/math] операций умножения плюс [math]T[/math] операций сложения ([math]T[/math] — максимальное количество ненулевых элементов в столбце матрицы). В таком виде алгоритм, если мы предполагаем равенство размеров векторов, должен быть отнесён к алгоритмам линейной сложности по ширине параллельной формы, и к алгоритму не более, чем линейной сложности по высоте параллельной формы. Следует, однако, отметить, что при конкретной реализации выжать теоретическое быстродействие практически невозможно, поскольку структура графа оказывается зависимой от данных, а это ставит трансляторы в тупик, и те реализуют, по сути, тот же последовательный алгоритм.

1.9 Описание входных и выходных данных

Входные данные: массивы [math]\vec{x}[/math] (элементы [math]x_i[/math]), [math]\vec{b}[/math] (элементы [math]b_i[/math]), матрица [math]A[/math] (упакованные ненулевые элементы [math]a_k[/math], структурные массивы).

Дополнительные ограничения: отсутствуют.

Объём входных данных: [math]K + m + n[/math].

Выходные данные: сумма произведения матрицы [math]A[/math] и вектора [math]\vec{x}[/math] с вектором [math]\vec{b}[/math].

Объём выходных данных: [math]m[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, равно [math]m[/math]. При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — всего-навсего 2 (количество входных и выходных данных по порядку такое же, как у операций). При этом алгоритм полностью детерминирован. Дуги информационного графа локальны.

2 Программная реализация

В простейшем варианте на Фортране можно записать так:

	DO I = 1, M
	DO J = KStart(I), KFinish(I)
		B(I) = B(I) + A(J)* X(Numb(J))
	END DO
	END DO

2.7 Существующие реализации алгоритма

Помимо выписанной выше простейшей реализации, существуют более сложные коды, реализующие тот же алгоритм. Это объясняется тем, что разные разрежённые матрицы удобно хранить по-разному.