Участник:KibAndrey/Ортогонализация Грама-Шмидта

Ортогонализация Грама-Шмидта
Последовательный алгоритм
Последовательная сложность	$O\left(n^3\right)$
Объём входных данных
Объём выходных данных
Параллельный алгоритм
Высота ярусно-параллельной формы
Ширина ярусно-параллельной формы

Основные авторы описания: А.В.Кибанов, Т.З.Аджиева.

1 ЧАСТЬ. Свойства и структура алгоритма

1.5 Информационный граф

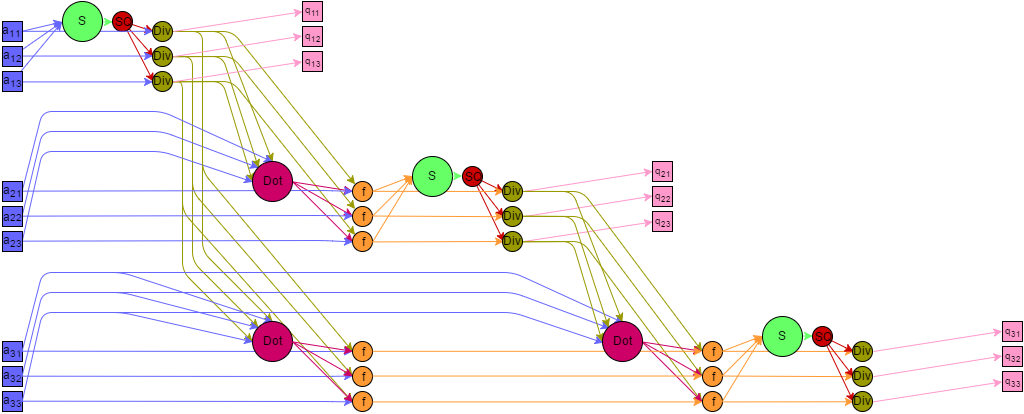
Представим граф алгоритма с помощью текстового описания, а также с помощью изображения.

Все вершины графа можно разбить на шесть групп, каждой из которых соответствует вид исполняемой операции. Каждая вершина расположена в точках с целочисленными координатами, в пространствах с числом измерений от $1$ до $4$ Дадим описание каждой из групп.

Первая группа - вершины, которым соответствует операция возведение в квадрат. На графе они располагаются в двумерной области. $i$ изменяется от $1$ до $n$, $k$ изменяется от $1$ до $m$.

Значениями аргументов для этих функций являются:

• при $i = 1$ - входные данные $a_{1k}$;
• при $i \gt 1$ - результат выполнения функции в вершине шестой группы с координатами $i-1,1,k$

Результат является промежуточным данным алгоритма.

Вторая группа - вершины соответствующие операции сложения, которые проще разбить на две подгруппы, соответствующие четным и нечетным индексам. Они располагаются в четырехмерной области, $i$ изменяется от $1$ до $2n-1$, $j$ равно $1$ для нечетных $i$ и изменяется от $2$ до $n+1-\lceil{\dfrac{i}{2}}\rceil$ для четных $i$, $k$ изменяется от $1$ до $\lceil{\dfrac{m}{2^{i}}}\rceil$, $t$ изменяется от $1$ до $T = \lceil{\log_{2}(k)}\rceil+1$.

Значениями аргументов для этих функций являются:

• при $j = 1, t = 1$ - результат выполнения функций в вершинах первой группы с координатами $(i+1)/2,1,2*k$ и $(i+1)/2,1,2*k - 1$ ;
• при $j \gt 1, t = 1$ - результат выполнения функции в вершинах пятой группы с координатами $i/2,j-1,2*k$ и $i,j-1,2*k - 1$;
• при $t \gt 1$ - результат выполнения функций в вершинах второй группы с координатами $i,j,2*k,t-1$ и $i,j,2*k-1,t-1$ (это точно верно для случаев k являющихся степенью двойки. Для остальных вариантов аргументом может являться результат выполнения функций в вершинах второй группы с последней координатой меньшей чем $t-1$).

Результат является промежуточным данным алгоритма.

Третья группа - вершины, которым соответствует операция SQRT извлечения квадратного корня. Они расположены в одномерной области, $i$изменяется от $1$ до $n$. Значением аргумента для этих функций является результат выполнения функции в вершине второй группы, с координатами $i,1,1,T$

Результат является промежуточным данным алгоритма

Четвертая группа - вершины, которым соответствует операция деления. Располагаются в двумерной области, $i$ изменяется от $1$ до $n$, $k$ изменяется от $1$ до $m$. Значениями аргументов для этих функций являются:

• делимое:
  • при $i = 1$ - входные данные $a_{1k}$;
  • при $i \gt 1$ - результат выполнения функции в вершине шестой группы с координатами $i-1,1,k$;
• делитель - результат выполнения функции в вершине третьей группы с координатой $i$

Результат является выходным данным алгоритма $e_{ik}$

Пятая группа - вершины, которым соответствует операция $a*b$. Располагаются в трехмерной области, $i$ изменяется от $1$ до $n-1$, $j$ изменяется от $1$ до $n-i\lt math\gt , \lt math\gt k$ изменяется от $1$ до $m$. Значениями аргументов для этих функций являются:

• $a$:
  • при $i = 1$ - входные данные $a_{1+j,k}$;
  • при $i \gt 1$ - результат выполнения функции в вершине шестой группы с координатами $i-1,j+1,k$;
• $b$ - результат выполнения функции в вершине четвертой группы с координатой $i$

Результат является промежуточным данным алгоритма

Шестая группа - вершины которые соответствуют операции $a - b*c$. Располагаются в трехмерной области, $i$ изменяется от $1$ до $n-1$, $j$ изменяется от $1$ до $n-i$, $k$ изменяется от $1$ до $m$. Значениями аргументов для этих функций являются:

• $a$:
  • при $i = 1$ - входные данные $a_{1+j,k}$;
  • при $i \gt 1$ - результат выполнения функции в вершине шестой группы с координатами $i-1,j+1,k$;
• $b$ - результат выполнения функции в вершине второй группы, с координатами $i,j+1,1,T$
• $c$ - результат выполнения функции в вершине четвертой группы с координатой $i$

Результат является промежуточным данным алгоритма

Описанный граф для случая $n = 3$, $k = 4$ изображен на рисунке. Каждая группа вершин отличается цветом и буквенным обозначением. "S" - первая группа, "+" - вторая группа, "SQ" - третья группа, "Div" - четвертая группа, "M" - пятая группа, "f" - шестая группа. Квадратные метки "In" и "out" обозначают передачу входных и выходных данных соответственно. Поскольку координаты вдоль оси $k$ в большинстве случаев соответствуют номеру компоненты рассматриваемого вектора, для удобства визуализации изменение этой координаты зафиксировано локально в каждой подгруппе вершин с одинаковыми координатами $i,j$ параллельно оси $j$.

Рисунок 1. Граф алгоритма с отображением входных и выходных данных

1.6 Ресурс параллелизма алгоритма

Для построения ортонормированного базиса методом Грама-Шмидта необходимо выполнить следующие ярусы операций:

• $n$ ярусов вычисления квадратов числа (по $k$ операций на каждом)
• $(2n-1)*(\lceil{\log_{2}(k)}\rceil+1)$ ярусов суммирования (от $1$ до $(n-1)*\dfrac{k}{2}$ операций на каждом)
• $n$ ярусов вычисления квадратного корня (по одной операции на каждом)
• $n$ ярусов деления( по $k$ операций на каждом)
• $n-1$ ярус умножения пары чисел (от $1$ до $k*(n-1)$ операций на каждом)
• $n-1$ ярус умножения/вычитания чисел (от $k$ до $k*(n-1)$ операций на каждом)

В этом случае сложность алгоритма при классификации по высоте ЯПФ - $O(n\log{k})$, при классификации по ширине ЯПФ - $O(n*k)$

1.7 Входные и выходные данные алгоритма

Входные данные: Невырожденная матрица $A$(с элементами $a_{ij}$), по строкам которой записаны $n$ векторов некоторого пространства размерности $k$.

Объем входных данных:$nk$.

Выходные данные: Матрица $B_e$(с элементами $e_{ij}$). Строки этой матрицы также задают вектора, такие, что длина каждого вектора равна единицы, а скалярное произведение двух различных векторов равно $0$.

Объем выходных данных: $nk$

Замечание: Алгоритм может работать с вырожденной матрицей, он выдаёт нулевую строку на шаге $j$, если строка $j$ матрицы $A$ является линейной комбинацией предыдущих строк. В этом случае для корректного продолжения работы алгоритма необходима дополнительная проверка на равенство строки нулю и пропуск соответствующих строк. Количество построенных векторов будет равняться размерности пространства, порождаемого строками матрицы.