Уровень алгоритма

Участник:KibAndrey/Ортогонализация Грама-Шмидта

Материал из Алговики
Перейти к навигации Перейти к поиску


Ортогонализация Грама-Шмидта
Последовательный алгоритм
Последовательная сложность [math]O\left(n^3\right)[/math]
Объём входных данных [math]kn[/math]
Объём выходных данных [math]kn[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы [math]O(n\log{k})[/math]
Ширина ярусно-параллельной формы [math]O(kn)[/math]


Основные авторы описания: А.В.Кибанов, Т.З.Аджиева.



1 ЧАСТЬ. Свойства и структура алгоритма

1.1 Общее описание алгоритма

Процесс ортогонализации Грама–Шмидта[1] — алгоритм построения для данной линейно независимой системы векторов евклидова или эрмитова пространства [math]V[/math] ортогональной системы ненулевых векторов, которые имеют ту же самую линейную оболочку, при котором каждый вектор построенной системы линейно выражается через векторы данной системы. Исторически это первый алгоритм, описывающий процесс ортогониализации. Традиционно его связывают с именами Йоргена Педерсена Грама и Эрхарда Шмидта. Йорган Педерсен Грам[2] был датским актуарием, который в неявном виде представил суть процесса ортогонализации в 1883 году. Ясно, что Грам не знал о том, что Лаплас ранее использовал этот метод. Эрхард Шмидт[2] был учеником великих математиков Германа Шварца и Давида Гильберта. Алгоритм ортогонализации был опубликован Э. Шмидтом в 1907 году [3] в его исследовании интегральных уравнений, которое в свою очередь дало привело к развитию теории гильбертовых пространств. Шмидт использовал процесс ортогонализации применительно к геометрии гильбертова пространства решений интегральных уравнений отмечал, что процесс ортогонализации принципиально такой же, какой прежде использовал Й. Грам. В отечественной литературе иногда этот процесс называют "ортогонализацией Сонина–Шмидта"[4][5]. Это название связано с тем, что разработанный Сониным [6] метод ортогонализации системы функций для частного случая по существу не отличается от метода ортогонализации системы функций, предложенного ранее Шмидтом[3].

1.2 Математическое описание алгоритма

Bходные данные: [math]k[/math] линейно независимых векторов [math]\mathbf{a_1},\mathbf{a_2},\ldots,\mathbf{a_k}[/math] длины [math]n[/math] [math]\left(\alpha_{ij}\right.[/math], [math]j=1,2, \ldots,n[/math], — координаты вектора [math]\left.\mathbf{a_i}\right)[/math] .

Вычисляемые данные:

[math]k[/math] ортогональных векторов [math]\mathbf{b_1},\mathbf{b_2},...,\mathbf{b_k}[/math] длины [math]n[/math], причем [math]\mathbf{b_1}=\mathbf{a_1}[/math] либо

[math]k[/math] ортонормированных векторов [math]\mathbf{e_1},\mathbf{e_2},\ldots,\mathbf{e_k}[/math] длины [math]n[/math], причем [math]\mathbf{e_i}=\frac{\mathbf{a_i}}{|\mathbf{a_i}|}[/math], [math]i=1,2, \ldots,k[/math]

Формулы процесса ортогонализации:

[math] \begin{align} \mathbf{b_{1}} & =\mathbf{a_{1}}, \\ \mathbf{b_{2}}& =\mathbf{a_{2}}-proj_{\mathbf{b_1}}\mathbf{a_{1}}, \\ & ...\\ \mathbf{b_{{i} }} & = \mathbf{a_{i}}-\sum\limits_{j=1}^{i-1} proj_{\mathbf{b_j}}\mathbf{a_{i}},\\ & ...\\ \mathbf{b_{k}} & =\mathbf{ a_{k}}-\sum\limits_{j=1}^{k-1} proj_{\mathbf{b_j}}\mathbf{a_{k}},\\ \end{align} [/math]

Здесь [math]proj_{\mathbf{b_j}}\mathbf{a_{i}}[/math], для [math]j=1,...,i-1[/math] — проекция вектора [math]\mathbf{a_{i}}[/math] на направление вектора [math]\mathbf{b_{j}}[/math]. Это число, равное по величине проекции вектора [math]\mathbf{a_{j}}[/math] на ось, проходящую через вектор [math]\mathbf{b_j}[/math].

Формула для ее вычисления, полученная из определения скалярного произведения: [math]proj_{\mathbf{b_j}}\mathbf{a_{i}}=\dfrac{(ai,bj)}{\mathbf{\left \|b_j\right \|}}[/math], для [math]j=1,...,i-1[/math]

В этом случае знаменатель в формуле для вычисления проекции [math]|\mathbf{e_i}|=1[/math] для [math]i=1,...,k-1[/math], что существенно упрощает вычисления алгоритма.

Произведение длин [math]\mathbf{|b_1|},\mathbf{|b_2|},\ldots ,\mathbf{|b_k|}[/math] равно объему параллелепипеда, построенного на векторах системы [math]\left\{\mathbf{a_i}\right\}[/math], [math]i=1,2,\ldots ,k[/math], как на ребрах

Явное выражение векторов [math]\mathbf{b_i}[/math] для [math]i=1,...,k[/math] через [math]\mathbf{a_1},\mathbf{a_2},...,\mathbf{a_k}[/math] дает формула

[math] \mathbf{b_i}= \begin{vmatrix} (a_1,a_1) & \cdots & (a_1,a_k-1) &a_1 \\ \cdots & \cdots & \cdots & \cdots \\ (a_{i},a_1) & \cdots & (a_i,a_k-1) &a_i \\ \cdots & \cdots & \cdots& \cdots \\ (a_{k},a_1) & \cdots & (a_k,a_k-1) &a_k \end{vmatrix} [/math]. (В правой части этого равенства определитель следует формально разложить по последнему столбцу).

Иногда полученные векторы нормируются сразу после их нахождения и находится система ортонормированных векторов [math]\mathbf{e_1},\mathbf{e_2},\ldots,\mathbf{e_k}[/math]. В этом случае знаменатель в формуле для вычисления проекции [math]|\mathbf{e_i}|=1[/math] для [math]i=1,...,k-1[/math], что существенно упрощает вычисления алгоритма.

1.3 Макроструктура алгоритма

1.4 Схема реализации последовательного алгоритма

Входные данные: [math]k[/math] линейно независимых векторов [math]\mathbf{a_1},\mathbf{a_2},\ldots,\mathbf{a_k}[/math] длины [math]n[/math] (координаты вектора [math]\mathbf{a_i}[/math] для [math]i=1,2, \ldots,k[/math] — [math]\alpha_{ij}[/math], [math]j=1,2, \ldots,n[/math]) .

Вычисляемые данные:

[math]k[/math] ортогональных векторов [math]\mathbf{b_1},\mathbf{b_2},...,\mathbf{b_k}[/math] длины [math]n[/math], причем [math]\mathbf{b_1}=\mathbf{a_1}[/math] ([math]\left(\beta_{ij}\right.[/math], [math]j=1,2, \ldots,n[/math], — координаты вектора [math]\left.\mathbf{b_i}\right)[/math] для [math]i=1,2, \ldots,k[/math]). либо

[math]k[/math] ортонормированных векторов [math]\mathbf{e_1},\mathbf{e_2},\ldots,\mathbf{e_k}[/math] длины [math]n[/math], причем [math]\mathbf{e_i}=\frac{\mathbf{a_i}}{|\mathbf{a_i}|}[/math], для [math]i=1,2, \ldots,k[/math]


Последовательность исполнения метода следующая: 1. Q = A; for k = 1 : n for i = 1 : k − 1; R(i, k) = Q(:, i) 0 ∗ Q(:, k); end (Omit this line for CMGS) for i = 1 : k − 1, (Omit this line for CMGS) Q(:, k) = Q(:, k) − R(i, k) ∗ Q(:, i); end R(k, k) = norm(Q(:, k)); Q(:, k) = Q(:, k)/R(k, k); end

1.5 Вычислительное ядро алгоритма

1.6 Последовательная сложность алгоритма

Для ортогонализации [math]n[/math] линейно независимых векторов длины [math]n[/math] в последовательном варианте с помощью классического метода ортогонализации Грама-Шмидта потребуется:

  • [math]k[/math] вычислений квадратного корня
  • [math]\frac{k(k-1)(n-1)}{2}[/math] сложений,
  • [math]\frac{k(k-1)(n-1)}{2}[/math] вычитаний,
  • [math]k^2 n[/math] умножений,
  • [math]k[/math] делений.

Умножения, сложения и вычитания составляют основную часть алгоритма.

При классификации по последовательной сложности, таким образом, метода ортогонализации Грама-Шмидта с кубической сложностью.

1.7 Информационный граф

Представим граф алгоритма с помощью текстового описания, а также с помощью изображения.

Все вершины графа можно разбить на шесть групп, каждой из которых соответствует вид исполняемой операции. Каждая вершина расположена в точках с целочисленными координатами, в пространствах с числом измерений от [math]1[/math] до [math]4[/math] Дадим описание каждой из групп.

Первая группа — вершины, которым соответствует операция возведение в квадрат. На графе они располагаются в двумерной области. [math]i[/math] изменяется от [math]1[/math] до [math]n[/math], [math]k[/math] изменяется от [math]1[/math] до [math]m[/math].

Значениями аргументов для этих функций являются:

  • при [math]i = 1[/math] — входные данные [math]\alpha_{1k}[/math];
  • при [math]i \gt 1[/math] — результат выполнения функции в вершине шестой группы с координатами [math]i-1,1,k[/math]

Результат является промежуточным данным алгоритма.

Вторая группа - вершины соответствующие операции сложения, которые проще разбить на две подгруппы, соответствующие четным и нечетным индексам. Они располагаются в четырехмерной области, [math]i[/math] изменяется от [math]1[/math] до [math]2n-1[/math], [math]j[/math] равно [math]1[/math] для нечетных [math]i[/math] и изменяется от [math]2[/math] до [math]n+1-\left\lceil{\dfrac{i}{2}}\right\rceil[/math] для четных [math]i[/math], [math]k[/math] изменяется от [math]1[/math] до [math]\left\lceil{\dfrac{m}{2^{i}}}\right\rceil[/math], [math]t[/math] изменяется от [math]1[/math] до [math]T = \left\lceil{\log_{2}(k)}\right\rceil+1[/math].

Значениями аргументов для этих функций являются:

  • при [math]j = 1, t = 1[/math] – результат выполнения функций в вершинах первой группы с координатами [math](i+1)/2,1,2*k[/math] и [math](i+1)/2,1,2*k - 1[/math];
  • при [math]j \gt 1, t = 1[/math] – результат выполнения функции в вершинах пятой группы с координатами [math]i/2,j-1,2*k[/math] и [math]i,j-1,2*k - 1[/math];
  • при [math]t \gt 1[/math] – результат выполнения функций в вершинах второй группы с координатами [math]i,j,2*k,t-1[/math] и [math]i,j,2*k-1,t-1[/math] (это точно верно для случаев k являющихся степенью двойки. Для остальных вариантов аргументом может являться результат выполнения функций в вершинах второй группы с последней координатой меньшей чем [math]t-1[/math]).

Результат является промежуточным данным алгоритма.

Третья группа – вершины, которым соответствует операция SQRT извлечения квадратного корня. Они расположены в одномерной области, [math]i [/math]изменяется от [math]1[/math] до [math]n[/math]. Значением аргумента для этих функций является результат выполнения функции в вершине второй группы, с координатами [math]i,1,1,T[/math]

Результат является промежуточным данным алгоритма

Четвертая группа – вершины, которым соответствует операция деления. Располагаются в двумерной области, [math]i[/math] изменяется от [math]1[/math] до [math]n[/math], [math]k[/math] изменяется от [math]1[/math] до [math]m[/math]. Значениями аргументов для этих функций являются:

  • делимое:
    • при [math]i = 1[/math] – входные данные [math]a_{1k}[/math];
    • при [math]i \gt 1[/math] – результат выполнения функции в вершине шестой группы с координатами [math]i-1,1,k[/math];
  • делитель - результат выполнения функции в вершине третьей группы с координатой [math]i[/math]

Результат является выходным данным алгоритма [math]e_{ik}[/math]

Пятая группа – вершины, которым соответствует операция [math]a*b[/math]. Располагаются в трехмерной области, [math]i[/math] изменяется от [math]1[/math] до [math]n-1[/math], [math]j[/math] изменяется от [math]1[/math] до [math]n-i[/math], [math]k[/math] изменяется от [math]1[/math] до [math]m[/math]. Значениями аргументов для этих функций являются:

  • [math]a[/math]:
    • при [math]i = 1[/math] – входные данные [math]a_{1+j,k}[/math];
    • при [math]i \gt 1[/math] – результат выполнения функции в вершине шестой группы с координатами [math]i-1,j+1,k[/math];
  • [math]b[/math] – результат выполнения функции в вершине четвертой группы с координатой [math]i[/math]

Результат является промежуточным данным алгоритма

Шестая группа – вершины которые соответствуют операции [math]a - b*c[/math]. Располагаются в трехмерной области, [math]i[/math] изменяется от [math]1[/math] до [math]n-1[/math], [math]j[/math] изменяется от [math]1[/math] до [math]n-i[/math], [math]k[/math] изменяется от [math]1[/math] до [math]m[/math]. Значениями аргументов для этих функций являются:

  • [math]a[/math]:
    • при [math]i = 1[/math] – входные данные [math]a_{1+j,k}[/math];
    • при [math]i \gt 1[/math] – результат выполнения функции в вершине шестой группы с координатами [math]i-1,j+1,k[/math];
  • [math]b[/math] – результат выполнения функции в вершине второй группы, с координатами [math]i,j+1,1,T[/math]
  • [math]c[/math] – результат выполнения функции в вершине четвертой группы с координатой [math]i[/math]

Результат является промежуточным данным алгоритма.

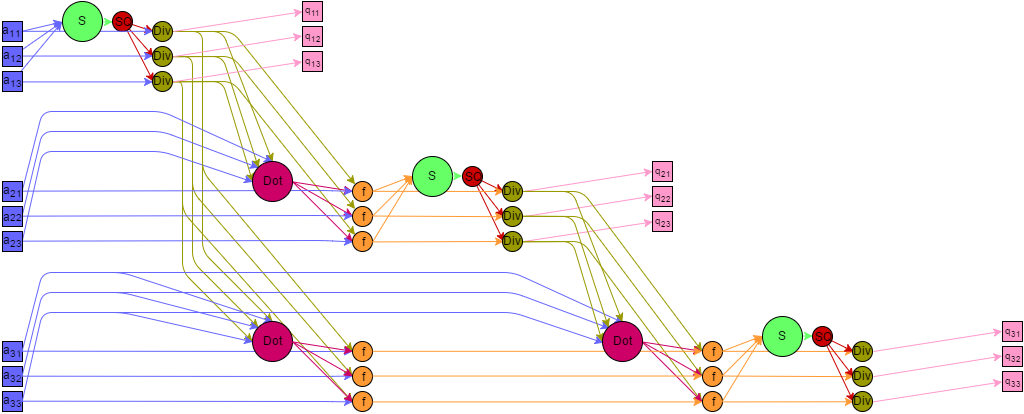
Описанный граф для случая [math]n = 3[/math], [math]k = 4[/math] изображен на рисунке. Каждая группа вершин отличается цветом и буквенным обозначением. "S" – первая группа, "+" – вторая группа, "SQ" – третья группа, "Div" – четвертая группа, "M" – пятая группа, "f" – шестая группа. Квадратные метки "In" и "out" обозначают передачу входных и выходных данных соответственно. Поскольку координаты вдоль оси [math]k[/math] в большинстве случаев соответствуют номеру компоненты рассматриваемого вектора, для удобства визуализации изменение этой координаты зафиксировано локально в каждой подгруппе вершин с одинаковыми координатами [math]i,j[/math] параллельно оси [math]j[/math].

Рисунок 1. Граф алгоритма с отображением входных и выходных данных


https://algowiki-project.org/algowiki/pool/images/f/f9/Orthogonalization_1.png

1.8 Ресурс параллелизма алгоритма

Для построения ортонормированного базиса методом Грама–Шмидта необходимо выполнить следующие ярусы операций:

  • [math]n[/math] ярусов вычисления квадратов числа (по [math]k[/math] операций на каждом)
  • [math](2n-1)*\left(\left\lceil{\log_{2}(k)}\right\rceil+1\right)[/math] ярусов суммирования (от [math]1[/math] до [math](n-1)*\dfrac{k}{2}[/math] операций на каждом)
  • [math]n[/math] ярусов вычисления квадратного корня (по одной операции на каждом)
  • [math]n[/math] ярусов деления( по [math]k[/math] операций на каждом)
  • [math]n-1[/math] ярус умножения пары чисел (от [math]1[/math] до [math]k*(n-1)[/math] операций на каждом)
  • [math]n-1[/math] ярус умножения/вычитания чисел (от [math]k[/math] до [math]k*(n-1)[/math] операций на каждом)

В этом случае сложность алгоритма при классификации по высоте ЯПФ — [math]O(n\log{k})[/math], при классификации по ширине ЯПФ — [math]O(n*k)[/math]

1.9 Входные и выходные данные алгоритма

Входные данные: Невырожденная матрица [math]A[/math] с элементами [math]a_{ij}[/math]. По строкам этой матрицы записаны [math]k[/math] векторов некоторого пространства размерности [math]n[/math].

Объем входных данных: [math]kn[/math].

Выходные данные: Матрица [math]B_e[/math] с элементами [math]\varepsilon_{ij}[/math]. Строки этой матрицы также задают вектора, такие, что длина каждого вектора равна единицы, а скалярное произведение двух различных векторов равно [math]0[/math].

Объем выходных данных: [math]kn[/math]

Замечание: Алгоритм может работать с вырожденной матрицей, он выдаёт нулевую строку на шаге [math]j[/math], если строка [math]j[/math] матрицы [math]A[/math] является линейной комбинацией предыдущих строк. В этом случае для корректного продолжения работы алгоритма необходима дополнительная проверка на равенство строки нулю и пропуск соответствующих строк. Количество построенных векторов будет равняться размерности пространства, порождаемого строками матрицы.

1.10 Свойства алгоритма

2 ЧАСТЬ Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

Срок сдачи продлён до 15-го ноября.

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

3 Литература

  1. ↑ Математическая энциклопедия / Гл. ред. И. М. Виноградов — М: Советская энциклопедия — Т.4 Ок–Сло, 1984. — 215 с.
  2. ↑ 2,0 2,1 Meyer C. D. Matrix analysis and applied linear algebra. — Siam, 2000. — Т.2.
  3. ↑ 3,0 3,1 Erchard Shmidt. Mathematische Annalen Zur Theorie der linearen und nichtlinearen Integralgleichungen, 1. Teil: Entwicklung willkürlicher Funktionen nach Systemen vorgeschriebener. – Mathematische Annalen, 63 (1907), pp. 433–476. Ошибка цитирования Неверный тег <ref>: название «Shmidt» определено несколько раз для различного содержимого
  4. ↑ Краснов М.Л. Интегральные уравнения. Введение в теорию. — М.: Наука, 1975. — 302 с.
  5. ↑ Марченко В.А. Введение в теорию обратных задач спектрального анализа. — Харьков: Акта, 2005. — 143 с.
  6. ↑ О некоторых неравенствах, относящихся к определенным интегралам. Записки Академии наук по физико-математическому отделению. Серия 8. Т. 6 № 6. — C. 1–53.
Источник — https://algowiki-project.org/w/ru/index.php?title=Участник:KibAndrey/Ортогонализация_Грама-Шмидта&oldid=8709