Обратная подстановка (вещественный вариант)

1 Описание свойств и структуры алгоритма

1.1 Словесное описание алгоритма

Обратный ход метода Гаусса, или обратная подстановка - решение СЛАУ [math]Ux = y[/math] с правой треугольной матрицей [math]U[/math]. Матрица [math]U[/math] - одна из составляющих матрицы [math]A[/math] и получается либо из [math]LU[/math]-разложения последней каким-либо из многочисленных способов (например, простое разложение Гаусса, разложение Гаусса с выбором ведущего элемента, компактная схема Гаусса, разложение Холецкого и др.), либо из других разложений. В силу треугольности [math]U[/math] решение СЛАУ является одной из модификаций общего метода подстановки и записывается простыми формулами.

В [1] методом обратной подстановки назван также и метод решения СЛАУ с левой треугольной матрицей. Там же отмечено, что в литературе иногда под обратной подстановкой имеют в виду, как и здесь, только решения СЛАУ с правой треугольной матрицей, а решение левых треугольных систем называют прямой подстановкой. Такой же системы названий будем придерживаться и мы, во избежание одноимённого названия разных алгоритмов. Кроме того, обратная подстановка, представленная здесь, одновременно является частью метода Гаусса для решения СЛАУ, а именно - его обратным ходом, чего нельзя сказать про прямую подстановку.

1.2 Математическое описание

Исходные данные: правая треугольная матрица [math]U[/math] (элементы [math]u_{ij}[/math]), вектор правой части [math]y[/math] (элементы [math]y_{i}[/math]).

Вычисляемые данные: вектор решения [math]x[/math] (элементы [math]x_{i}[/math]).

Формулы метода:

[math] \begin{align} x_{n} & = y_{n}/u_{nn} \\ x_{i} & = \left (y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j} \right ) / u_{ii}, \quad i \in [1, n - 1]. \end{align} [/math]

Существует также блочная версия метода, однако в данном описании разобран только точечный метод.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро обратной подстановки можно составить из множественных (всего их [math]n-1[/math]) вычислений скалярных произведений строк матрицы [math]U[/math] на уже вычисленную часть вектора [math]x[/math]:

[math] \sum_{j = i+1}^{n} u_{ij} x_{j} [/math]

в режиме накопления или без него, в зависимости от требований задачи, с их последующим вычитанием из компоненты вектора [math]y[/math] и деления на диагональный элемент матрицы [math]U[/math]. В отечественных реализациях, даже в последовательных, упомянутый способ представления не используется. Дело в том, что даже в этих реализациях метода вычисление сумм типа

[math] y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j} [/math]

в которых и встречаются скалярные произведения, ведутся не в порядке «вычислили скалярное произведение, а потом вычли его из элемента», а путём вычитания из элемента покомпонентных произведений, являющихся частями скалярных произведений. Поэтому следует считать вычислительным ядром метода не вычисления скалярных произведений, а вычисления выражений

[math] y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j} [/math]

в режиме накопления или без него, в зависимости от требований задачи, плюс деления результатов этих вычислений на диагональные элементы матрицы.

1.4 Макроструктура алгоритма

Как уже записано в описании ядра алгоритма, основную часть метода обратной подстановки составляют множественные (всего [math]n-1[/math]) вычисления сумм

[math]y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j} [/math]

в режиме накопления или без него, плюс деления результатов этих вычислений на диагональные элементы матрицы.

1.5 Описание схемы реализации последовательного алгоритма

Чтобы понять последовательность исполнения, перепишем формулы метода так:

1. [math]x_{n} = y_{n}/u_{nn}[/math]

Далее для всех [math]i[/math] от [math]n-1[/math] до [math]1[/math] по убыванию выполняются

2. [math]x_{i} = \left (y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j} \right ) / u_{ii}[/math]

Особо отметим, что вычисления сумм вида [math]y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j}[/math] производят в режиме накопления вычитанием из [math]y_{i}[/math] произведений [math]u_{ij} x_{j}[/math] для [math]j[/math] от [math]n[/math] до [math]i + 1[/math], c убыванием [math]j[/math]. Другие порядки выполнения суммирования приводят к резкому ухудшению параллельных свойств алгоритма, хотя, к сожалению, остаются кое-где в литературе и пакетах программ.В качестве примера такого порядка можно привести фрагмент программы из [2], где обратная подстановка является обратным ходом в методе Гаусса, а возрастание индекса суммирования связано, в основном, с ограничениями старого диалекта Фортрана.

1.6 Последовательная сложность алгоритма

Для обратной подстановки порядка n в последовательном (наиболее быстром) варианте требуется:

• [math]n[/math] делений,
• по [math]\frac{n^2-n}{2}[/math] умножений и сложений (вычитаний) — основная часть алгоритма.

При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности (или использования функции вроде DPROD в Фортране), что ещё больше увеличивает долю умножений и сложений/вычитаний во времени, требуемом для выполнения обратного хода метода Гаусса.

При классификации по последовательной сложности, таким образом, метод обратной подстановки относится к алгоритмам с квадратической сложностью.

1.7 Информационный граф

Опишем граф алгоритма как аналитически, так и в виде рисунка.

Граф алгоритма обратной подстановки состоит из двух групп вершин, расположенных в целочисленных узлах двух областей разной размерности.

Обратная подстановка

Первая группа вершин расположена в одномерной области, соответствующая ей операция вычисляет функцию деления. Естественно введённая единственная координата каждой из вершин [math]i[/math] меняется в диапазоне от [math]n[/math] до [math]1[/math], принимая все целочисленные значения.

Делимое в этой операции:

• при [math]i = n[/math] — элемент входных данных, а именно [math]y_{n}[/math];
• при [math]i \lt n[/math] — результат срабатывания операции, соответствующей вершине из второй группы, с координатами [math]i[/math], [math]i+1[/math].

Делитель для этой операции - элемент входных данных, а именно [math]u_{nn}[/math].

Результат срабатывания операции является выходным данным [math]x_{i}[/math].

Вторая группа вершин расположена в двумерной области, соответствующая ей операция [math]a-bc[/math]. Естественно введённые координаты области таковы:

• [math]i[/math] — меняется в диапазоне от [math]n-1[/math] до [math]1[/math], принимая все целочисленные значения;
• [math]j[/math] — меняется в диапазоне от [math]n[/math] до [math]i+1[/math], принимая все целочисленные значения.

Аргументы операции следующие:

• [math]a[/math]:
  • при [math]j = n[/math] элемент входных данных [math]y_{i}[/math];
  • при [math]j \lt n[/math] — результат срабатывания операции, соответствующей вершине из второй группы, с координатами [math]i, j+1[/math];
• [math]b[/math] — элемент входных данных, а именно [math]u_{ij}[/math];
• [math]c[/math] — результат срабатывания операции, соответствующей вершине из первой группы, с координатой [math]j[/math];

Результат срабатывания операции является промежуточным данным алгоритма.

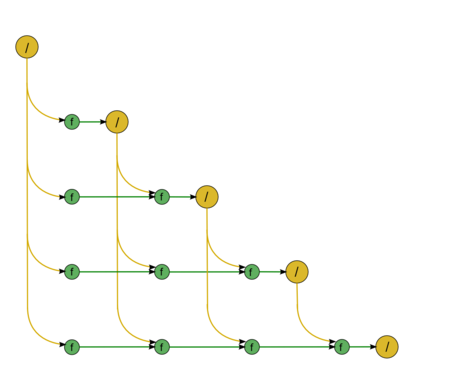
Описанный граф можно посмотреть на рисунке, выполненном для случая [math]n = 5[/math]. Здесь вершины первой группы обозначены ;`жёлтым цветом и знаком деления, вершины второй — зелёным цветом и буквой f. Изображена подача только входных данных из вектора [math]y[/math], подача элементов матрицы [math]U[/math], идущая во все вершины, на рисунке не представлена.

1.8 Описание ресурса параллелизма алгоритма

Для обратной подстановки порядка n в параллельном варианте требуется последовательно выполнить следующие ярусы:

• [math]n[/math] ярусов делений (в каждом из ярусов одно деление),
• по [math]n - 1[/math] ярусов умножений и сложений/вычитаний (в каждом из ярусов — линейное количество операций, от [math]1[/math] до [math]n-1[/math].

Таким образом, в параллельном варианте, в отличие от последовательного, вычисления делений будут определять довольно значительную долю требуемого времени. При реализации на конкретных архитектурах наличие в отдельных ярусах ЯПФ отдельных делений может породить и другие проблемы. Например, при реализации метода обратной подстановки на ПЛИСах остальные вычисления (умножения и сложения/вычитания) могут быть конвейеризованы, что даёт экономию и по ресурсам на программируемых платах; деления из-за их изолированности приведут к занятию ресурсов на платах, которые будут простаивать большую часть времени.

При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности, а в параллельном варианте это означает, что практически все промежуточные вычисления для выполнения алгоритма в режиме накопления должны быть двойной точности. В отличие от последовательного варианта это означает некоторое увеличение требуемой памяти.

При классификации по высоте ЯПФ, таким образом, метод обратной подстановки относится к алгоритмам с линейной сложностью. При классификации по ширине ЯПФ его сложность также будет линейной.

1.9 Описание входных и выходных данных

Входные данные: верхняя треугольная матрица [math]U[/math] (элементы [math]u_{ij}[/math]), вектор правой части [math]y[/math] (элементы [math]y_{i}[/math]).

Объём входных данных: [math]\frac{n (n + 3)}{2}[/math] (в силу треугольности достаточно хранить только диагональ и наддиагональные элементы матрицы [math]U[/math]).

Выходные данные: вектор решения [math]x[/math] (элементы [math]x_{i}[/math]).

Объём выходных данных: [math]n[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейным (отношение квадратической к линейной).

При этом вычислительная мощность алгоритма обратной подстановки, как отношение числа операций к суммарному объему входных и выходных данных – всего лишь константа.

При этом алгоритм обратной подстановки полностью детерминирован. Использование другого порядка выполнения ассоциативных операций в данной версии нами не рассматривается, поскольку в корне меняет структуру алгоритма и делает параллельную сложность квадратической.

Наличие линейного количества ярусов ЯПФ, состоящих из одного-единственного деления, потенциально замедляющее параллельные реализации алгоритма, является его характерным "узким местом", особенно в сравнении со схожей по решаемой математической задаче прямой подстановке, где диагональные элементы единичны. В связи с этим для решения СЛАУ предпочтительны такие разложения, содержащие треугольные матрицы, где в треугольных матрицах диагональные элементы единичны. В тех же случаях, когда получаются неособенные треугольные матрицы, их желательно предварительно, до решения СЛАУ с ними, преобразовать в произведение диагональной и треугольной с единичными диагональными элементами.

2 Программная реализация

2.1 Особенности реализации последовательного алгоритма

В простейшем варианте метод обратной подстановки на Фортране можно записать так:

        X(N) = Y(N) / U (N, N)
	DO  I = N-1, 1, -1
		S = Y(I)
		DO  J = N, I+1, -1
			S = S - DPROD(U(I,J), X(J))
		END DO
		X(I) = S / U(I,I)		
	END DO

При этом для реализации режима накопления переменная [math]S[/math] должна быть двойной точности.

2.2 Описание локальности данных и вычислений

2.2.2 Описание локальности реализации алгоритма

2.2.2.1 Описание структуры обращений в память и качественная оценка локальности

Рисунок 12.1. Обратный ход метода Гаусса решения СЛАУ. Общий профиль обращений в память

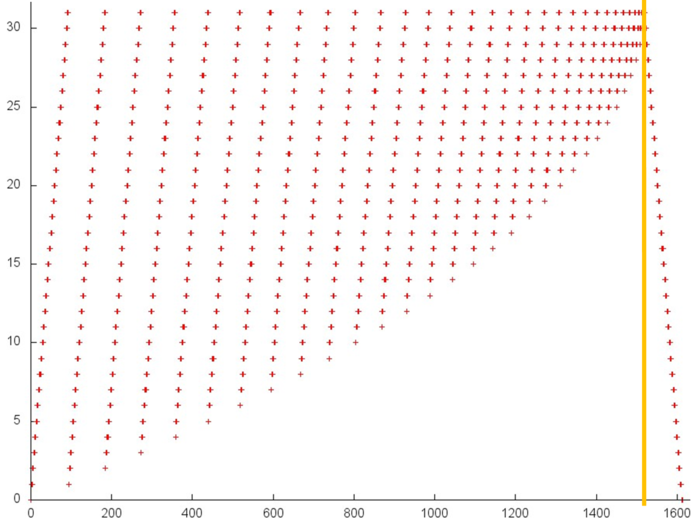
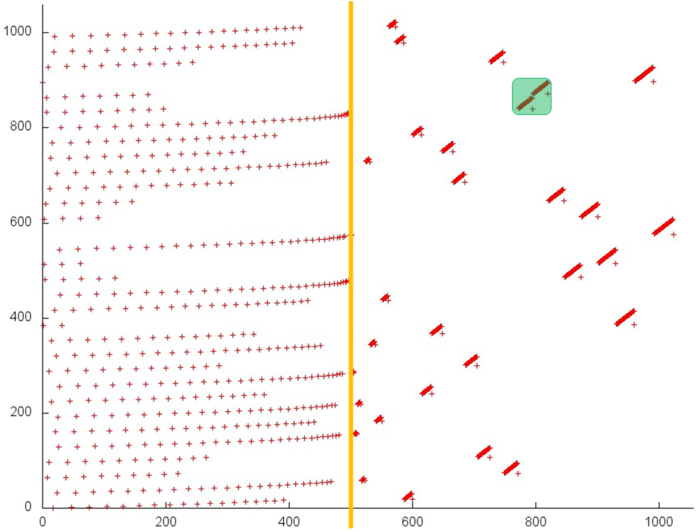
На рисунке 12.1 представлен профиль обращений в память для обратного хода метода Гаусса решения СЛАУ. Хорошо видно, что профиль состоит из двух этапов, идущих друг за другом (граница между ними выделена оранжевой линией). Это соответствует двум циклам, из которых собственно состоит исходный код обратного хода метода Гаусса. Из самого рисунка это заметить достаточно сложно, но анализ исходного кода показывает, что профиль образуется из обращений к 4 массивам. Три из них выделены на рис. 12.1 зеленым; к четвертому относятся все остальные обращения. Сразу отметим, что в данном профиле общее число обращений всего в несколько раз больше числа задействованных элементов массивов (4500 против 1000), а в таких условиях сложно добиться высокой локальности.

Чтобы выяснить это, перейдем к подробному рассмотрению каждого из массивов в отдельности.

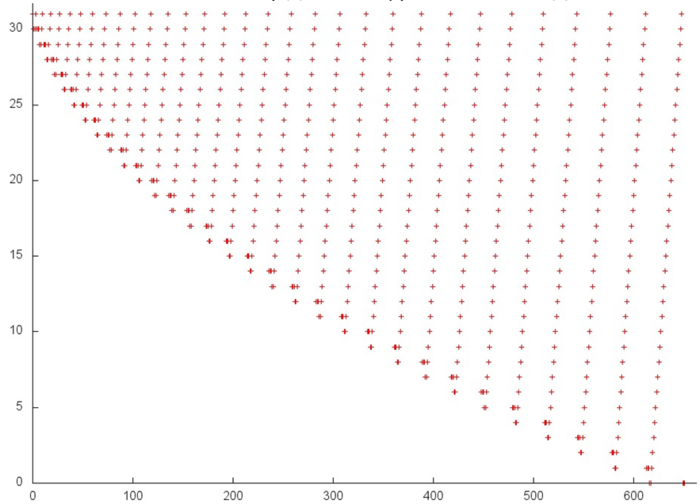
На рис. 12.2 представлен фрагмент 1. Оранжевой линей также проведено разделение 2 этапов. Видно, что второй этап устроен очень просто и представляет собой последовательный перебор в обратном порядке. Первый этап имеет итерационный характер, причем на каждой итерации отбрасывается элемент массива с наименьшим номером. Подобный профиль характеризуется высокой пространственной локальностью, поскольку элементы перебираются подряд; достаточно высокой временной локальностью, поскольку на каждой итерации происходит повторное обращение к тем же элементам.

Рисунок 12.2. Фрагмент 1 (профиль обращений к первому массиву)

На рис. 12.3 представлен фрагмент 2, показывающий обращения ко второму массиву. Сразу заметим, что данный фрагмент еще меньше предыдущего – здесь задействовано всего 600 обращений в память. По сути, данный фрагмент является аналогичным этапу 1 фрагмент 1, с единственной разницей – здесь итерации расположены в обратном порядке. Однако это изменение не оказывает особого влияния ни на пространственную, ни не временную локальность, поэтому данный фрагмент обладает теми же свойствами.

Рисунок 12.3. Фрагмент 2 (профиль обращений ко второму массиву)

Далее рассмотрим фрагмент 3 (рис. 12.4). Здесь также оранжевой линией проведено разделение между двумя этапами, и также на второй этап приходится совсем немного обращений. Обращения на первом этапе образуют аналог случайного доступа, достаточно часто встречающийся, например, в случае косвенной адресации. При этом в некоторый момент к определенному элементу происходит достаточно много обращений подряд, после чего этот элемент более не используется. Такой профиль обычно характеризуется низкой пространственной и временной локальностью, что, однако, в данном случае в достаточной степени нивелируется малым числом задействованных элементов.

Рисунок 12.4. Фрагмент 3 (профиль обращений к третьему массиву)

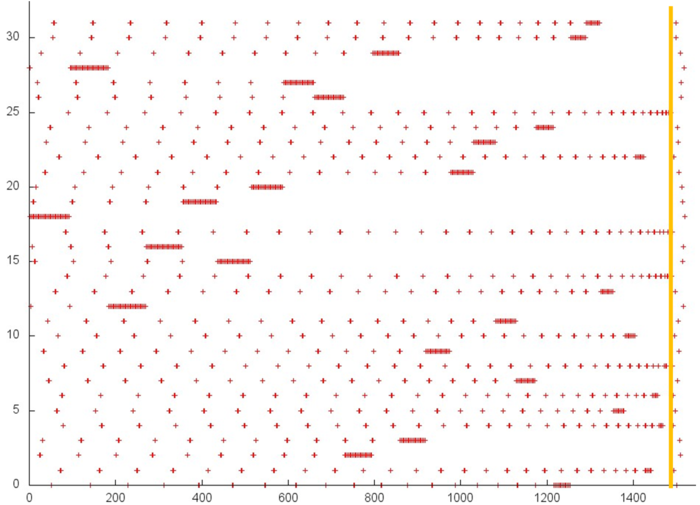
Далее перейдем к фрагменту, занимающему основную часть рис. 12.1. Данный профиль отображен на рис. 12.5. В первую очередь стоит отметить особенность данного профиля – здесь задействовано более 1000 элементов, в то время как в остальных профилям – порядка 30. При этом число обращений даже меньше, чем обращений к первому или третьему массиву.

Отметим также, что здесь большая часть обращений сосредоточена на втором этапе. Первый же этап является подобием первого этапа предыдущего массива (рис. 12.4) , за тем лишь исключением, что в данном профиле отсутствуют множественные обращения подряд к одному элементу перед тем, как элемент перестанет использоваться. С учетом того, что первый этап состоит всего из порядка 500 обращений, достаточно равномерно распределенных на отрезке в 1000 элементов, это говорит об очень низкой как пространственной, так и временной локальности.

Другой характер обращений можно наблюдать на втором этапе. Видно, что он обладает более высокой пространственной локальностью, так как обращения явно сгруппированы в кластеры, при этом кластеры обладают подобным строением. Однако структура самого кластера видно плохо, поэтому требуется дальнейшее приближение.

Рисунок 12.5. Фрагмент 4 (профиль обращений к четвертому массиву)

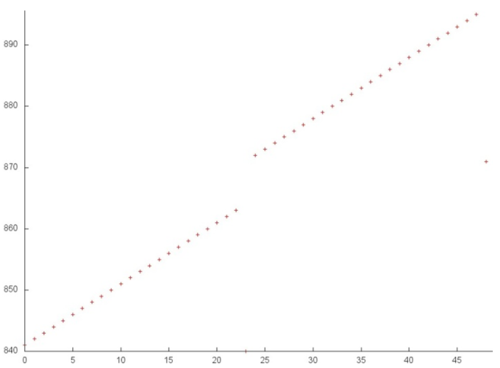
На рис. 12.6 показаны два кластера, выделенные на рис. 12.5 зеленым цветом. Такой масштаб позволяет сразу увидеть, что каждый кластер представляет собой последовательный перебор с небольшим шагом определенного набора элементов массива.

Следовательно, можно говорить о том, что второй этап фрагмента 4 обладает достаточно высокой пространственной локальностью (поскольку каждый кластер содержит последовательный перебор), но низкой временной локальностью (повторные обращения практически отсутствуют).

Рисунок 12.6. Два кластера из фрагмента 4

В целом по всему профилю можно сделать следующий вывод: первый три рассмотренных массива (особенно №1 и №2) обладают достаточно высокой локальностью, однако достаточно низкая пространственная и очень низкая временная локальность последнего массива в значительной степени снижают общую локальность всей программы.

2.2.2.2 Количественная оценка локальности

Основной фрагмент реализации, на основе которого были получены количественные оценки, приведен здесь (функция Kernel2). Условия запуска описаны здесь.

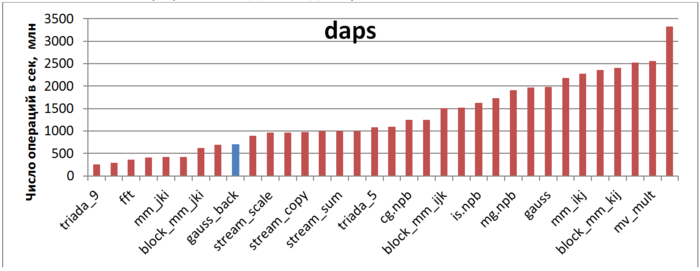
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.

На рисунке 12.7 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что, в соответствии с высказанным в предыдущем разделе предположением о негативном влиянии одного из массивов, данная программа показывает достаточно низкую производительность, заметно ниже, чем у прямого хода метода Гаусса.

Рисунок 12.7. Сравнение значений оценки daps

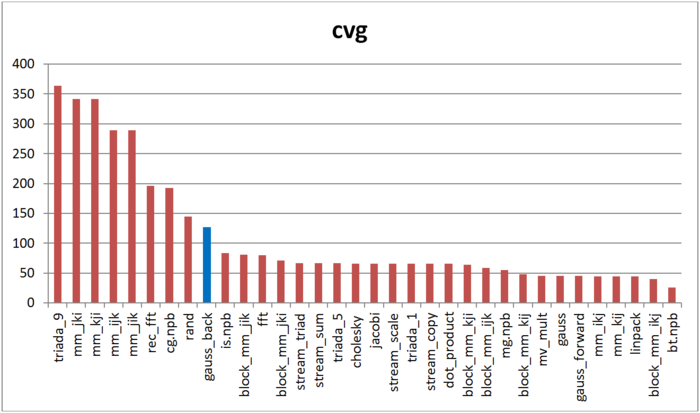
Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.

На рисунке 12.8 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, профиль обращений обладает низкой локальностью, лишь немногим лучше профиля программы со случайным доступом в память. Это повторяет выводы, сделанные на основе оценки daps.

Рисунок 12.8. Сравнение значений оценки cvg

3 Литература

1. В.В.Воеводин, Ю.А.Кузнецов. Матрицы и вычисления. - М.: Наука, 1984.
2. Дж.Форсайт, К.Моллер. Численное решение систем линейных алгебраических уравнений. - М.:Мир, 1969.