Участник:Бротиковская Данута/Алгоритм k-means

Алгоритм k средних (k means)
Последовательный алгоритм
Последовательная сложность	$O(\Tau*k*n*d)$
Объём входных данных	$n*d$
Объём выходных данных	$n$

Авторы страницы Данута Бротиковская и Денис Зобнин

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм k средних (k means) – неиерархический, итерационный метод кластеризации, получивший большую популярность благодаря своей простоте, наглядности реализации и достаточно высокому качеству работы. Был изобретен в 1950-х годах математиком Гуго Штейнгаузом и почти одновременно Стюартом Ллойдом. Особую популярность приобрел после публикации работы МакКуина в 1967.

Алгоритм представляет собой версию EM-алгоритма, применяемого также для разделения смеси гауссиан. Основная идея k-means заключается в том, что данные произвольно разбиваются на кластеры, после чего итеративно перевычисляется центр масс для каждого кластера, полученного на предыдущем шаге, затем векторы разбиваются на кластеры вновь в соответствии с тем, какой из новых центров оказался ближе по выбранной метрике.

Цель алгоритма заключается в разделении $n$ наблюдений на $k$ кластеров таким образом, чтобы каждое наблюдение придележало ровно одному кластеру, расположенному на наименьшем расстоянии от наблюдения.

1.2 Математическое описание алгоритма

Дано:

• набор из $n$ наблюдений $X=\{\mathbf{x}_1, \mathbf{x}_2, ..., \mathbf{x}_n\}, x_i \in \mathbb{R}^d, i=\overline{1, n}$;
• $k$ - требуемое число кластеров, $k \in \mathbb{N}, k\lt =n$;

Требуется:

Разделить множество наблюдений $X$ на $k$ кластеров $S_1, S_2, ..., S_k, S_i$:

• $\cap S_j= \varnothing, i \ne j$

• $\bigcup_{i=1}^{k} S_i = X$

Действие алгоритма:

Алгоритм k means разбивает набор $X$ на $k$ наборов $S_1, S_2, ..., S_k,$ таким образом, чтобы минимизировать сумму квадратов расстояний от каждой точки кластера до его центра (центр масс кластера). Введем обозначение, $S=\{S_1, S_2, ..., S_k\}$. Тогда действие алгоритма k-means равносильно поиску:

$\arg\min_{S} \sum\limits_{i=1}^k \sum\limits_{x \in S_i} \rho(\mathbf{x}, \mathbf{\mu}_i )^2,$

$(1)$

где $\mathbf{\mu}_i$ – центры кластеров, $i=\overline{1,k}, \rho(v_1, v_2)$ - функция расстояния между $x$ и $\mu_i$

Шаги алгоритма:

1. Начальный шаг: инициализация кластеров

   Выбирается произвольное множество точек $\mu_i, i=\overline{1,k}$, рассматриваемых как начальные центры кластеров: $\mu_i^{(0)} = \mu_i, i=\overline{1, k}$

2. Распределение векторов по кластерам

   Шаг t: $\forall \mathbf{x}_i \in X, i=\overline{1,n}: \mathbf{x}_i \in S_j \iff j=\arg\min_{k}\rho(\mathbf{x}_i,\mathbf{\mu}_k^{(t-1)})^2$

3. Пересчет центров кластеров

   Шаг t: $\forall i=\overline{1,k}: \mu_i^{(t)} = \cfrac{1}{|S_i|}\sum_{x\in S_i}x$

4. Проверка условия останова:

      if [math]\exist i\in \overline{1,k}: \mu_i^{(t)} \ne \mu_i^{(t-1)}[/math] then
          t = t + 1;
          goto 2;
      else
          stop
   

1.3 Вычислительное ядро алгоритма

Вычислительным ядром являются шаги 2 и 3 приведенного выше алгоритма: распределение векторов по кластерам и пересчет центров кластеров.

Распределение векторов по кластерам предполагает вычисление расстояний между каждым вектором $\mathbf{x}_i \in X, i= \overline{1,n}$ и центрами кластера $\mathbf{\mu}_j, j= \overline{1,k}$. Таким образом, данный шаг предполагает $k*n$ вычислений расстояний между d-мерными векторами.

Пересчет центров кластеров предполагает $k$ вычислений центров масс $\mathbf{\mu}_i$ множеств $S_i, i=\overline{1,k}$ представленных выражением в шаге 3 представленного выше алгоритма.

1.4 Макроструктура алгоритма

Инициализация центров масс $\mu_1, ..., \mu_k$.

Наиболее распространенными являются следующие стратегии:

• Метод Forgy
  В качестве начальных значений $\mu_1, ..., \mu_k$ берутся случайно выбранные векторы.
• Метод случайно разделения (Random Partitioning)
  Для каждого вектора $x_i \in X, i=\overline{1, n}$ выбирается случайным образом кластер $S_1, ..., S_k$, после чего для каждого полученного кластера вычисляются значения $\mu_1, ..., \mu_k$.

Распределение векторов по кластерам

Для этого шага алгоритма между векторами $x_i \in X, i=\overline{1, n}$ и центрами кластеров $\mu_1, ..., \mu_k$ вычисляются расстояния по формуле (как правило, используется Евлидово расстояние):

$v_1, v_2 \in \mathbb{R}^d, \rho(\mathbf{v_1}, \mathbf{v_2}) = \lVert \mathbf{v_1}- \mathbf{v_2} \rVert= \sqrt{\sum_{i=1}^{d}(v_1^i - v_2^i)}$

$(2)$

Пересчет центров кластеров

Для этого шага алгоритма производится пересчет центров кластера по формуле вычисления центра масс:

$\mu = \cfrac{1}{|S|}\sum_{x\in S}x$

$(3)$

1.5 Схема реализации последовательного алгоритма

algorithm k-means is
    1. Инициализировать центры кластеров [math]\mathbf{\mu}_i^{(1)}, i=\overline{1,k}[/math]
    2. [math]t \leftarrow 1[/math]
    3. Распределение по кластерам

       [math]S_i^{(t)}=\{\mathbf{x}_p: \lVert\mathbf{x}_p-\mathbf{\mu}_i^{(t-1)}\rVert^2 \leq \lVert\mathbf{x}_p-\mathbf{\mu}_j^{(t-1)}\rVert^2 \quad \forall j=\overline{1,k}\},[/math]

       где каждый вектор [math]\mathbf{x}_p[/math] соотносится единственному кластеру [math]S^{(t)}[/math]
    4. Обновление центров кластеров

       [math]\mathbf{\mu}_i^{(t)} = \frac{1}{|S^{(t)}_i|} \sum_{\mathbf{x}_j \in S^{(t)}_i} \mathbf{x}_j [/math]

    5. if [math]\exist i \in \overline{1,k}: \mathbf{\mu}_i^{(t)} \ne \mathbf{\mu}_i^{(t+1)}[/math] then
           t = t + 1;
           goto 3;
       else
           stop

1.6 Последовательная сложность алгоритма

Обозначим $\Theta_{centroid}^{d, m}$ временную сложность вычисления центорида кластера, число элементов которого равна $m$, в d-мерном пространстве.

Аналогично $\Theta_{distance}^d$ – временная сложность вычисления расстояния между двумя d-мерными векторами.

Сложность шага инициализации $k$ кластеров мощности $m$ в d-мерном пространстве – $\Theta_{init}^{k, d, m}$

• Стратерия Forgy: вычисления не требуются, $\Theta_{init}^{k, d, m} = 0$
• Стратегия случайного разбиения: вычисление центров $k$ кластеров, $\Theta_{init}^{k, d, m} = k*\Theta_{centroid}^{d, m}, m \le n$

Cложность шага распределения d мерных векторов по $k$ кластерам – $\Theta_{distribute}^{k, d}$

На этом шаге для каждого вектора $x_i \in X, i=\overline{1, n}$ вычисляется k расстояний до центров кластеров $\mu_1, ...\mu_k$

$\Theta_{distribute}^{k, d} = n*k*\Theta_{distance}^d$

Сложность шага пересчета центров $k$ кластеров размера $m$ в d-мерном пространстве – $\Theta_{recenter}^{k, d, m}$

На этом шаге вычисляется $k$ центров кластеров $\mu_1, ...\mu_k$

$\Theta_{recenter}^{k, d, m} = k*\Theta_{centroid}^{d, m}$

Рассчитаем $\Theta_{centroid}^{d, m}$ для кластера, число элементов которого равно $m$

$\Theta_{centroid}^{d, m}$ = $m * d$ сложений + $d$ делений

Рассчитаем $\Theta_{distance}^d$ в соответствие с формулой $(2)$

$\Theta_{distance}^d$ = $d$ вычитаний + $d$ умножений + $(d-1)$ сложение

Предположим, что алгоритм сошелся за $\Tau$ итераций, тогда временная сложность алгоритма $\Theta_{k-means}^{d, n}$

$\Theta_{k-means}^{d, n} \le \Theta_{init}^{k, d, n} + \Tau*(\Theta_{distribute}^{k, d} + \Theta_{recenter}^{k, d, n})$

Операции сложения/вычитания:

$\Theta_{k-means}^{d, n} \le k*n*d+ \Tau*(k*n*(2d-1) + k*n*d) = k*n*d+ \Tau*(k*n*(3d-1)) \thicksim O(\Tau*k*d*n)$

Операции умножения/деления:

$\Theta_{k-means}^{d, n} \le k*d + \Tau*(k*n*d + k*d) = k*d + \Tau * k*d*(n+1) \thicksim O(\Tau*k*d*n)$

Получаем, что временная сложность алгоритма k-means кластеризации $n$ d-мерных векторов на $k$ кластеров за $\Tau$ итераций:

$\Theta_{k-means}^{d, n} \thicksim O(\Tau*k*d*n)$

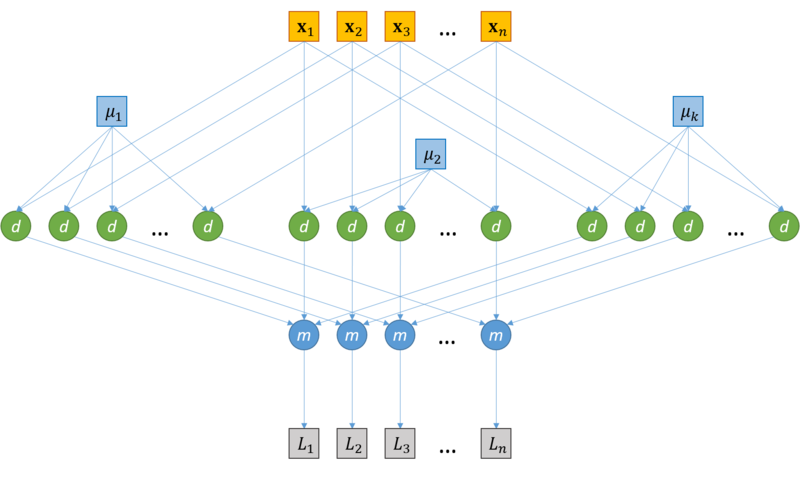
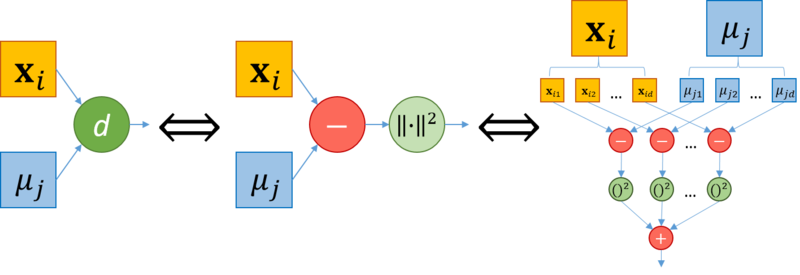
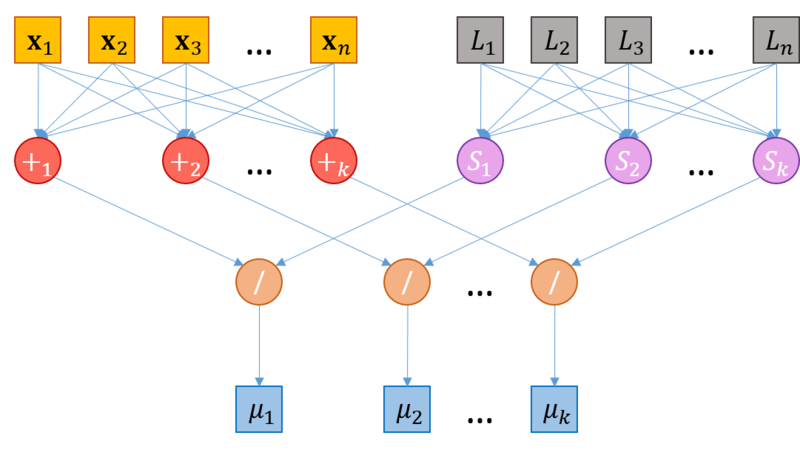
1.7 Информационный граф

Рис. 1. Схема распределения векторов по кластерам

Рис. 2. Схема вычисления расстояния между вектором и центром кластера.

Рис. 3. Схема пересчета центров кластеров

1.8 Ресурс параллелизма алгоритма

Работа алгоритма состоит из $\Tau$ итераций, в каждой из которых происходит распределение d-мерных векторов по $k$ кластерам+ пересчет центров кластеров в d-мерном пространстве. Вычислим параллельную сложность $\Psi_*$ каждого из шагов, а также параллельную сложность всего алгоритма, $\Psi_{k-means}$. Будем исходить из предположения, что может быть использовано любое необходимое число потоков.

Распределение d-мерных векторов по $k$ кластерам

Поскольку на данном шаге для каждой пары векторов $x_i, i=\overline{1,n}$ и $\mu_j, j=\overline{1,k}$ операции вычисления расстояния не зависят друг от друга, они могут выполняться параллельно. Тогда, разделив все вычисление расстояний на n потоков, получим, что в каждом потоке будет выполняться только одна операция вычисления расстояния между векторами размерности d. При этом каждому вычислительному потоку передаются координаты центров всех кластеров $\mu_1, ..., \mu_k$. Таким образом, параллельная сложность данного шага определяется сложностью параллельной операции вычисления расстояния между d-мерными векторами, $\Psi_{distance}^d$ и сложностью определения наиболее близкого кластера (паралельное взятие минимума по расстояниям), $\Psi_{min}^k$. Для оценки $\Psi_{distance}^d$ воспользуемся параллельной реализацией нахождения частичной суммы элементов массива путем сдваивания. Аналогично, $\Psi_{min}^k = log(k)$. В результате, $\Psi_{distance}^d = O(log(d))$. Таким образом:

$\Psi_{distribute}^{k, d} = \Psi_{distance}^d + \Psi_{min}^k = O(log(d))+O(log(k)) = O(log(k*d))$

Пересчет центров кластеров в d-мерном пространстве

Поскольку на данном шаге для каждого из $k$ кластеров центр масс может быть вычислен независимо, данные операции могут быть выполнены в отдельных потоках. Таким образом, параллельная сложность данного шага, $\Psi_{recenter}^{k, d}$, будет определяться параллельной сложностью вычисления одного центра масс кластера размера $m$,$\Psi_{recenter}^{k, d}$, а так как $m \le n \Rightarrow \Psi_{recenter}^{d, m} \le \Psi_{recenter}^{d, n}$. Сложность вычисления центра масс кластера d-мерных векторов размера n аналогично предыдущим вычислениям равна $O(log(n))$. Тогда:

$\Psi_{recenter}^{k, d} \le \Psi_{recenter}^{d, n} = O(log(n))$

Общая параллельная сложность алгоритма

На каждой итерации необходимо обновление центров кластеров, которые будут использованы на следующей итерации. Таким образом, итерационный процесс выполняется последовательно. Тогда, поскольку сложность каждой итерации определяется $\Psi_{distribute}^{k, d}$ и $\Psi_{recenter}$, сложность всего алгоритма, $\Psi_{k-means}$ в предположении, что было сделано $\Tau$ операций определяется выражением

$\Psi_{k-means} \approx \Tau * (\Psi_{distribute}^{k, d} + \Psi_{recenter}^{k, d}) \le \Tau * O(log(k*d*n))$

1.9 Входные и выходные данные алгоритма

Входные данные

• Целое положительное число $k$ – количество кластеров.
• Матрица из $n*d$ элементов – координат векторов (наблюдений).

Объем входных данных
$1$ целое число + $n*d$ вещественных чисел (при условии, что координаты – вещественные числа).

Выходные данные
Целые положительные числа – номера кластеров, соотвествующие каждому вектору (при условии, что нумерация кластеров начинается с 1).

Объем выходных данных
$n$ целых положительных чисел.

1.10 Свойства алгоритма

Вычислительная мощность

Вычислительная мощность алгоритма k means равна $\frac{k*d*n*\Tau}{n*d} = k*\Tau$, где $k$ – число кластеров, $\Tau$ – число итераций алгоритма.

Детерминированность и Устойчивость

Алгоритм k means является итерационным. Количество итераций алгоритма в общем случае не фиксируется и зависит от начального расположения объектов в пространстве, параметра $k$, а также от начального приближения центров кластеров, $\mu_1, ..., \mu_k$. В результате этого может варьироваться результат работы алгоритма. По этим причинам алгоритм не является ни детермирированным, ни устойчивым.

Сильные стороны алгоритма:

• Сравнительно высокая эффективность при простоте реализации
• Высокое качество кластеризации
• Возможность распараллеливания
• Существование множества модификаций

Недостатки алгоритма:

• Количество кластеров является параметром алгоритма

• Чувствительность к начальным условиям

  Инициализация центров кластеров в значительной степени влияет на результат кластеризации.

• Чувствительность к выбросам и шумам

  Выбросы, далекие от центров настоящих кластеров, все равно учитываются при вычислении их центров.

• Возможность сходимости к локальному оптимуму

  Итеративный подход не дает гарантии сходимости к оптимальному решению.

• Использование понятия "среднего"

  Алгоритм неприменим к данным, для которых не определено понятие "среднего", например, категориальным данным.

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

2.7.1 Открытое программное обеспечение

1. CrimeStat
Программное обеспечение, созданное для операционных систем Windows, предоставляющее инструменты статистического и пространственного анализа для решения задачи картирования преступности.
2. Julia
Высокоуровневый высокопроизводительный свободный язык программирования с динамической типизацией, созданный для математических вычислений, содержит реализацию k-means.
3. Mahout
Apache Mahout - Java библиотека для работы с алгоритмами машинного обучения с использованием MapReduce. Содержит реализацию k-means.
4. Octave
Написанная на C++ свободная система для математических вычислений, использующая совместимый с MATLAB язык высокого уровня, содержит реализацию k-means.
5. Spark
Распределенная реализация k-means содержится в библиотеке Mlib для работы с алгоритмами машинного обучения, взаимодействующая с Python библиотекой NumPy и библиотека R.
6. Torch
MATLAB-подобная библиотека для языка программирования Lua с открытым исходным кодом, предоставляет большое количество алгоритмов для глубинного обучения и научных расчётов. Ядро написано на Си, прикладная часть выполняется на LuaJIT, поддерживается распараллеливание вычислений средствами CUDA и OpenMP. Существуют реализации k-means.
7. Weka
Cвободное программное обеспечение для анализа данных, написанное на Java. Содержит k-means и x-means.
8. Accord.NET
C# реализация алгоритмов k-means, k-means++, k-modes.
9. OpenCV
Написанная на С++ библиотека, направленная в основном на решение задач компьютерного зрения. Содержит реализацию k-means.
10. MLPACK
Масштабируемая С++ библиотека для работы с алгоритмами машинного обучения, содержит реализацию k-means.
11. SciPy
Библиотека Python, содержит множество реализаций k-means.
12. scikit-learn
Библиотека Python, содержит множество реализаций k-means.
13. R
Язык программирования для статистической обработки данных и работы с графикой, а также свободная программная среда вычислений с открытым исходным кодом в рамках проекта GNU, содержит три реализации k-means.
14. ELKI
Java фреймворк, содержащий реализацию k-means, а также множество других алгоритмов кластеризации.

2.7.2 Проприетарное программное обеспечение

1. Ayasdi
2. Stata
3. Mathematica
4. MATLAB
5. SAS
6. RapidMiner
7. SAP HANA