Участник:Евгений Раев/Построение матрицы Адамара произвольного размера
| Построение матрицы Адамара произвольного размера | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(n^2)[/math] |
| Объём входных данных | [math]1[/math] |
| Объём выходных данных | [math]n^2[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]?[/math] |
| Ширина ярусно-параллельной формы | [math]O(n^2)[/math] |
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Матрица Адамара [math]H[/math] — это квадратная матрица размера n×n, составленная из чисел 1 и −1, столбцы которой ортогональны, так что справедливо соотношение
- [math]H \cdot H^T = n \cdot E_n,[/math]
где [math]E_n[/math] — это единичная матрица размера n. Матрицы Адамара применяются в различных областях, включая комбинаторику, численный анализ, обработку сигналов.
Матрица оператора Адамара имееет вид
- [math]\begin{align} H = \frac{1}{\sqrt2} &\begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix} \end{align}[/math]
Соответственно, существует итерационная формула нахождения матриц Адамара, через тензорное произведение матрицы оператора Адамара на матрицу Адамара меньшего порядка:
- [math]H_n = H_{1} \otimes H_{n-1}[/math]
Мы будем использовать в дальнейшем нормализованную матрицу оператора Адамара, без коэффицента (для удобности вывода):
- [math]\begin{align} H = &\begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix} \end{align}[/math]
Представим пример высчитывания матриц Адамара:
- [math] H_{0} = 1, [/math]
- [math] H_{1} = H_{1} \otimes H_{0} = \begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix} \otimes 1 = \begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix}, [/math]
- [math] H_{2} = H_{1} \otimes H_{1} = \begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix} \otimes \begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix} = \begin{pmatrix}\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1 \end{array}\end{pmatrix} [/math]
- [math] H_{3} = H_{1} \otimes H_{2} = \begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix} \otimes \begin{pmatrix}\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1 \end{array}\end{pmatrix} = \begin{pmatrix}\begin{array}{rrrrrrrr} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1 & 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1 & 1 & -1 & -1 & 1\\ 1 & 1 & 1 & -1 & -1 & -1 & -1 & -1\\ 1 & -1 & 1 & 1 & -1 & 1 & -1 & 1\\ 1 & 1 & -1 & 1 & -1 & -1 & 1 & 1\\ 1 & -1 & -1 & -1 & -1 & 1 & 1 & -1\\ \end{array}\end{pmatrix} [/math]
Таким образом, получаем последовательность матриц Адамамра размерностью [math]2^n[/math]
[math]H^{\otimes n} = H_1 \otimes ... \otimes H_1[/math], где знак [math] \otimes [/math] означает тензорное произведение.
1.2 Математическое описание алгоритма
Тензорное произведение довольно затратно для реализации на вычислительной технике (необходимо хранить в памяти матрицу предыдущего порядка), поэтому существует формула для определения элемента матрицы Адамара по его индексам:
- [math]H_{i,j} = (-1)^{\sum i_{2 } j_{2 }}[/math], где [math]i_{2}[/math] и [math]j_{2}[/math] - битовые представляения значений индексов, а [math]i_{2 } j_{2 }[/math] - побитовое умножение.
То есть, знак элемента матрицы Адамара зависит от количества едининц в побитовом произведении индексов - если это число чётное - то знак положительный, если нечётное - отрицательный.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро расчете элементов матрицы Адамара это вычисление элемента матрицы Адамара по его индексам:
- [math]H_{i,j} = (-1)^{\sum i_{2 } j_{2 }}[/math]
Данная операция независима для каждого элемента, соответственно именно она подлежит распараллеливанию.
1.4 Макроструктура алгоритма
В вычислительном ядре используется операция опеределения четности суммы значачих единиц в результате побитового умножения двух чисел.
1.5 Схема реализации последовательного алгоритма
Последовательность исполнения метода следующая:
1. Определение индексов находимого элемента матрицы Адамара: [math]i[/math] и [math]j[/math].
2. Побитовое умножение индексов : [math]res = i_{2} j_{2}[/math].
3. Подсчет количества значащих единиц в [math]res[/math]: [math]count = \sum res[/math].
4. Получение знака элемента: [math]sign = (-1)^{count}[/math].
Данному алгоритму соответствует приведенный ниже код на языке С++:
#include <iostream>
#include <cmath>
#include <stdio.h>
#include <stdlib.h>
using namespace std;
int get_sign(int i, int j) //Get sign Hadamard matrix's element by indices
{
int res = i & j;
int count;
for (count=0; res; res>>=1)
{
if (res & 1)
count++;
}
if (count & 1 ==1)
return -1;
else
return 1;
}
int print_HadamardMatrix(int N) //print Hadamard matrix 2^n size
{
int matr_size(pow(2,N));
for (int i = 0; i < matr_size; i++)
{
for (int j = 0; j < matr_size; j++)
{
if (get_sign(i,j)==1)
cout <<" 1 ";
else
cout <<"-1 ";
}
cout << endl;
}
cout << endl;
return 0;
}
int main(int argc, const char * argv[])
{
if(argc!=2)
{
printf("Matrix size missing\n");
return 1;
}
int N(atoi(argv[1]));
print_HadamardMatrix(N);
return 0;
}
1.6 Последовательная сложность алгоритма
Построение матрицы Адамара порядка [math]N = 2^n[/math] требует:
1. [math]N^2[/math] побитовых умножений [math]ij[/math]
2. [math]N[/math] операций сдвига.
3. Првиет
Для построения матрицы Адамара порядка [math]N=2^n[/math] в первом шаге потребуется [math]N^2[/math] побитовых умножений k&l. Во втором шаге, как говорилось выше, сложность метода вычисления количества единиц числа в двоичном представлении равна удвоенному количеству единиц. В наихудшем случае сложность равна [math]2log_2N[/math], при k=l=N-1, а в наилучшем 0. Для нахождения степени всех элементов матрицы потребуются [math] 2N^2[\frac{log_2N}{4}][/math] операций. В третьем шаге для определения знака потребуется [math]N^2[/math] операций.
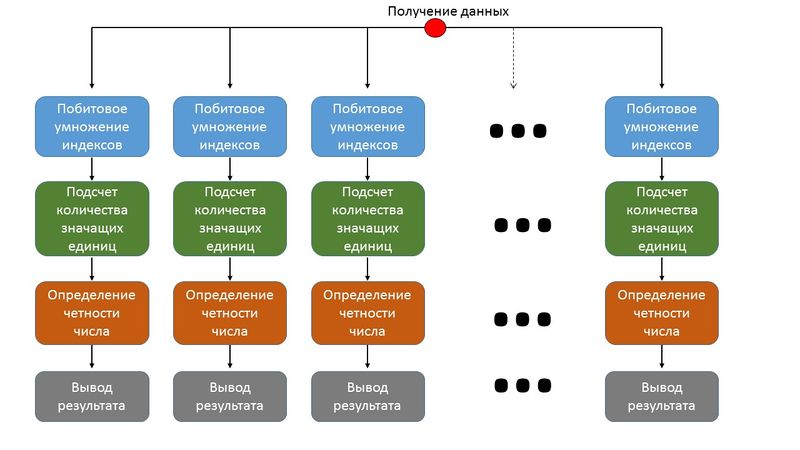
1.7 Информационный граф
На рисунке ниже изображен информационный граф алгоритма.
1. Побитовое умножение индексов.[math]i_{2}j_{2}[/math], где [math]i[/math] и [math]j[/math] соответствующие координаты элемента [math]h_{kl}[/math];
2. Подсчет количества значащих единиц. Состоит из последовательных сдвигов и побитового "И" с 1.
3. Определение четности количества - побитовое "И" количества значащих единиц с 1.
1.8 Ресурс параллелизма алгоритма
1.9 Входные и выходные данные алгоритма
Входные данные: n - размерность матрицы [math]H_n[/math].
Объём входных данных: 1 (число n).
Выходные данные: матрица Адамара [math]H_{n}[/math] размерностью [math]2^n[/math].
Объём выходных данных: [math]2^{n+n}[/math].
1.10 Свойства алгоритма
- Соотношение последовательной и параллельной сложности является линейным.
- Алогритм построения матрицы Адамара не является детерминированным.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.2.1 Локальность реализации алгоритма
2.2.1.1 Структура обращений в память и качественная оценка локальности
2.2.1.2 Количественная оценка локальности
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
2.4.2 Масштабируемость реализации алгоритма
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
3 Литература
[1] Кронберг, Ю.И. Ожигов, А.Ю. Чернявский — Алгебраический аппарат квантовой информатики 2
[2] Википедия – свободная энциклопедия [Электронный ресурс]. - https://en.wikipedia.org/wiki/Hadamard_transform. - (дата обращения: 15.10.2016).