Участник:Алексей Будюк/Метод Якоби вычисления собственных значений симметричной матрицы

Основные авторы описания: А.М. Будюк, В.А. Сальников

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Целый ряд инженерных задач сводится к рассмотрению систем уравнений, имеющих единственное решение лишь в том случае, если известно значение некоторого входящего в них параметра. Этот особый параметр называется характеристическим, или собственным значением системы. С задачами на собственные значения инженер сталкивается в различных ситуациях. Так, для тензоров напряжений собственные значения определяют главные нормальные напряжения, а собственными векторами задаются направления, связанные с этими значениями. При динамическом анализе механических систем собственные значения соответствуют собственным частотам колебаний, а собственные вектора характеризуют моды этих колебаний. При расчете конструкций собственные значения позволяют определять критические нагрузки, превышение которых приводит к потере устойчивости.
Таким образом, задача нахождения собственных значений и собственных векторов матриц (СЗВМ) является одной из основных задач для многих разделов физики. Одним из методов решения является метод Якоби. Этот метод позволяет привести матрицу к диагональному виду, последовательно, исключая все элементы, стоящие вне главной диагонали. В итоге, накопление в процессе преобразований произведения трансформационных матриц дает матрицу собственных векторов, в то время как диагональные элементы являются собственными значениями. К сожалению, приведение к строго диагональному виду, в общем случае, требует бесконечно большого числа шагов, так как образование нового нулевого элемента на месте одного из элементов матрицы часто ведет к появлению ненулевого элемента там, где ранее был нуль, так как при преобразовании затрагиваются и другие элементы матрицы. На практике метод Якоби рассматривают, как итерационную процедуру, которая в принципе позволяет с заданной точностью подойти к диагональной форме.
В случае симметричной матрицы [math]A[/math] действительных чисел преобразование выполняется с помощью ортогональных матриц [math]P[/math], полученных в результате вращении в действительной плоскости. Вычисления осуществляются следующим образом. Из исходной матрицы [math]A[/math] образуют матрицу [math]A_1[/math], при этом ортогональная матрица плоского вращения [math]P_1[/math] выбирается так, чтобы в матрице [math]A_1[/math] появился нулевой элемент, стоящий вне главной диагонали (обычно выбирается наибольший по модулю элемент). Затем из [math]A_1[/math] с помощью второй преобразующей матрицы [math]P_2,[/math] образуют новую матрицу [math]A_2[/math]. При этом [math]P_2[/math], выбирают так, чтобы в [math]A_2[/math] появился еще один нулевой внедиагональный элемент. Эту процедуру продолжают, стремясь, чтобы на каждом шаге в нуль обращался наибольший внедиагональный элемент. В итоге получаем некоторый бесконечный итерационный процесс, на каждом шаге которого преобразующаяся матрица становится всё более и более близкой к диагональной форме (в смысле уменьшения суммы квадратов всех своих недиагональных элементов). На практике, при решении задач, выбирается некоторая величина [math]\epsilon[/math], и итерационный процесс останавливается, когда наибольший по модулю внедиагональный элемент становится меньше [math]\epsilon[/math].

1.2 Математическое описание алгоритма

Пусть [math]A=(a_{ij})[/math] симметричная матрица, а [math]P(i,j,\theta)[/math] ортогональная матрица, называемая вращением Якоби, зависящая от параметра [math]\theta[/math], тогда итерационная последовательность строится следующим образом:

[math] A_k = P_k^TA_{k-1}P_k [/math]

Матрицы [math] A_i[/math] образуют итерационную последовательность симметричных матриц, сходящуюся к диагональной матрице из собственных значений [math]D[/math]. А так как

[math] A_k = P_k^TA_{k-1}P_k = P_k^TP_{k-1}^TA_{k-2}P_kP_{k-1} = ... = P^TA_1P [/math],

то матрицы вращений образуют матрицу из собственных векторов [math]P=P_kP_{k-1}..P_1[/math]. Матрица вращения [math]P(i,j,\theta)[/math] имеет следующий вид:

[math]P(i,j,\theta)=\begin{pmatrix} 1 & & & & & & 0 \\ &\ddots & & & & & \\ & & cos(\theta) & & sin(\theta) & & \\ & & & \ddots & & & \\ & & -sin(\theta) & & cos(\theta) & & \\ & & & & &\ddots & \\ 0 & & & & & & 1 \end{pmatrix} [/math]

Где синусы и косинусы стоят только на [math]i[/math] и [math]j[/math] позициях.
Если же мы произведём матричное умножение [math]P_k^TA_kP_k[/math], то в результате первого умножения [math]P_k^TA_k[/math] изменит только строки [math]i[/math] и [math]j[/math] матрицы [math]A_k[/math], в то время как [math]A_kP_k[/math] меняет только столбцы [math]i[/math] и [math]j[/math]. Таким образом изменённые элементы расположены только в строках и столбцах [math]i[/math] и [math]j[/math] матрицы [math]A_k[/math]. Поэтому логичнее вычислять именно эти элементы по следующим формулам (которые на самом деле и есть результат перемножения матриц), чем полностью перемножать матрицы:

[math] \begin{align} a_{ii}^{k+1}&=c^2a_{ii}^k-2sca_{ij}^k+s^2a_{jj}^k \\ a_{jj}^{k+1}&=s^2a_{ii}^k+2sca_{ij}^k+c^2a_{jj}^k \\ a_{ij}^{k+1}&=a_{ji}^{k+1}=(c^2-s^2)a_{ij}^k+sc(a_{ii}^k-a_{jj}^k)\\ a_{il}^{k+1}&=a_{li}^{k+1}=ca_{il}^k-sa_{jl}^k\\ a_{jl}^{k+1}&=a_{lj}^{k+1}=sa_{il}^k+ca_{jl}^k\\ a_{lm}^{k+1}&=a_{ml}^k,\\ \end{align} [/math]

[math] l,m\neq i,j [/math]

Приравнивая внедиагональный элемент к нулю, получаем формулы для параметра [math]\theta[/math]: [math]r=ctg(2\theta)=\frac{c^2-s^2}{2sc}=\frac{a_{jj}-a_{ii}}{2a_{ij}}[/math]

[math]tg(\theta)=t=\frac{sign(r)}{|r|+\sqrt{1+r^2}}[/math]

[math]c=\frac{1}{\sqrt{1+t^2}}[/math]

[math]s=ct[/math]

Если [math]a_{jj}=a_{ii}[/math] то [math]\theta=\frac{\pi}{4}[/math]

1.3 Вычислительное ядро алгоритма

Основные вычислительные затраты:

1. Достаточно затратная операция сравнения в количестве [math]\frac{n(n-1)}{2}-1[/math] для нахождения максимума внедиагональных элементов и получения его индексов.
2. Пересчёт элементов массива, изменённых при вращении, в [math]i[/math] и [math]j[/math] строках и столбцах в количестве [math]4(n-1)[/math] по формулам, описанным выше.

1.4 Макроструктура алгоритма

На макроуровне выделяем 4 основных операции:

1. Выбор обнуляемого элемента (поиск максимального внедиагонального элемента)
2. Проверка условия остановки алгоритма (сравнение с [math]\epsilon[/math])
3. Вычисление параметров вращения
4. Применение вращения (пересчёт элементов матрицы)

1.5 Схема реализации последовательного алгоритма

Выбираем желаемый уровень точности [math]\epsilon[/math].

1. В матрице [math]A_k, \;\; k=0,1,...[/math]   выбрать среди всех внедиагональных элементов(достаточно рассмотреть, например, только наддиагональные) максимальный по модулю [math]a^k_{i_kj_k},\;\; i_k\lt j_k[/math]   и запомнить его индексы.
2. Для выбранного [math]\epsilon[/math] проверяется условие: [math]|a^k_{i_kj_k}|\lt \epsilon[/math]. Если условие не выполнено, то перейти к п.3, иначе завершить процесс.
3. Для данного элемента матрицы вычислить параметры поворота [math]c=cos(\theta)[/math] и [math]s=sin(\theta)[/math] для матриц [math]P_k[/math].
4. Применить поворот: [math]A_{k+1}=P_k^TA_kP_k[/math], пересчитав элементы матрицы [math]A_k[/math] по формулам приведённым выше.
5. Перейти на п.1

1.6 Последовательная сложность алгоритма

1. Для поиска максимального элемента, как уже говорилось ранее, нам требуется [math]\frac{n(n-1)}{2}-1[/math] сравненинй.
2. Сравнение для условия остановки.
3. Для вычисления параметров поворота: 3 деления, 4 умножения, 4 сложения(вычитания), 2 операции взятия корня.
4. Для пересчёта элементов матрицы: [math]4n+6[/math] умножений и [math]2n[/math] сложений.

Итого, перебирая в общем случае все [math]\frac{n(n-1)}{2}[/math] внедиагональные элементы матрицы, без сравнения получаем сложность алгоритма [math]O(n^3)[/math], что в принципе соответствует сложности перемножения матриц.

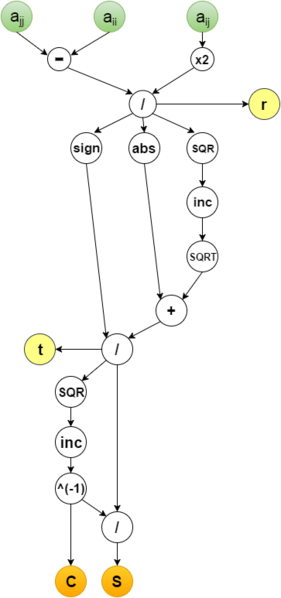
1.7 Информационный граф

Опишем алгоритм как аналитически, так и в виде рисунка.

Группе вершин A соответствует вычисление модуля максимума среди наддиагональных элементов.

Группе вершин B соответствует сравнение элемента [math]|a^k_{i_kj_k}|[/math] с заданным параметром [math]\epsilon[/math]. Если [math]|a^k_{i_kj_k}|\lt \epsilon[/math], то переходим к группе вершин C, иначе завершается работа алгоритма.

Группе вершин C соответствует вычисление параметров поворота [math]c=cos(\theta)[/math] и [math]s=sin(\theta)[/math] для матриц [math]P_k[/math].

Группе вершин D соответствует операция поворота матрицы [math]A_k[/math] по формулам пересчета элементов матрицы. Таких групп вершин на данном этапе [math]2*(n-1)[/math]

• 

  Рисунок 1. Граф одной итерации алгоритма с входными и выходными параметрами

• 

  Рисунок 2. Граф вершин C с входными и выходными параметрами

1.8 Ресурс параллелизма алгоритма

Наш алгоритм является итерационным и соответственно каждая итерация последовательна, что видно на информационном графе.

Рассмотрим одну итерацию:

1. На шаге вычисления параметров высота ярусно-парралельной формы(ЯПФ) равна 11, а ширина 3.
2. Основной ресурс парралелизма заложен на шаге пересчёта элементов матрицы. Ярус имеет ширину [math]2n-2[/math].    На [math]2n-4[/math] его узлах выпоняется последовательно 2 умножения и 1 сложение(вычитание) для элементов [math]a_{im}^{(k+1)} = a_{mi}^{(k+1)}[/math]   и   [math]a_{jm}^{(k+1)} = a_{mj}^{(k+1)}[/math],   [math]m \ne i,j[/math]   и на 2 узлах последовательно 7 умножений и 2 сложения(вычитания) для элементов [math]a_{ii}^{(k+1)} [/math]   и   [math]a_{jj}^{(k+1)} [/math]. Таким образом, имея неограниченное количетво процесоров, этот шаг выполняется за константное количество операций.

В итоге основная сложность парралельного алгоритма заключается в последовательном выполнении итераций в количестве [math]\frac{n(n-1)}{2}[/math]. В результате чего сложность получается [math]O(n^2)[/math], а по ширине ЯПФ [math]O(n)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: симметрическая матрица [math]A=(a_{ij})[/math].

Объём входных данных: матрица размера [math]n\times n[/math], но из-за симетричности достаточно хранить только диагональ и над/поддиагональные элементы и объём сокращается до   [math]\frac{n (n + 1)}{2}[/math].

Выходные данные: вектор собственных значений [math]\Lambda[/math] матрицы [math]A[/math].

Объём выходных данных: вектор размера [math] n [/math].

1.10 Свойства алгоритма

Как было видно ранее, парралельный алгоритм не дал сильного выигрыша в сложности. Соотношение последовательной и параллельной сложности равняется [math]O(n).[/math]
При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данны также имеет порядок [math]O(n).[/math]
Отметим, что для симметричной матрицы задача нахождение собственных значений симметричной матрицы является устойчивой.
Касательно вопроса сбалансированности вычислительного процесса можно отметить, что умножений в 2 раза больше сложений(вычитаний). Обращения в память зависят от конкретной реализации, использование кешей, и т.д. Имеет место сбалансированность операций между параллельными ветвями алгоритма.
Итерационный метод Якоби является недетерминированным: число итераций, а значит и число операций, меняется в зависимости от входных данных и параметра точности [math]\epsilon[/math].
Степень исхода из вершины С

3 Литература

[1] Ильин В.А., Позняк Э.Г. Линейная алгебра М.: 1974, «Наука», 292 c.

[2] Г.М. Чечиным М.Ю. Зехцером. "Собственные значения и собственные векторыматрицц" Часть 1: Теоретические аспекты 2006 г