Эта работа ждет рассмотрения преподавателем
Дата последней правки страницы: 15.10.2016
Авторы этой статьи считают, что задание выполнено.

Плотностный алгоритм кластеризации DBSCAN
Последовательный алгоритм
Последовательная сложность	[math]O(n \log n)[/math]
Объём входных данных	[math]n[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(\|H\| \log \|H\|)[/math]
Ширина ярусно-параллельной формы	[math]O(w)[/math]

Основной автор описания: Гилевич В.В.

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Кластеризация — это процедура, упорядочивающая элементы из некоторого множества в сравнительно однородные группы (кластеры). Элементы могут содержать числовые, категориальные или смешанные данные. Плотностные методы выделяют кластеры на основе следующей идеи: кластером считается регион с высокой плотностью объектов, которые разделены разреженными регионами (с низкой плотностью объектов)

Алгоритм DBSCAN (Density Based Spatial Clustering of Applications with Noise) ^[1] — плотностной алгоритм для кластеризации пространственных данных с присутствием шума, был предложен Мартином Эстер, Гансом-Питером Кригель и их коллегами в 1996 году как решение проблемы разбиения данных на кластеры произвольной формы.

1.2 Математическое описание алгоритма

1.2.1 Исходные данные

Множество [math]X[/math], на котором определена функция расстояния [math]D[/math].

1.2.2 Вычисляемые данные

Множество пар из элемента множества [math]X[/math], и соответствующий ему номер кластера.

1.2.3 Параметры алгоритма

[math]\varepsilon[/math] — максимальное расстояние между соседями;
[math]MinPts[/math] — минимальное количество элементов находящихся [math]\varepsilon[/math]-окрестности данного элемента для создания кластера.

1.2.4 Определения

ядровой элемент: элемент [math]p[/math] является ядровым, если количество элементов в [math]\varepsilon[/math]-окрестности, включая сам элемент [math]p[/math] больше или равно [math]MinPts[/math];

достижимость напрямую элемента [math]p[/math] из элемента q: элемент [math]p[/math] считается достижимым напрямую из элемента [math]q[/math], если элемент [math]q[/math] является ядровым, а элемент [math]p[/math] находится в [math]\varepsilon[/math]-окрестности элемента q;

достижимость элемента [math]p[/math] из элемента [math]q[/math]: элемент [math]p[/math] достижим из элемента [math]q[/math], если существует путь [math]p_1, \dots, p_n[/math], где [math]p_1 = p[/math] и [math]p_n = q[/math], где [math]p_{i + 1}[/math] напрямую достижим из [math]p_{i}[/math];

шум: все элементы, недостижимые из какого-либо другого считаются шумом.

Так как достижимость не является симметричным отношением (никакой элемент не может быть достижим из неядрового, вне зависимости от расстояния), то предлагается ввести следующее отношение:

связанность элемента p и элемента q: элемент [math]p[/math] считается связанным с [math]q[/math], если существует такой элемент [math]o[/math], что [math]p[/math] и [math]q[/math] достижимы из него.

Таким образом кластер должен удовлетворять двум условиям:

Все элементы внутри кластера взаимно связанны;
Если элемент связан с каким-либо элементом кластера, то он тоже является частью кластера.

Рис. 1^[2]. Для MinPts = 4. Красные элементы соответствуют ядровым, желтые — достижимым, синяя — шуму.

1.2.5 Пошаговое описание алгоритма

Выбирается произвольная непосещенный элемент [math]p[/math].
Элемент [math]p[/math] помечается как посещенный.
Проверяется, является ли элемент [math]p[/math] ядровым.
- Если элемент [math]p[/math] является ядровым, то:
  - Он становится началом нового кластера или сохраняет номер кластера, который был присвоен элементу ранее;
  - Все элементы из [math]\varepsilon[/math]-окрестности элемента [math]p[/math] добавляются в его кластер (им присваевается номер кластера элемента [math]p[/math]);
  - Процесс продолжается рекурсивно для каждого непосещенного элемента текущего кластера c шага 2.
- Если элемент [math]p[/math] не является ядровым, то [math]p[/math] объявляется шумом. Алгоритм продолжается с шага 4.
Если остались непосещенные точки, то алгоритм продолжается с шага 1.

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма является поиск элементов в [math]\varepsilon[/math]-окрестности каждого элемента входного множества [math]X[/math]. На эту часть алгоритма приходится основное время работы алгоритма, так как для каждого элемента необходимо выполнить эту операцию.

1.4 Макроструктура алгоритма

Алгоритм DBSCAN предполагает использование пространственной структуры данных: такие структуры позволяют найти все элементы в пределах определенного расстояния от текущего за [math]O(\log n)[/math]. Сложность построения таких структур [math]O(n \log n)[/math], таким образом, использование такой структуры не увеличивает сложность всего алгоритма.

1.5 Схема реализации последовательного алгоритма

[math]DBSCAN(X, \varepsilon, MinPts)[/math]
  [math]C = 0[/math]
  for [math]p[/math] in [math]X[/math]:
    if [math]p[/math] is [math]visited[/math]:
      continue
    mark [math]p[/math] as [math]visited[/math]
    [math]neighbours[/math] = [math]\{ o \ | \ \forall o \in X: D(p, o) \le \varepsilon \}[/math]
    if [math]| neighbours | \ge MinPts[/math]:
      [math]C = C + 1[/math]
      add [math]p[/math] to cluster [math]C[/math]
      for [math]q \in neighbours[/math]:
        if [math]q[/math] is not [math]visited[/math]:
          mark [math]q[/math] as [math]visited[/math]
          [math]q\_neighbours[/math] = [math]\{ o \ | \ \forall o \in X: D(q, o) \le \varepsilon \}[/math]
          if [math]| q\_neighbours | \ge MinPts[/math]:
            [math]neighbours[/math] = [math]neighbours \cup q\_neighbours[/math]  
        if [math]q[/math] has no cluster mark:
          mark [math]q[/math] as part of cluster [math]C[/math]
    else:
      mark [math]p[/math] as [math]noise[/math]

1.6 Последовательная сложность алгоритма

Для того, чтобы проверить принадлежность элемента множества к кластеру необходимо получить список соседей в его [math]\varepsilon[/math]-окрестности. При использовании пространственной структуры данных данная операция может быть выполнена со сложностью [math]O(\log n)[/math]. Так как для необходимо определить принадлежность к кластеру всех элементов множества, то сложность самого алгоритма [math]O(n \log n)[/math]. При отказе от использования таких сткрутр сложность возрастает до [math]O(n^2)[/math], так как для каждого элемента требуется проверить на нахождение в [math]\varepsilon[/math]-окрестности все остальные элементы множества.

1.7 Информационный граф

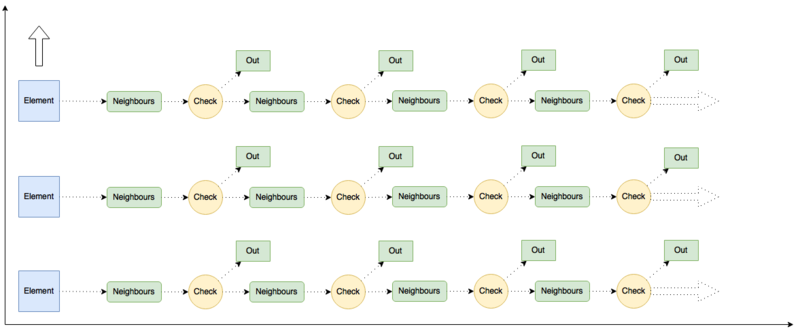
Опишем граф алгоритма как аналитически, так и в виде рисунка:

Граф алгоритма состоит из двух групп вершин, расположенных узлах двух областей двумерной размерности.

Первой группе вершин соответствует операция Neighbours. Естественно введённые координаты области таковы:

[math]i[/math] — меняется от [math]1[/math] до [math]k + f[/math], принимая все целочисленные значения, где [math]k[/math] — число результирующих кластеров, [math]f[/math] — число элементов помеченных, как шум
[math]j[/math] — меняется от [math]1[/math] до [math]t[/math], принимая все целочисленные значения, где [math]t[/math] — число вершин в кластере [math]i[/math]

Второй группе вершин соответствует операция Check. Естественно введённые координаты области аналогичны предыдущей.

Граф алгоритма DBSCAN

1.8 Ресурс параллелизма алгоритма

Так как в данном алгоритме присутствует параллелизм по данным, ширина ярусно-параллельной формы алгоритма [math]O(w)[/math], где [math]w[/math] — количество частей, на которые разбиваются все входное множество объектов [math]X[/math]. Высотой ярусно-параллельной формы алгоритма является [math]O(|H| \log |H|)[/math], где [math]|H|[/math] — максимальное количество элементов в области среди всех частей разбиения. Именно такую сложность имеет алгоритм PDBSCAN^[3], применяемый к каждой отдельной части разбиения.

1.9 Входные и выходные данные алгоритма

Входные данные: множество [math]X[/math], на котором определена функция расстояния [math]D[/math].

Объём входных данных: [math]n[/math] (размерность входящего множества)

Выходные данные: размеченное множество точек [math]X[/math], в котором каждому элементу соответствует номер его кластера.

Объём выходных данных: [math]n[/math] (размерность выходящего множества)

1.10 Свойства алгоритма

Алгоритм может определять кластера произвольной формы;
Параллельная реализация при равномерном разбиении сбалансирована по количеству и виду производимых операций;
Не требуется задание числа кластеров;
Может выделять кластеры в присутствии шума;
Не детерминирован относительно граничных точек кластеров.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

3 Литература

↑ A density-based algorithm for discovering clusters in large spatial database / M. Ester, H.-P. Kriegel, J. Sander, X. Xu // Proc. 1996 Intern. Conf. on Knowledge Discovery and Data Mining. – 1996.
↑ https://en.wikipedia.org/wiki/DBSCAN Density-based spatial clustering of applications with noise (DBSCAN)
↑ A New Scalable Parallel DBSCAN Algorithm Using the Disjoint-Set Data Structure \ Md. Mostofa Ali Patwary, Diana Palsetia, Ankit Agrawal, Wei-keng Liao, Fredrik Manne, Alok Choudhary

[1] A density-based algorithm for discovering clusters in large spatial database / M. Ester, H.-P. Kriegel, J. Sander, X. Xu // Proc. 1996 Intern. Conf. on Knowledge Discovery and Data Mining. – 1996.

[2] ttps://en.wikipedia.org/wiki/DBSCAN Density-based spatial clustering of applications with noise (DBSCAN)

[3] A New Scalable Parallel DBSCAN Algorithm Using the Disjoint-Set Data Structure \ Md. Mostofa Ali Patwary, Diana Palsetia, Ankit Agrawal, Wei-keng Liao, Fredrik Manne, Alok Choudhary

[1]

[2]

[3]

Участник:Elmon/Плотностный алгоритм кластеризации DBSCAN