Участник:Макарова Алёна/Итерационный метод решения системы линейных алгебраических уравнений GMRES (обобщенный метод минимальных невязок)

Эта работа ждет рассмотрения преподавателем Дата последней правки страницы: 16.10.2016 Авторы этой статьи считают, что задание выполнено.

Обобщенный метод минимальных невязок
Последовательный алгоритм
Последовательная сложность	[math]O(nm^2)[/math]
Объём входных данных	[math]n(n + 1)[/math]
Объём выходных данных	[math]n[/math]

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Метод минимальных невязок представляет собой итерационный метод для численного решения несимметричной системы линейных уравнений. Метод приближает решение вектором в подпространстве Крылова с минимальной невязкой. Чтобы найти этот вектор используется итерация Арнольди.

Впервые метод минимальных невязок был описан в книге Марчука и Кузнецова "Итерационные методы и квадратичные функционалы" и представлял собой геометрическую реализацию метода минимальных невязок.

Алгебраическая реализация метода минимальных невязок была предложена Саадом и Шульцем в 1986 году . С их подачи за методом закрепилась аббревиатура GMRES (обобщенный метод минимальных невязок).

1.2 Математическое описание алгоритма

Для решения системы [math]Ax = b[/math] с невырожденной матрицей [math]A[/math], выбирается начальное приближение [math]x_0[/math], затем решается редуцированная система [math]Au = r_0[/math], где [math]r_0 = b - Ax_0, x = x_0 + u[/math]. Подпространства Крылова строятся для редуцированной системы (в предположении, что [math]r_0 \neq 0[/math]).

Пусть [math]x_i = x_0 + y[/math], где [math] y \in \mathcal{K}_i [/math]. Невязка имеет вид [math]r_i = r_0 - Ay[/math], а её длина минимальна, в силу теоремы Пифагора, в том и только том случае, когда

[math] r_i \perp A\mathcal{K}_i [/math].

Таким образом, для реализации [math]i[/math]-го шага требуется опустить перпендикуляр из вектора [math]r_0[/math] на подпространство [math]A\mathcal{K}_i[/math]. Проще всего это сделать, если в данном подпространстве уже найден ортогональный базис. .

1.2.1 Геометрическая реализация

Геометрическая реализация метода минимальных невязок заключается в построении последовательности векторов [math]q_1, q_2,...[/math] таким образом, что [math]q_1, q_2,.., q_i[/math] дают базис в подпространстве Крылова [math]\mathcal{K}_i[/math] и при этом вектора [math]p_1 = Aq_1, ..., p_i = Aq_i[/math] образуют ортогональный базис в подпространстве [math]A\mathcal{K}_i[/math]. Вектор [math]q_{i+1} \notin \mathcal{K}_i[/math] должен обладать следующими свойствами:

[math] q_{i+1} \in \mathcal{K}_{i+1}, p_{i+1} = Aq_{i+1} \perp A\mathcal{K}_i [/math].

Его можно получить с помощью процесса ортогонализации, применённого к вектору [math]p = Aq[/math], где [math]q = Aq_i[/math]. В геометрической реализации необходимо хранить две системы векторов: [math]q_1, ..., q_i[/math] и [math]p_1, ..., p_i[/math].

1.2.2 Алгебраическая реализация

Алгебраическая реализация метода минимальных невязок использует лишь одну систему векторов, образующих ортогональные базисы в подпространствах [math]\mathcal{K}_i[/math].

[math]q_1 = r_0/||r_0||_2[/math]. Чтобы получить ортонормированный базис [math]q_1, ..., q_{i+1}[/math] в [math]\mathcal{K}_{i+1} = \mathcal{K}_{i+1}(r_0, A)[/math], проводим ортогонализацию вектора [math]Aq_i[/math] к векторам [math]q_1, ..., q_i[/math]. Если [math]Q_i \equiv [q_1, ..., q_i] \in \mathbb{C}^{n*i}[/math], то получим

[math] AQ_i = Q_{i+1}\hat{H_i}, \hat{H_i}= \begin{bmatrix} H_i \\ 0 ... 0 & h_{i+1 i} \end{bmatrix}, [/math]

где [math]H_i[/math] - верхняя хессенбергова матрица порядка [math]i[/math].

Далее рассмотрим [math]QR[/math]-разложение прямоугольной матрицы [math]\hat{H_i}[/math]:

[math] \hat{H_i} = U_iR_i, R_i \in \mathbb{C}^{i*i} [/math].

Тогда минимум невязки [math]||r_0 - AQ_iy||_2[/math] по всем [math]y[/math] будет достигаться в том случае, если [math]y = y_i[/math] удовлетворяет уравнению

[math] R_iy_i = z_i \equiv ||r_0||_2U^T_ie_1, e_1 = \begin{bmatrix} 1 0 ... 0 \end{bmatrix}^T, [/math].

Матрица [math]R_i[/math] невырожденная, следовательно,

[math] x_i = x_0 + Q_iy_i = x_0 + Q_iR_i^{-1}z_i [/math].

1.2.3 Сходимость метода

Метод минимизации невязок на подпространствах Крылова за конечное число итераций приводит к точному решению и по этой причине является прямым методом. Но чаще его рассматривают как итерационный метод - с типичными для итерационных методов оценками сходимости. Идея заключается в том, что спустя некоторое количество итераций, полученное приближение уже является хорошей оценкой ответа.

Но об этом не верно говорить в общем. Согласно теореме (Greenbaum, Pták and Strakoš), для каждой монотонной последовательности [math] a_1,..., a_{m-1}, a_m = 0 [/math], найдётся матрица [math]A[/math] такая что [math]||r_n|| = a_n[/math] для всех [math]n[/math], где [math]r_n[/math] невязка, определенная ранее.

На практике для матрицы порядка [math]n[/math] число шагов может оказаться равным [math]n[/math], а норма невязки может оставаться равной норме начальной невязки на всех шагах, кроме последнего.

Пример

[math] \begin{bmatrix} 0 1 & ... \\ 0 0 1 & ... \\...\\... & 01 \\1 & ... \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\...\\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\...\\ 0 \\ 1 \end{bmatrix} [/math]

Если [math] x_0 = 0 [/math], то [math] r_0 = b[/math]. Подпространства Крылова получаются такие:

[math] \mathcal{K}_i = span \{ e_n, e_{n-1}, ..., e_{n-i+1}\}, i \le i \le n [/math]

Точное решение системы имеет вид [math]x = e_1[/math], а на итерациях получаются следующие векторы:

[math] x_0 = x_1 = ... = x_{n-1} = 0, x_n = e_1 [/math].

Для получения оценок требуются дополнительные предположения относительно матрицы коэффициентов.

1.2.3.1 Сходимость для положительно определенной матрицы

Если матрица [math]A[/math] положительно определена, то

[math] \|r_n\| \leq \left( 1-\frac{\lambda_{\mathrm{min}}^2(1/2(A^T + A))}{ \lambda_{\mathrm{max}}(A^T A)} \right)^{n/2} \|r_0\|, [/math],

где [math]\lambda_{\mathrm{min}}(M)[/math] и [math]\lambda_{\mathrm{max}}(M)[/math] обозначают наибольшее и наименьшее собственное значение матрицы [math]M[/math], соответственно.

1.2.3.2 Сходимость для симметричной матрицы

Если матрица [math]A[/math] является симметрично и положительно определена, тогда

[math] \|r_n\| \leq \left( \frac{\kappa_2(A)^2-1}{\kappa_2(A)^2} \right)^{n/2} \|r_0\| [/math],

где [math]\kappa_2(A)[/math] число обусловленности матрицы [math]A[/math] в Евклидовой норме.

Если не требовать положительной определённости

[math] \|r_n\| \le \inf_{p \in P_n} \|p(A)\| \le \kappa_2(V) \inf_{p \in P_n} \max_{\lambda \in \sigma(A)} |p(\lambda)| \|r_0\|, \, [/math]

где [math]P_n[/math] обозначает множество полиномов степени не выше [math]n[/math] и [math]p(0) = 1[/math], матрица [math]V[/math] появляется из спектрального разложения матрицы [math]A[/math] и [math]\sigma(A)[/math] - спектр матрицы [math]A[/math]. Грубо говоря, это означает, что быстрая сходимость имеет место, когда собственные значения матрицы [math]A[/math] невелики и [math]A[/math] не сильно отклоняется от нормальной матрицы.

Все эти неравенства связаны с невязкой вместо фактической ошибки, т.е. расстоянием между текущей итерацией и точным решением.

1.3 Вычислительное ядро алгоритма

Самой трудоёмкой процедурой в методе является [math]QR[/math]-разложение [math]\hat{H_i}[/math]. В общем случае требуется [math]\mathcal{O}(i^3)[/math] арифметических операций, однако то, что [math]\hat{H_i}[/math] является хессенберговой матрицей, позволяет сократить требуемый объём до [math]\mathcal{O}(i^2)[/math] действий.

1.4 Макроструктура алгоритма

Алгоритм начинается с выбора начального приближения [math]x_0[/math]. Далее для [math]i = 1,2 ..[/math]

1. Вычисляем матрицу [math]\hat{H_i}[/math].

2. Находим её [math]QR[/math]-разложение: [math]\hat{H_i} = U_iR_i[/math].

3. Решаем систему [math]R_iy_i = U^T_ie_1[/math].

4. Находим приближение [math]x_i = x_0 + Q_iy_i[/math].

Алгоритм завершается, когда норма вектора невязки становится достаточно малой. При большом числе итераций вычислительные затраты и требуемая для хранения векторов [math]p_i[/math] память могу оказаться чрезмерно большими. В таких случаях применяют алгоритм с перезапусками (restart): задают максимальную допустимую размерность [math]K[/math] пространств Крылова [math]\mathcal{K}_i[/math], и если точность не достигнута, берут полученное приближение в качестве нового начального приближения [math]x^0_{new} = x_K[/math].

1.5 Схема реализации последовательного алгоритма

1.6 Последовательная сложность алгоритма

Будем предполагать, что матрица решаемой СЛАУ является разреженной. Пусть несимметричная матрица [math]A[/math] имеет симметричный портрет и число ненулевых элементов в нижнем(верхнем) треугольнике равно [math]k[/math].

При [math] m \lt \lt n [/math] можно говорить, что один GMRES-цикл имеет сложность [math]\mathcal{O}(nm^2)[/math].

Требования по памяти с учетом [math]1 \lt m \lt \lt n[/math] и [math]k \lt \lt n[/math] составляют [math]\mathcal{O}(mn)[/math]..

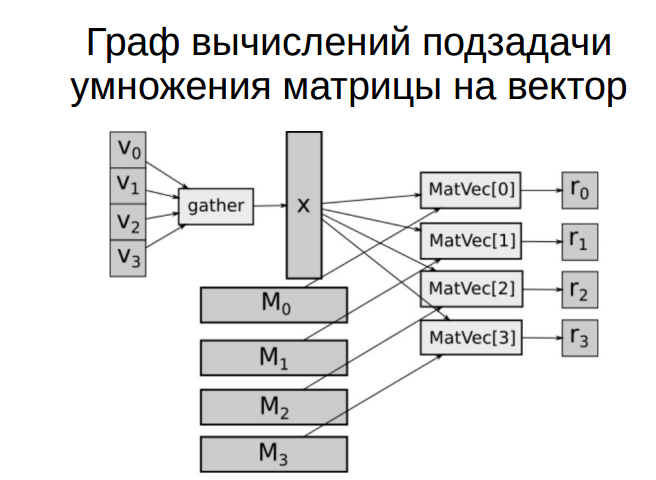
1.7 Информационный граф

1.8 Ресурс параллелизма алгоритма

В вычислительной схеме присутствуют два интенсивных в вычислительном плане этапа:

1. Умножение матрицы СЛАУ на вектор (для нахождения невязок).

Для нахождения матрично-векторных произведений при вычислении невязок матрича должна быть подвергнута декомпозиции на строчные блоки.

2. Нахождение скалярных произведений векторов (при построении ортонормального базиса подпространства Крылова).

Для наиболее эффективного вычисления скалярных проихведений и линейных комбинаций векоров базиса каждый из векторов [math]p_i[/math] должен быть разбит на блоки равного размера по числу процессоров.

Кроме того, на хранение векторов базиса приходится бОльшая часть затрат памяти.

1.9 Входные и выходные данные алгоритма

Входные данные: Обязательные параметры:

[math]A[/math] - квадратная матрица (n x n).

[math]b[/math] - вектор правой части (n x 1).

Вариативно:

[math]x_0[/math] - начальное приближение (может не передаваться и быть всегда нулевым).

[math]\epsilon[/math] - погрешность (может не передаваться и быть заданным по умолчанию, обычно равна 1e-6).

Максимальное число итераций.

Выходные данные: [math]x^*[/math] - решение системы [math]Ax = b[/math]

1.10 Свойства алгоритма

1. Рассматриваемый алгоритм предназначен для решения невырожденных линейных систем большой размерности. При этом симметрия и положительная определенность матрицы не предполагается.

2. Для систем с разряженной матрицей алгоритм требует гораздо меньшей вычислительной мощности.

3. Особенностью метода является то, что с целью экономии памяти выбирается некоторая размерность Крылова [math]m[/math], и после того как [math]m[/math] базисных векторов построены, решение уточняется.

4. Одной из важных практических особенностей метода является то, что на первых итерациях метод сходится гораздо быстрее, чем асимптотически. Для ускорения сходимости метода минимальных невязок целесообразно время о времени использовать один шаг двух-шагового метода минимальных невязок.

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

Алгоритм GMRES достаточно популярен и его реализацию можно найти во многих пакетах прикладных программ.

Пример: MATLAB

   

Итерационный метод минимизации обобщенной невязки реализован в системе MATLAB. Для этого используется функция gmres:

gmres (А, В. restart) — возвращает решение X СЛУ А*Х=В. А —квадратная матрица. Функция gmres начинает итерации от начальной оценки, представляющей собой вектор размера и, состоящий из нулей. Итерации производятся либо до сходимости к решению, либо до появления ошибки, либо до достижения максимального числа итераций. Сходимость достигается, когда относительный остаток norm(B-A*X)/norm(B) меньше или равен заданной погрешности (по умолчанию 1е-6). Максимальное число итераций — минимум из n:restart и 10. Функция gmres (...) имеет и ряд других форм записи, аналогичных описанным для функции bieg(...).  

» gmres(A.B)

GMRES(4) converged at Iteration 1(4) to a solution with relative residual le-016

ans =

1.0000

2.0000

3.0000

4.0000

Список пакетов, в которых присутствует реализация метод минимизации обобщенной невязки:

1.ATLAS (Automatically Tuned Linear Algebra Software) – оптимизированная библиотека, включающая реализацию процедур BLAS и часть функциональности LAPACK;

2.AZTEC – библиотека параллельных подпрограмм для решения больших систем линейных алгебраических уравнений с разреженными матрицами;

3.BLAS (Basic Linear Algebra Subprograms) – библиотека высококачественных процедур, «строительными блоками» для которых являются вектора, матрицы или их части. Уровень 1 BLAS используется для выполнения операций вектор-вектор, уровень 2 :BLAS – для выполнения матрично-векторных операций, наконец, уровень 3 BLAS – для выполнения матрично-матричных операций. Поскольку программы BLAS являются эффективными, переносимыми и легко доступными, они используются как базовые компоненты для развития высококачественного программного обеспечения для задач линейной алгебры. Так были созданы широко известные пакеты LINPACK, EISPACK, которые затем были перекрыты пакетом LAPACK, получившим большое распространение. Перечисленные пакеты разработаны на языке Fortran;

4.BLACS (Basic Linear Algebra Communication Subprograms) – набор базовых коммуникационных процедур линейной алгебры, созданных для линейной алгебры. Вычислительная модель состоит из одномерной или двумерной решетки процессов, где каждый процесссодержит часть матрицы или вектора. BLACS используется как коммуникационный слой проекта ScaLAPACK, который переносит библиотеку LAPACK на машины с распределенной памятью;

5.BlockSolve95 – параллельная библиотека для решения разреженных систем линейных уравнений;

6.BPKIT2 – пакет блочных способов предобусловливания, ориентированных на разреженные матрицы;

7.CAPSS – пакет для параллельного решения разреженных линейных систем;

8.CXML (The Compaq Extended Math Library) – расширенная математическая библиотека, включающая в себя часть функциональности BLAS, LAPACK, Direct Sparse Solvers и Iterative-solvers;

9.Direct Sparse Solvers – пакет программ для решения разреженных систем прямыми методами;

10.EISPACK (Eigensystem Package) – пакет программ решения алгебраической проблемы собственных значений;

11.Expokit – пакет программ для решения не больших СЛАУ с плотной матрицей и больших разреженных систем;

12.ILUPACK – библиотке, содержащая способы предобусловливания, ориентированная на разреженные СЛАУ. Пакет включает реализацию процедур BLAS, SPARSEKIT. Реализована на языке С и Fortran;

13.IML++ (Iterative Methods Library) – библиотека итерационных методов решения разреженных СЛАУ, позволяющая использовать несколько простых способов предобусловливания. Пакет включает часть BLAS и MV;

14.Intel MKL (Intel Math Kernel Library) включает несколько стандартных библиотек для высокопроизводительных системах (BLAS, LAPACK и FFTPACK – подпрограммы быстрого преобразования Фурье);

15.IOMDRV – пакет подпрограмм для решения симметричных и несимметричных линейных систем методами крыловских подпространств;

16.Iterative-solvers – пакет подпрограмм решения разреженных систем итерационными методами;

17.ITL (Iterative Template Library) – библиотека программ итерационных методов и способов предобусловливания, являющаяся составной частью MTL.

18.ITPACK (Iterative Package) – пакет программ для решения разреженных систем итерационными методами;

19.ITSOL (The New Sparskit Preconditionning Module) – пакет, содержащий способы предобусловливания, ориентированные на разреженные матрицы. Является составной частью пакета SPARSKIT;

20.JAMA/C++ – библиотека для решения СЛАУ прямыми методами;

21.LAPACK (Linear Algebra Package) – набор реализаций «продвинутых» методов линейной алгебры. LAPACK содержит процедуры для решения систем линейных уравнений, задач нахождения собственных значений и факторизации матриц. Обрабатываются заполненные и ленточные матрицы, но не разреженные матрицы общего вида. Во всех случаях можно обрабатывать действительные и комплексные матрицы с одиночной и удвоенной точностью. Процедуры LAPACK построены таким образом, чтобы как можно больше вычислений выполнялось с помощью обращений к BLAS с использованием всех его трех уровней. Вследствие крупнозернистости операций уровня 3 BLAS, их использование обеспечивает высокую эффективность на многих высокопроизводительных компьютерах, в частности, если производителем создана специализированная реализация. ScaLAPACK является успешным результатом переноса пакета LAPACK на системы с передачей сообщений. Но в таких системах необходимы процедуры, обеспечивающие обмен данными между взаимодействующими процессами. Для этого в ScaLAPACK используется библиотека BLACS;

22.Laspack – пакет программ для решения разреженных систем итерационными методами;

23.LGSOLV – библиотека для решения СЛАУ прямыми методами;

24.LINPACK (Linear Package) – пакет программ решения систем линейных алгебраических уравнений и линейной задачи наименьших квадратов прямыми методами;

25.LinPar – пакет предназначенный для решения плохообусловленных СЛАУ, включая прямоугольные. Если для решения задачи необходимо предобусловливание СЛАУ, то оно выполняется отдельно и методы применяются к уже предобусловленной системе. Соответственно, по окончании процесса решения найденный вектор должен быть пересчитан согласно выполненному предобусловливанию. В схемы методов эти процедуры не включаются;

26.MET (Matrix Expression Templates) – реализованная на языке C++ программа для инженеров и научных работников;

27.MINOS – пакет подпрограмм решения больших разреженных задач линейного и нелинейного программирования;

28.MTL (The Matrix Template Library) – реализованная на языке C++ библиотека базовых операций линейной алгебры, позволяющая решать СЛАУ с разреженными матрицами итерационными методами с предобусловлмванием, за счет включенного пакета ITL;

29.MV++ – небольшая библиотека, содержащая базовые операции линейной алгебры. Данный пакет часто является составной частью более крупных и высокопроизводительных библиотек;

30.ParPre – пакет параллельных версий способов предобусловливания, ориентированных на разреженные матрицы, являющийся составной частью PETs;

31.Parallel Algorithms Project – пакет параллельных версий итерационных методов Крыловского типа для решения разреженных систем;

32.PASVA – пакет подпрограмм решения разреженных систем с блочно-двухдиагональной структурой;

33.PBLAS – Параллельные версии базовых процедур линейной алгебры (BLAS) ;

34.PCGPAK (Preconditioned Conjugate Gradient PAcKage) – пакет программ для решения симметричных и несимметричных разреженных линейных систем методом сопряженных градиентов;

35.PIM (The Parallel Iterative Methods) – набор процедур на Фортран-77, реализующих параллельные версии различных итеративных методов решения разреженных систем линейных уравнений;

36.PSparselib (A Portable Library of Parallel Sparse Iterative Solvers) – библиотека параллельных итерационных методов для разреженных линейных систем;

37.PSPASES (Parallel Sparse Symmetric Direct Solver) – библиотека параллельных версий прямых методов для решения симметричных линейных систем;

38.RALAPACK – пакет подпрограмм для различных операций с разреженными матрицами;

39.ScaLAPACK (Scalable LAPACK) – параллельная версия LAPACK. Широкий набор подпрограмм для решения стандартных задач линейной алгебры;

40.SIRSM – пакет подпрограмм для решения разреженных несимметричных линейных систем;

41.Software Iterative Methods: GMRESR and BiCGstab(ell) – пакет прогамм решения больших разреженных систем с несимметричной матрицей;

42.SPAI (Sparse Approximate Inverse Preconditioner) – пакет способов предобусловливания, ориентированных на разреженные матрицы;

43.SPARKS – пакет подпрограмм для решения разреженных линейных систем в полунеявных методах Рунге-Кутта численного интегрирования систем обыкновенных дифференциальных уравнений;

44.SparseLib++ – библиотка, реализованная на языке C++, позволяющая решать разреженные СЛАУ итерационными методами с предобусловливанием. Включает часть процедур BLAS и IML;

45.SPARSKIT – мощный пакет для решения разреженных СЛАУ итерационными методами с предобусловливанием. Библиотека реализованна на языке Fortran;

46.SPARSPAK (Sparsee Iinear Equations Package) – пакет программ решения разреженных систем линейных алгебраических уравнений с симметричными положительно определенными матрицами;

47.SPLIB – библиотека, позволяющая решать СЛАУ с разреженной матрицей итерационными методами с предобусловливанием, реализованная на языке Fortran;

48.SPLP (Sparse Linear Programming Subprogram) – пакет программ решения задач линейного программирования;

49.SPOOLES – библиотека для решения СЛАУ с разреженной матрицей прямыми методами;

50.SSLES – пакет подпрограмм для решения разреженных несимметричных линейных систем;

51.TCHLIB – пакет подпрограмм для решения симметричных и несимметричных линейных систем методом Чебышева;

52.TNT (Template Numerical Toolkit) – библиотека базовых операций линейной алгебры, ориентированная на разреженные матрицы. Библиотека разработана на языке Fortran;

53.WSMP (Watson Sparse Matrix Package) – пакет программ решения разреженных систем линейных алгебраических уравнений;

54.XMP – пакет подпрограмм для решения задач линейного программирования;

55.YI2M – комплекс программ решения разреженных систем;