Самоорганизующаяся карта Кохонена (алгоритм кластеризации)

Авторы проекта: Авторы страницы Быковец Евгений Владимирович (620 группа) и Ворона Игорь Игоревич (620 группа) Быковец Е.В.: 1.1,1.2,1.3,1.4,1.5,2.7 Ворона И.И.: 1.6,1.7,1.8,1.9,1.10

Алгоритм кластеризации, основанный на самоорганизующихся сетях Кохонена
Последовательный алгоритм
Последовательная сложность	[math]O(n^3)[/math]
Объём входных данных	[math]\frac{n (n + 1)}{2}[/math]
Объём выходных данных	[math]\frac{n (n + 1)}{2}[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(n)[/math]
Ширина ярусно-параллельной формы	[math]O(n^2)[/math]

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Cамоорганизующаяся карта Кохонена (Self-Organizing Map, SOM) представляет из себя вычислительный метод, предназначенный для задач, в первую очередь, кластеризации и визуализации, а также анализа данных из пространств высокой размерности (иначе, многомерных данных), полученных экспериментально. Методы был предложен Туево Кохоненом (1982). Прародителями модели самоорганизующейся сети Кохонена были ранние нейросетевые модели (в частности, модель ассоциативной памяти и модель адаптивного обучения).

Целью применения данного метода является поиск скрытых закономерностей в данных, основываясь на снижении размерности исходного пространства в пространство меньшей размерности (на практике чаще всего используется двумерное, по причине, в частности, удобной визуализации). При этом топология исходного пространства остается той же самой. В результате обучения данной модели получается решетка, состоящая из обученных нейронов, она же и называется "картой" исходного пространства.

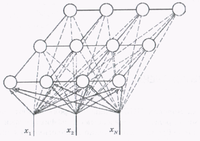
Архитектура самоорганизующейся карты Кохонена следующая: имеется два слоя - входной слой (распределительный) нейроноы и выходной слой (слой Кохонена) нейронов, при этом нейроны второго слоя расположены в виде двумерной решетки (обычно сетка либо квадратная, либо шестиугольная, об этом далее), так, что каждый нейрон из первого слоя соединен с каждым нейроном второго слоя (см. рис. 1)

Рис. 1. Общая структура карты Кохонена

Количество нейронов входного слоя равно размерности исходного пространства. Чаще нейроны слоя Кохонена принято называть кластерными элементами. Более точно, их количество определяет количество кластеров, на которые карта может разбить данные, которые поданы на распределительный слой. Чем больше кластерных элементов, тем более гранулярная кластеризация. Как уже было сказано, топология слоя Кохонена может быть представлена либо виде четырехугольной сетки, либо в виде шестиугольной сетки. Второй вариант более привлекателен в силу того, что расстояния для каждого нерона до каждого соседнего с ним нейрона одинаковые. Более наглядно это представлено на рисунках (cм. рис. 2а, рис. 2б)

Рис. 2а.Четырехугольная решетка слоя Кохонена

Рис. 2б.Шестиугольная решетка слоя Кохонена

Каждый нейрон выходного слоя определяется вектором весов (размерность вектора - есть разность входного пространства) и упорядоченной парой : [math](x,y)[/math], определяющую позицию нейрона на карте Кохонена.

Принцип обучения сети заключается в следующем: для каждого входного вектора определяется нейрон-победитель из слоя Кохонена, после чего у нейрона-победителя и некоторого количества его соседей корректируются веса. Процедура повторяется для каждого входного вектора из обучающей выборки.

Сеть, с предложенной архитектурой, обучается на обучающей выборке, обучение заключается в корректировке весов нейронов в слое Кохонена. После того, как сеть обучена она начинает свою работу, относя каждый нейрон из тестовой выборки к тому или иному кластеру.

1.2 Математическое описание алгоритма

1.2.1 Используемые обозначения

[math]t[/math] - номер итерации,

[math]n[/math] - размерность исходного пространства,

[math] \chi \in R^n[/math] - обучающая выборка,

[math] \Phi \in R^n [/math] - тестовая выборка,

[math] N = |\chi|[/math] - размер обучающей выборки,

[math] K = |\Phi|[/math] - размер тестовой выборки,

[math] a [/math] - высота слоя Кохонена,

[math] b [/math] - ширина слоя Кохонена,

[math] M = a \times b [/math] - общее количество нейронов в слое Кохонена,

[math] ne_j, j=1,...M [/math] - нейрон с индексом [math]j[/math],

[math]\vec{x}^{(i)}(t) = (x_1^{(i)}(t),...,x_n^{(i)}(t)), i=1,..,N[/math] - [math]i[/math]-й вектор, подлежайщий кластеризации,

[math]\vec{w}^{(j)}(t) = (w_1^{(j)}(t),...,w_n^{(j)}(t)), j = 1,..,M[/math] - вектор весовых коэффициентов для [math]j[/math]-го нейрона,

[math] r_k[/math] - положение [math]k[/math]-го нейрона в топологии карты, то есть [math](i_k,j_k)[/math],

[math] h_{ij}(t)[/math] - функция соседства между нейронами с индексами [math]i[/math] и [math]j[/math] на итерации t,

[math] h(d,t) [/math] - функция от расстояния между нейронами,

[math] \alpha(t)[/math] - скорость обучения сети,

[math] \sigma(t) [/math] - функция, уменьшающая количество соседей с при увеличении итерации (монотонно убывающий),

[math] T [/math] - максимальное число итераций алгоритма обучения - может быть задано фиксировано, либо же равно мощности обучающей выборки, то есть [math] N [/math].

1.2.2 Алгоритм обучения

Шаг №0. Определить значение параметров алгоритма: используемые метрики, функции [math]\alpha(t) [/math], [math]\sigma(t) [/math], [math]t:= 0 [/math]

Шаг №1. Инициализировать векторы начальных весов нейронов [math] \vec{w}^{(j)}(0) \forall j=1,..,M[/math]. Подробнее о стратегии начальной инициализации далее.

шаг №2. Если есть еще элементы в обучающей выборке, вытащить случайным образом (например, индекс [math]i[/math] - может быть реализацией случайной величины из равномерного дискретного распределения на [math] [0,N] [/math]) входной вектор [math]\vec{x}^{(i)}(t), N:=N-1, \chi = \chi \setminus \vec{x}^{(i)}(t)[/math], в противном случае алгоритм завершает свою работу

шаг №3. Для [math]\vec{x}^{(i)}(t)[/math] и [math] \vec{w}^{(j)}(t) \forall j=1,..,M[/math] найти [math] = \rho(\vec{x}^{(i)}(t), \vec{w}^{(j)}(t)) = || \vec{x}^{(i)}(t) - \vec{w}^{(j)}(t)||^2 [/math].

шаг №4. Находим нейрон-победитель [math]ne_c[/math], [math] c = \arg \min_{\forall j \in \{1, \dots, M\}} \rho(\vec{x}^{(i)}(t), \vec{w}^{(j)}(t))[/math], который лежит ближе к текущему объекту [math]\vec{x}^{(i)}(t)[/math] по рассматриваемой метрике [math] || \circ || [/math].

шаг №5. Для всех нейронов [math] ne_{j} [/math] выполнить пересчет весовых векторов: [math] \vec{w}^{(j)}(t+1) := \vec{w}^{(j)}(t) +\alpha(t)h_{ci}(t)[\vec{x}^{(i)}(t) - \vec{w}^{(j)}(t)][/math].

шаг №6. [math]t := t+1 [/math]

шаг №7. Перейти к шагу 2.

1.2.3 Настройка алгоритма

В этом разделе опишем более подробно настраиваемые аспекты алгоритма.

1.2.3.1 Выбор начального приближения для [math]\vec{w}^{j}(0) \forall j=1,\dots,M[/math]

Во-первых, инициализацию можно проводить объектами из обучающей выборки, то есть выбрав для каждого весового вектора некоторый элемент из обучающий выборки и установить значения весовых компонент равными компонентам выбранного вектора. Плюсом такого подхода является то, что вектора весов изначально находятся в том регионе, где и объекты из выборки, то есть требуется меньше итераций на этапе настройки.

Во-вторых, инициализацию весов можно проводить какими-то случайными значениями. Например можно взять нескорое распределение, пусть равномерное или нормальное, и для каждой сгенерировать псевдослучайное число из выбранного распределения, то есть [math] w_i^{(j)} \sim \mathbf P [/math], где [math] \mathbf P [/math] - это заданное распределение. Плюсом данного подхода является простота однако, "настройка" в данном случае может быть долгой.

В-третьих, можно использовать линейную инициализацию, то есть весовые вектора имеют значения векторов из подпространства, натянутого на два главных собственными вектора пространства исходного набора данных, при этом упорядоченным образом. Это наиболее практичный способ.

1.2.3.2 Выбор скорости обучения сети

Функцию скорости обучения сети [math]\alpha(t)[/math] можно выбрать, например, следующим образом:

Самый простой способ: [math]\alpha(t) := \frac{A}{B+t}[/math], где [math]A = const, B = const [/math]

Экспоненциальная скорость обучения: [math]\alpha(t) := \alpha_0 e^{ -\frac{t}{\lambda}}, \lambda \in (0, 1), \lambda = const, \alpha_0 = const[/math]

Показательная скорость обучения: [math]\alpha(t) := \lambda^{\frac{t}{T}}, \lambda \in (0, 1), \lambda = const[/math]

1.2.3.3 Выбор функции соседства между нейронами

Обычно полагают [math] h_{cj}(t) := \alpha(t) h(d,t) [/math], где [math] d = || ne_c - ne_j ||, c [/math] -индекс нейрона победителя, при этом:

[math] h(d,t) = \begin{cases}const, d\leq \sigma(t) \\0, d \gt \sigma(t) \end{cases}[/math]

[math] h(d,t) = e ^{-\frac{d^2}{2(\sigma(t)^2)}}[/math], где [math]\sigma(t)[/math] - это некоторый сомножитель, уменьшающий количество соседей, которые будут подвержены корректировке весов с увеличением итераций, эта функция монотонно убывает.

Функция [math] \sigma(t) [/math] также является параметром алгоритма. Возможная функциональная зависимость для нее: [math]\sigma(t) = \frac{\sigma_0}{1 + \frac{t}{T}}[/math].

Стоит отметить, что имеется много других эвристических мер сходств которые присваивают ненулевые веса внутри некоторого радиуса, это позволяет производить вычисления не для всех соседей.

1.2.4 Алгоритм работы карты

шаг 0. Пока есть вектора в тестовой выборке извлечь (последовательно), [math]\vec{x}^{(i)}, K:=K-1, \Phi = \Phi \setminus \vec{x}^{(i)}[/math], в противном случае алгоритм завершает свою работу.

шаг 1. Для [math]\vec{x}^{(i)}[/math] и [math] \vec{w}^{(j)} \forall j=1,..,M[/math] найти [math] \rho(\vec{x}^{(i)}, \vec{w}^{(j)}) = || \vec{x}^{(i)} - \vec{w}^{(j)}||^2 [/math].

шаг 2. Находим нейрон-победитель [math]ne_c[/math], [math] c = \arg \min_{\forall j \in \{1, \dots, L\}} \rho(\vec{x}^{(i)}, \vec{w}^{(j)})[/math], который лежит ближе к текущему объекту [math]\vec{x}^{(i)}[/math] по рассматриваемой метрике [math] || \circ || [/math] и относим [math]\vec{x}^{(i)} [/math] к кластеру, соответствующему нейрону [math]ne_c[/math].

шаг 3. Переход к шагу 0.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма обучения составляет (соответсвенно, пункты 3,4,5 алгоритма обучения):

• подсчет расстояний между входным вектором и всеми нейронами:

Для [math]\vec{x}^{(i)}(t)[/math] и [math] \vec{w}^{(j)}(t) \forall j=1,..,M[/math] найти [math] = \rho(\vec{x}^{(i)}(t), \vec{w}^{(j)}(t)) = || \vec{x}^{(i)}(t) - \vec{w}^{(j)}(t)||^2 [/math].

• Поиск минимума между всеми найденными расстояниями для нахождения нейрона-победителя:

Находим нейрон-победитель [math]ne_c[/math], [math] c = \arg \min_{\forall j \in \{1, \dots, L\}} \rho(\vec{x}^{(i)}(t), \vec{w}^{(j)}(t))[/math], который лежит ближе к текущему объекту [math]\vec{x}^{(i)}(t)[/math] по рассматриваемой метрике [math] || \circ || [/math].

• Корректировка весовых векторов: сюда же входит поиск расстояний между всеми нейронами в рамках заданной топологии, а также вычисление функции соседства:

Для всех нейронов [math] ne_{j} [/math] выполнить пересчет весовых векторов: [math] \vec{w}^{(j)}(t+1) := \vec{w}^{(j)}(t) +\alpha(t)h_{ci}(t)[\vec{x}^{(i)}(t) - \vec{w}^{(j)}(t)][/math].

Вычислительное ядро алгоритма работы составляет (соответсвенно, пункты 1, 2 алгоритма работы):

• подсчет расстояний между входным вектором и всеми нейронами:

Для [math]\vec{x}^{(i)}[/math] и [math] \vec{w}^{(j)} \forall j=1,..,M[/math] найти [math] \rho(\vec{x}^{(i)}, \vec{w}^{(j)}) = || \vec{x}^{(i)} - \vec{w}^{(j)}||^2 [/math].

• Поиск минимума между всеми найденными расстояниями для нахождения нейрона-победителя:

Находим нейрон-победитель [math]ne_c[/math], [math] c = \arg \min_{\forall j \in \{1, \dots, L\}} \rho(\vec{x}^{(i)}, \vec{w}^{(j)})[/math], который лежит ближе к текущему объекту [math]\vec{x}^{(i)}[/math] по рассматриваемой метрике [math] || \circ || [/math] и относим [math]\vec{x}^{(i)} [/math] к кластеру, соответствующему нейрону [math]ne_c[/math].

1.4 Макроструктура алгоритма

В алгоритме обучения можно выделить 4 макрофазы:

• Начальная инициализация всех весов: построение матрицы [math] \mathbf{ W(0)} \in \mathbf {R^{N \times M}} [/math], столбцами которой являются весовые вектора всех нейронов.

• Выполнение следующих фаз [math] \mathbf T [/math] раз:
  • Вычисление вектора расстояний [math] \mathbf D \in \mathbf {R^M} [/math], в котором хранятся вектора расстояний от вектора [math] \mathbf X [/math] до векторов матрицы [math] \mathbf {W(t)} [/math].
  • Нахождение индекса минимума в векторе [math] \mathbf D [/math] - индекса нейрона победителя;
  • Корректировка всех весов: получение матрицы [math] \mathbf {W(t+1)} [/math]

В алгоритме работы алгоритма можно выделить две макрофазы:

• Выполнение следующих фаз [math] \mathbf K [/math] раз:
  • Вычисление вектора расстояний [math] \mathbf D \in \mathbf {R^M} [/math], в котором хранятся вектора расстояний от вектора [math] \mathbf X [/math] до векторов матрицы [math] \mathbf {W} [/math].
  • Нахождение индекса минимума в векторе [math] \mathbf D [/math] - индекса нейрона победителя и определение входного вектора в кластер, соответсвующий нейрону-победителю;

Также можно выделить математические операции, используемые в вышеприведенных:

• [math]\vec{x}^{T} \vec{y}[/math] - скалярное произведение вектров;
• [math]\vec{x} + \vec{y}[/math] - сложение двух векторов;
• [math]\lambda \vec{x}[/math] - умножение вектора на скаляр;
• [math]\min_i x_i[/math] - поиск минимального элемента в векторе [math]\vec{x}[/math];
• Вычисление функции соседства [math] h_{ci}(t) [/math]

1.5 Схема реализации последовательного алгоритма

Схему реализации последовательного алгоритма обучения запишем в виде псевдокода:

[math]SetAlgorithmParameters()[/math]

[math]CalculateDistancesBetweenNeuronsInEuclidianPlane()[/math]

[math]W = SetNeuronWeightsVector()[/math]

FOR [math]t=1[/math] to [math]T[/math] do

[math]x = ChooseInputVector()[/math]

[math]D = InitialiseDistancesVector()[/math]

FOR [math]n = 1[/math] to [math]M[/math] do

[math]d= CalculateDistanseBetweenInputVectorAndNeuronWeightsVector(x,n)[/math]

[math]PutCalculatedDistanceToDistancesVector(D, d)[/math]

ENDFOR

[math]ne_c = FindNeuronWinner(D)[/math]

FOR [math]n = 1[/math] to [math]M[/math] do

[math]CorrectNeuronsWeightsVector(W)[/math]

ENDFOR

ENDFOR

ENDFOR

Схему реализации последовательного алгоритма обучения запишем в виде псевдокода:

FOR [math]t=1[/math] to [math]T[/math] do

[math]x = ChooseInputVector()[/math]

[math]D = InitialiseDistancesVector()[/math]

FOR [math]n = 1[/math] to [math]K[/math] do

[math]d= CalculateDistanseBetweenInputVectorAndNeuronWeightsVector(x,n)[/math]

[math]PutCalculatedDistanceToDistancesVector(D, d)[/math]

ENDFOR

[math]ne_c = FindNeuronWinner(D)[/math]

[math]DefineInputVectorToCluster()[/math]

ENDFOR

ENDFOR

Дадим комментарии по некоторым функциям: [math]SetAlgorithmParameters()[/math] - установка параметров алгоритма проводится исследователем для увеличения/уменьшения гранулярности кластеризации;

[math]CalculateDistancesBetweenNeuronsInEuclidianPlane()[/math] - вычисление матрицы расстояний между всеми нейронами в Евклидовой плоскости, в соответствии с их расположением в слое Кохонена - эта информация потребуется [math]CorrectNeuronsWeightsVector(W)[/math].

[math]W = SetNeuronWeightsVector()[/math] - установка векторов веса нейронов (стратегии инициализации были рассмотрены выше: случайным образом, значениями из обучающей выборки, с помощью значений из пространства векторов, натянутого на главные компоненты);

[math]x = ChooseInputVector()[/math] - выбор входного вектора из выборки (стратегия выбора также было рассмотрена выше: индекс вектора в обучающей выборке - реализация случайной величины из заданного распределения вероятностей, например);

[math]D = InitialiseDistancesVector()[/math] - заполнение массива растояний нулями;

[math]d= CalculateDistanseBetweenInputVectorAndNeuronWeightsVector(x,n)[/math] - вычисление расстояния между входным вектором и вектора веса нейрона по выбранной метрике (например, евклидовом);

[math]PutCalculatedDistanceToDistancesVector(D, d)[/math] - добавление вычисленного расстояния между входным вектором и вектором веса текущего нейрона в массив расстояний;

[math]ne_c = FindNeuronWinner(D)[/math] - нахождение нерона победителя, индекс которого является индексом минимума в массиве расстояний;

[math]CorrectNeuronsWeightsVector(W)[/math] - корректировка весов нейронов по формуле: [math] \vec{w}^{(j)}(t+1) := \vec{w}^{(j)}(t) +\alpha(t)h_{ci}(t)[\vec{x}^{(i)}(t) - \vec{w}^{(j)}(t)][/math];

[math]DefineInputVectorToCluster()[/math] - определение входного вектора в соответсвующий кластер, концептуально ничем не отличается от нахождения нейрона-победителя, однако отвечает за формальный вывод результата.

1.6 Последовательная сложность алгоритма

Начнём рассмотрение сложности последовательной реализации алгоритма Кохонена «сверху – вниз» начиная со сложности максимально абстрактного набора функций и потом конкретизируя сложность каждой функции в рамках фундаментальных вычислительных операций (присваивание, суммирование и т.п.). Это позволяет пересчитать сложность алгоритма Кохонена при условии замены функции составляющих его основу и при реализации его на целевую платформу.

I АЛГОРИТМ ОБУЧЕНИЯ

1) Уровень набора функций

[math]Complexity(SOMLearning) = [/math]

[math]Complexity(SetAlgorithmParameters) +[/math]

[math]Complexity(CalculateDistancesBetweenNeuronsInEuclidianPlane) +[/math]

[math]Complexity(SetNeuronWeightsVector) +[/math]

[math]T \cdot Complexity(ChooseInputVector) +[/math]

[math]T \cdot Complexity(InitialiseDistancesVector) +[/math]

[math]T \cdot M \cdot Complexity(CalculateDistanseBetweenInputVectorAndNeuronWeightsVector) +[/math]

[math]T \cdot M \cdot Complexity(PutCalculatedDistanceToDistancesVector) +[/math]

[math]T \cdot Complexity(FindNeuronWinner) +[/math]

[math]T \cdot M \cdot Complexity(CorrectNeuronsWeightsVector)[/math]

2) Уровень реализации функций в рамках фундаментальных операций

Будем считать, что следующие операции выполняются за константное время ([math]O(1)[/math]):

[math]mov[/math] - присваивание

[math]sqrt[/math] - взятие квадратного корня из числа

[math]rand[/math] – генерация случайного числа

[math]add[/math] - сложение

[math]sub[/math] - вычитание

[math]mul[/math] - умножение

[math]comp[/math] - сравнение

[math]exp[/math] - экспоненцирование

[math]div[/math] - деление

Тогда:

[math]Complexity(SetAlgorithmParameters) = O(Complexity(mov)) = O(1)[/math], так как параметров всегда конечное число и мы делаем допущение, что это число меньше M и T

[math]Complexity(CalculateDistancesBetweenNeuronsInEuclidianPlane) = [/math] [math]O(M \cdot (M-1) \cdot (2 \cdot Complexity(sub) + 2 \cdot Complexity(mul) +[/math] [math] Complexity(add) + Complexity(sqrt))) = O(M^2)[/math]

[math]Complexity(SetNeuronWeightsVector) = O(M \cdot Complexity(mov)) \vee O(M \cdot Complexity(rand))) = O(M)[/math]

[math]Complexity(ChooseInputVector) = O(n \cdot Complexity(mov))= O(n)[/math]

[math]Complexity(InitialiseDistancesVector) = O(M \cdot n \cdot Complexity(mov)) = O(M \cdot n)[/math]

[math]Complexity(CalculatedDistanseBetweenInputVectorAndNeuronWeightsVector) = O(n \cdot Complexity(sub)) +[/math] [math]O(n \cdot Complexity(mul)) + O((n - 1) \cdot Complexity(add)) = O(n)[/math]

[math]Complexity(PutCalculatedDistanceToDistancesVector) = O(n \cdot Complexity(mov)) = O(n)[/math]

[math]Complexity(FindNeuronWinner) = O(M \cdot n \cdot Complexity(comp)) = O(Mn)[/math]

[math]Complexity(CorrectNeuronsWeightsVector) = O(nComplexity(add)) + O(nComplexity(mul)) + [/math] [math]O(Complexity(NeighborhoodFunction)) = O(n) + O(Complexity(NeighborhoodFunction)) = O(n) +[/math] [math] O(Complexity(exp) + Complexity(div)) = O(n)[/math]

3) Конечная сложность

[math]Complexity(SOMLearning) = O(1) + O(M^2) + O(M) + O(Tn) + O(TMn) + O(TMn) + O(TMn) + O(TMn) + O(TMn) =[/math]

[math] O(TMn) + O(M^2)[/math]

II АЛГОРИТМ РАБОТЫ

1) Уровень набора функций

[math]Complexity(SOMWorking) = [/math]

[math]T \cdot Complexity(ChooseInputVector) +[/math]

[math]T \cdot Complexity(InitialiseDistancesVector) +[/math]

[math]T \cdot K \cdot Complexity(CalculateDistanseBetweenInputVectorAndNeuronWeightsVector) +[/math]

[math]T \cdot K \cdot Complexity(PutCalculatedDistanceToDistancesVector) +[/math]

[math]T \cdot Complexity(FindNeuronWinner) +[/math]

[math]T \cdot Complexity(DefineInputVectorToCluster)[/math]

2) Уровень реализации функций в рамках фундаментальных операций

Эквивалентно п.2 в Алгоритме обучения (но в качестве M у нас K).

[math]Complexity(DefineInputVectorToCluster) = O(1)[/math]

3) Конечная сложность

[math]Complexity(SOMWorking) = O(Tn) + O(TKn) + O(TKn) + O(TKn) + O(TKn) + O(T) = O(TKn)[/math]

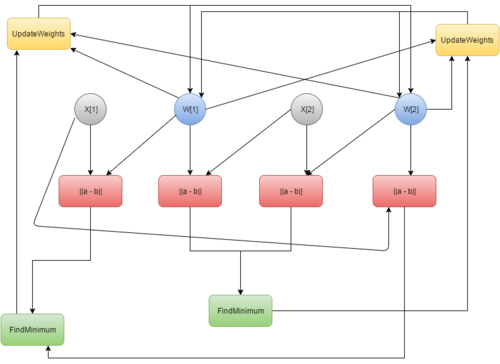
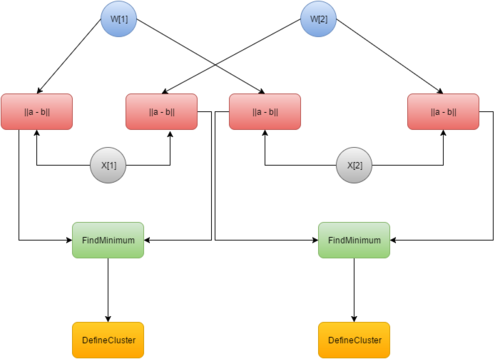
1.7 Информационный граф

Рис. 3а.Информационный граф алгоритма обучения

В качестве операторных узлов информационного графа были выбраны:

• ||a – b|| - взятие евклидовой метрики от двух операндов

• FindMinimum – нахождение минимума из входящих значений

• UpdateWeights – обновление весов (для каждого входящего вектора отдельный узел)

• DefineCluster – определение кластера на основе полученного значения от нахождения минимума

Это обусловлено тем, что с нашей точки зрения именно такой набор операций наиболее оптимально показывает структуру алгоритма, избавляя нас от излишней детализации.

Рис. 3б.Информационный граф алгоритма работы

1.8 Ресурс параллелизма алгоритма

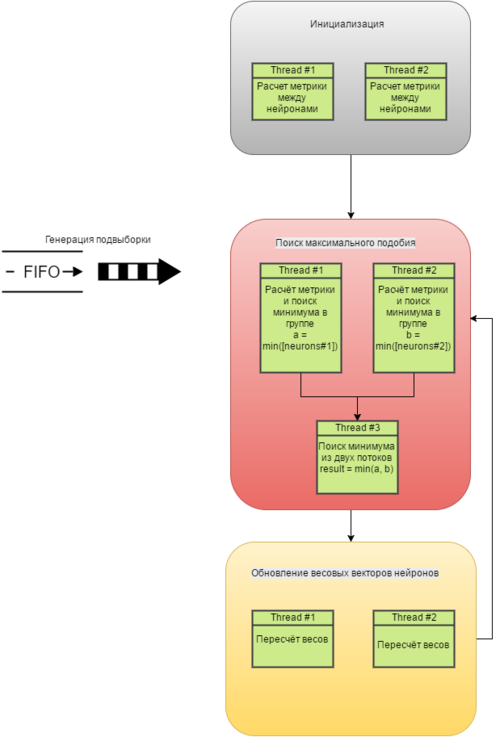
Для того чтобы оценить насколько эффективно Алгоритм Кохонена параллелизуется, рассмотрим его структуру в виде последовательности этапов исполнения. Вначале рассмотрим алгоритм обучения. У нас есть 4 фундаментальных этапа:

threadNumber = 2

1) Инициализация. На этом этапе мы определяем параметры алгоритма, рассчитываем расстояния между нейронами и определяем начальные веса нейронов. Здесь имеет смысл распараллелить подсчет метрики между нейронами. Таким образом асимптотическая сложность упадет с [math]O(M^2)[/math] до [math]O(M^2/threadNumber)[/math]

2) Генерация подвыборки. Здесь мы определяем в каком порядке будем обрабатывать вектора исходного входного пространства, какой вектор возьмём для следующей итерации. К сожалению, эта стадия не поддается распараллеливанию, так как каждая итерация алгоритма зависит от предыдущей;

3) Поиск максимального подобия. Находим наиболее подходящий (победивший) нейрон, используя критерий минимума Евклидова расстояния. Этот этап распараллеливается следующим образом. Вначале мы рассчитываем метрику между вектором весов каждого нейрона и входящим вектором исходного пространства, для этого мы разбиваем количество нейронов [math]M[/math] на [math]threadNumber[/math] потоков и подсчитываем метрику в каждой группе нейронов на поток параллельно. Затем мы пользуемся фактом, что минимум – дистрибутивная функция ([math]min([a, b, c, d] = min(min([a, b]), min([b, c]))[/math] см. Рис. 4) и рассчитываем её за [math]\log_{2} (threadNnumber)[/math] операций сравнения, что значительно меньше [math]M[/math] в исходном варианте;

4) Коррекция. Корректируем векторы синаптических всех нейронов. Также очевидным образом распараллеливаается на [math]threadNumber[/math] потоков, в каждым из которых последовательно для каждого нейрона в группе внутри потока обновляются веса.

Итак, общая сложность параллельной версии алгоритма обучения [math]O(Complexity(SOMParallel)) = O(M^2/threadNumber) + [/math] [math]O(TMn / threadNumber + \log_{2} (threadNumber)) + O(TMn/threadNumber)[/math] что меньше последовательной (при [math]threadNumber \approx M[/math]) [math]O(Complexity(SOMParallel)) = O(M^2) + O(TMn) + O(TMn)[/math].

Алгоритм работы карты эквивалентен первым 3 уровням алгоритма обучения только с другими константами ([math] M \leftarow K [/math]).

Вывод: Проведенный обзор показал, что только этап этап генерации подвыборки не поддается распараллеливанию. Это типичная проблема большинства алгоритмов машинного обучения, так как они итеративны (последовательно обучается по всей выборке). Однако в рамках остальных этапов алгоритм легко разбивается на потоки, что в теории улучшает производительность.

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

Авторами проекта была также практически написана собственная реализация (возможно, она будет доведена до конца и протестирована).

На данный момент удалось найти следующие последовательные реализации:

• KNNL:Реализация на C++
• kohonen Реалиазция на Python
• kohonen Реалиазция на R
• JKNNL: Реалиазция на Java.
• Matlab realization: Реалиазция на Matlab.

Также есть параллельные реализации:

• Somoclu: Реализация на Python, R, Julia, и Matlab, поддерживаются OpenMP, MPI и CUDA.