Участница:Tameeva.a/Метод Якоби вычисления собственных значений симметричной матрицы
| Метод Якоби вычисления собственных значений симметричной матрицы | |
| Последовательный алгоритм | |
| Последовательная сложность | O(n^3) |
| Объём входных данных | \frac{n (n + 1)}{2} |
| Объём выходных данных | n |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | O(n^2) |
| Ширина ярусно-параллельной формы | O(n) |
Основные авторы описания: А. Тамеева, А. Кухтинов.
Содержание
- 1 ЧАСТЬ. Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма[2]
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 ЧАСТЬ. Программная реализация алгоритма
- 3 Литература
1 ЧАСТЬ. Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Метод Якоби вычисления собственных значений симметричной матрицы — итерационный алгоритм, названный в честь предложившего его для конкретной матрицы 7 × 7 в 1846 году Карла Густава Якоба Якоби[1]. Исторически старейший метод для решения симметрической проблемы собственных значений получил широкое применение только в 1950-х годах с появлением компьютеров. Преимуществом метода является более точное вычисление малых собственных значений по сравнению с конкурирующими алгоритмами.
Суть алгоритма — приведение симметрической матрицы к диагональной с собственными значениями на диагонали путем вращения.
1.2 Математическое описание алгоритма[2]
Исходные данные: симметрическая матрица A=\{a_{ij}\}.
Вычисляемые данные: диагональная матрица \Lambda=\{\lambda_{ii}\}. Диагональные элементы \Lambda — собственные значения матрицы A, столбцы — приближенные собственные вектора матрицы A.
По заданной матрице A=A_0 строится последовательность ортогонально подобных матриц A_1, A_2,\ldots, A_m, сходящихся к \Lambda.
A_{i+1}={J_i}^TA_iJ_i, где J_i — ортогональная матрица, называемая вращением Якоби.
Матрица J_i выбирается так, чтобы обнулить элементы (j,k) и (k,j) матрицы A_{i+1}:
j k
\begin{align} J_i = R(j,k,\theta) = \begin{matrix} \\ \\ \\ j \\ \\ k \\ \\ \\ \\ \end{matrix} \begin{bmatrix} & 1 & & & & & & & & \\ & & 1 & & & & & & & \\ & & & \ddots & & & & & & \\ & & & & \cos(\theta) & & -\sin(\theta) & & & \\ & & & & & \ddots & & & & \\ & & & & \sin(\theta) & & \cos(\theta) & & & \\ & & & & & & & \ddots & & \\ & & & & & & & & 1 & \\ & & & & & & & & & 1 \\ \end{bmatrix} \end{align}
Для угла вращения \theta:
\begin{bmatrix}a^{(i+1)}_{jj} & a^{(i+1)}_{jk} \\ a^{(i+1)}_{kj} & a^{(i+1)}_{kk}\end{bmatrix}= \begin{bmatrix}\cos\theta & -\sin\theta \\ \sin\theta &\cos\theta\end{bmatrix}^{T} \begin{bmatrix}a^{(i)}_{jj} & a^{(i)}_{jk} \\ a^{(i)}_{kj} & a^{(i)}_{kk}\end{bmatrix} \begin{bmatrix}\cos\theta & -\sin\theta \\ \sin\theta &\cos\theta\end{bmatrix}= \begin{bmatrix}\lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix}, где \lambda_1 и \lambda_2 — собственные значения подматрицы \begin{bmatrix}a^{(i)}_{jj} & a^{(i)}_{jk} \\ a^{(i)}_{kj} & a^{(i)}_{kk}\end{bmatrix}.
Вычислим s = \sin \theta и c = \cos \theta, исходя из предыдущего матричного равенства:
\begin{bmatrix}\lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix}= \begin{bmatrix}a_{jj}c^2+a_{kk}s^2+2sca_{jk} & sc(a_{kk} - a_{jj}) + a_{jk}(c^2-s^2) \\ sc(a_{kk} - a_{jj}) + a_{jk}(c^2-s^2) & a_{jj}s^2+a_{kk}c^2 - 2sca_{jk} \end{bmatrix}.
Приравняем внедиагональный элемент нулю: \dfrac{a_{jj}-a_{kk}}{2a_{jk}}=\dfrac{c^2-s^2}{2sc}=\dfrac{\cos2\theta}{\sin2\theta}=\operatorname{ctg}2\theta\equiv\tau
Положим tg\theta=t=\dfrac{s}{c}. Тогда t^2+2t\tau-1=0.
Решая квадратное уравнение, получим: t=\dfrac{\operatorname{sign}\tau}{\left|\tau\right|+\sqrt{1+\tau^2}}, c=\dfrac{1}{\sqrt{1+t^2}}, s=t\cdot c.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма составляют вычисления элементов матрицы A в процессе применения матрицы поворота J :
1. Вычисления элементов a_{jl}^{(i+1)} = a_{lj}^{(i+1)} и a_{kl}^{(i+1)} = a_{lk}^{(i+1)} (каждое (n-2) раз):
\begin{align} a_{jl}^{(i+1)} = a_{lj}^{(i+1)} = c \, a_{jl}^{(i)} - s \, a_{kl}^{(i)}, l \ne j,k;\\ a_{kl}^{(i+1)} = a_{lk}^{(i+1)} = s \, a_{jl}^{(i)} + c \, a_{kl}^{(i)}, l \ne j,k. \end{align}
2. Вычисления элементов a_{jj}^{(i+1)} и a_{kk}^{(i+1)} :
\begin{align} a_{jj}^{(i+1)} &= c^2\, a_{jj}^{(i)} - 2\, s c \,a_{jk}^{(i)} + s^2\, a_{kk}^{(i)}; \\ a_{kk}^{(i+1)} &= s^2 \,a_{jj}^{(i)} + 2 s c\, a_{jk}^{(i)} + c^2 \, a_{kk}^{(i)}. \end{align}
1.4 Макроструктура алгоритма
Макроструктуру алгоритма можно описать следующим образом[3]:
repeat выбрать пару индексов j, k обратиться к процедуре JacobiRotation(A,j,k) пока А не станет достаточно близка к диагональной матрице
1.5 Схема реализации последовательного алгоритма
В классическом алгоритме Якоби для обнуления на текущей итерации выбирался наибольший элемент a_{jk}. Поиск наибольшего элемента слишком замедляет процесс вычислений (нужно провести поиск среди \dfrac{n^2-n}{2} элементов, прежде чем выполнить вращение стоимостью в O(n) флопов), поэтому для практических вычислений выбор параметров j и k производится путем построчного циклического обхода внедиагональных элементов матрицы A.
Таким образом, алгоритм можно описать так[4]:
repeat
for j=1 to n-1
for k=j+1 to n
выполнить процедуру JacobiRotation(A, j, k)
end for
end for
пока A не достаточно близка к диагональной матрице
Процедура JacobiRotation(A, j, k):
if [math]|a_{jk}|[/math] не слишком мал [math]\begin{align} \tau &= \frac{a_{jj}-a_{kk}}{2\,a_{jk}} \\ t &= \frac{sign(\tau)}{|\tau|+\sqrt{1+\tau^2}} \\ c &= \frac{1}{\sqrt{1+t^2}} \\ s &= c\cdot t \\ A &= J_i^T\cdot A\cdot J_i, \qquad J_i = R(j,k,\theta),\ c = \cos \theta,\ s = \sin \theta \end{align} [/math] end if
1.6 Последовательная сложность алгоритма
Для одной итерации вычислений собственных значений матрицы порядка n методом Якоби требуется:
Для вычислительного ядра:
- 4\,n+6 умножений,
- 2n сложений.
Для остальной части алгоритма:
- 4 умножений,
- 3 делений,
- 4 сложений (вычитаний),
- 2 операций извлечения квадратного корня.
Умножения и сложения (вычитания) составляют основную часть алгоритма.
Так как выбор индексов j и k осуществляется путем перебора внедиагональных элементов матрицы, для полного прохода потребуется \frac{n(n-1)}{2} итераций.
Таким образом, при классификации по последовательной сложности метод Якоби вычисления собственных значений симметричной матрицы относится к алгоритмам с кубической сложностью.
1.7 Информационный граф
Опишем граф алгоритма аналитически и в виде рисунка.
Граф алгоритма состоит из четырёх групп вершин:
1. Off>eps — сравнение матрицы с диагональной: вычисление нормы наддиагональных элементов of\!f(A)=\sqrt{\sum\limits_{1 \le j \lt k \le n} a_{jk}^2} и сравнение с \epsilon.
Аргументы функции:
- a_{jk}
- Первая итерация — элементы входных данных: наддиагональные элементы матрицы A;
- Последующие — результаты вычислений вершины четвертой группы (a^{i+1}_{jl},a^{i+1}_{kl},l\ne j,k);
- \epsilon — элемент входных данных.
Результат выполнения функции является промежуточным данным алгоритма.
2. Calculate c,s — вычисление c, s согласно формулам в схеме реализации последовательного алгоритма.
Аргументы функции:
- a^{(i+1)}_{jj}, a^{(i+1)}_{kk}:
- Первая итерация — элементы входных данных: диагональные элементы матрицы A;
- Последующие — результаты вычислений вершины третьей группы.
- a^{(i+1)}_{jk}
- Первая итерация — элементы входных данных a_{jk}
- Последующие — результаты вычислений вершины четвертой группы.
Результаты выполнения функции являются промежуточными данными алгоритма.
3. A_{jj}, A_{kk} — вычисление a^{(i+1)}_{jj}, a^{(i+1)}_{kk} согласно формулам в разделе Вычислительное ядро алгоритма.
Аргументы функции:
- c, s — результаты вычислений вершины второй группы.
- a^{(i)}_{jj}, a^{(i)}_{kk}:
- Первая итерация — элементы входных данных a_{jj}, a_{kk};
- Последующие — результаты вычислений вершины третьей группы.
- a^{(i)}_{jk}:
- Первая итерация — элементы входных данных a_{jk};
- Последующие — результаты вычислений вершины четвертой группы.
Результат выполнения функции является выходным данным алгоритма.
4. A_{jl}, A_{kl} — вычисление a^{(i+1)}_{jl},a^{(i+1)}_{kl},l\ne j,k согласно формулам в разделе Вычислительное ядро алгоритма.
Аргументы функции:
- c, s — результаты вычислений вершины второй группы.
- a^{(i)}_{jl}, a^{(i)}_{kl}:
- Первая итерация — элементы входных данных a_{jl},l\ne j,k;
- Последующие — результаты вычислений вершины четвертой группы.
Результат выполнения функции является промежуточным данным алгоритма. (Считается, что алгоритм вычисляет только собственные значения. При вычислении собственных векторов эти данные также были бы выходными)
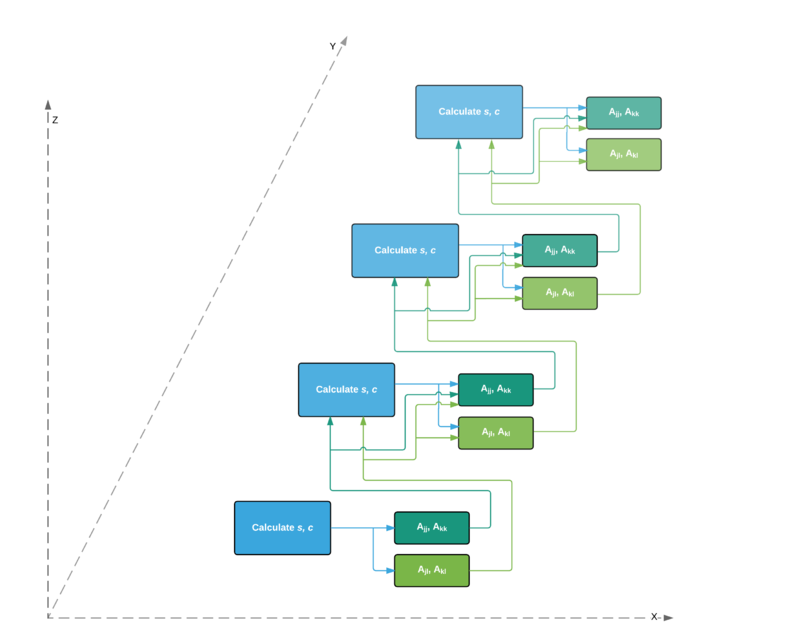
Описанный граф для четырех итераций представлен на рисунке. К графу добавлены вершины, соответствующие входным (желтый цвет) и выходным (фиолетовый цвет) данным. Дублирующие друг друга дуги даны как одна.
1.8 Ресурс параллелизма алгоритма
Для выполнения каждой итерации требуется последовательно выполнить следующие ярусы (для матрицы порядка n):
- Вычислить норму матрицы и сравнить с \epsilon (параллельное вычисление \frac{n(n-1)}{2} умножений, далее последовательно \frac{n(n-1)}{2}-1 сложений, 1 операция взятия квадратного корня, 1 операция сравнения )
- Вычислить \tau, t, c, s (последовательно всего 4 умножений, 3 делений, 4 сложений (вычитаний), 2 операции извлечения квадратного корня, 1 операция сравнения, 1 операция взятия модуля)
- Поворот матрицы A с параллельным выполнением 2(n-2) операций вычисления элементов матрицы a_{jl}^{(i+1)} = a_{lj}^{(i+1)} и a_{kl}^{(i+1)} = a_{lk}^{(i+1)}, m \ne j,k, а также 2 операций вычисления элементов a_{jj}^{(i+1)} и a_{kk}^{(i+1)} .
Суммарное количество итераций зависит от входных данных и заданного значения погрешности \epsilon. Один цикл (полный проход по внедиагональным элементам) осуществляется за N = \frac{n(n-1)}{2} итераций.
Таким образом, при классификации по высоте ЯПФ метод Якоби относится к алгоритмам со сложностью O(n^2) , а при классификации по ширине ЯПФ — к алгоритмам со сложностью O(n).
1.9 Входные и выходные данные алгоритма
Входные данные:
1. Плотная матрица A=\{a_{ij}\}, A\in\R^{n\times n}. Дополнительные ограничения:
- A — симметрическая матрица, т. е. a_{ij}= a_{ji}, i, j = 1, \ldots, n.
2. Число двойной точности \epsilon, определяющее допустимый порядок малости внедиагональных элементов.
Объём входных данных:
1. \frac{n (n + 1)}{2} (в силу симметричности достаточно хранить только диагональ и над- или поддиагональные элементы). В разных реализациях эта экономия хранения может быть выполнена разным образом.
Выходные данные: вектор собственных значений \lambda_{i} длины n.
Объём выходных данных: n
1.10 Свойства алгоритма
Из существующих алгоритмов вычисления собственных значений симметричной матрицы метод Якоби является самым медленным (в среднем для сходимости метода Якоби требуется от 5 до 10 циклов, что хуже, чем у конкурирующих алгоритмов[5]). Его преимущество заключается в том, что он не предполагает первоначального приведения матрицы к трехдиагональной форме. Также метод до сих пор используется на практике для вычисления малых собственных чисел и отвечающих им собственных векторов, так как он делает это с гораздо большей точностью, чем другие методы[6].
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов для метода Якоби является линейным, вычислительная мощность алгоритма также линейна.
Метод Якоби не детерминирован, так как является итерационным алгоритмом с выходом по точности: число итераций зависит от входных данных и порогового значения.
Дуги информационного графа, исходящие из вершин, соответствующих вычислениям значений c и s, образуют пучки рассылок линейной мощности.
2 ЧАСТЬ. Программная реализация алгоритма
2.1 Масштабируемость алгоритма и его реализации
2.2 Существующие реализации алгоритма
Библиотека JACOBI_EIGENVALUE содержит последовательную реализацию алгоритма.
Существует также параллельная реализация метода на платформе CUDA.
3 Литература
- ↑ Jacobi, C.G.J. (1846). «Über ein leichtes Verfahren, die in der Theorie der Säkularstörungen vorkommenden Gleichungen numerisch aufzulösen» (German). Crelle's Journal 30: 51–94.
- ↑ Дж. Деммель «Вычислительная линейная алгебра» (стр. 244-245)
- ↑ Дж. Деммель «Вычислительная линейная алгебра» (стр. 246, алгоритм 5.6)
- ↑ Дж. Деммель «Вычислительная линейная алгебра» (стр. 247, алгоритм 5.8)
- ↑ Дж. Деммель «Вычислительная линейная алгебра» (стр. 248)
- ↑ Дж. Деммель «Вычислительная линейная алгебра» (стр. 244)