Участник:Анюшева Ирина/Итерационный метод решения системы линейных алгебраических уравнений GMRES (обобщенный метод минимальных невязок)

GMRES (обобщенный метод минимальных невязок)
Последовательный алгоритм
Последовательная сложность	$O(m^2n^2)$
Объём входных данных	$n^2+2n$
Объём выходных данных	$n$
Параллельный алгоритм
Высота ярусно-параллельной формы	1
Ширина ярусно-параллельной формы	1

Основные авторы описания: Анюшева Ирина (614 группа, разделы: 1.1-1.2, 1.7-1.8, 2.7, 3), Исхаков Эльдар (614 группа, разделы 1.3-1.6, 1.9-1.10)

1 ЧАСТЬ. Свойства и структура алгоритма

1.1 Общее описание алгоритма

Обобщенный метод минимальных невязок (GMRES) для решения системы линейных алгебраических уравнений аппроксимирует решение с помощью вектора в подпространстве Крылова с минимальным остатком. Метод GMRES разработан Ю.Саадом и Мартин Х. Шульцом в 1986 году. Метод по праву считается одним из самых эффективных численных методов решения несимметричных систем. Он гарантирует неувеличение нормы невязки в ходе итерационного процесса, который основан на построении базиса в соответствующей системе подпространстве Крылова $K_j(A, r_0)$. Затем решение уточняется некоторой добавкой, представленной в виде разложения по этому базису.

Метод обобщенных минимальных невязок популярен из-за наличия ряда преимуществ: он ошибкоустойчив, допускает эффективное распараллеливание, не требует нахождения параметра релаксации, обладает суперлинейной скоростью сходимости. Однако в чистом виде для больших систем метод не используется из-за чрезвычайно больших затрат памяти. Зато широкое распространение получила перезапускаемая версия метода, подоразумевающая перезапуск метода каждые m итераций. Уменьшение размерности пространства может привести к стагнации метода – процессу, при котором с каждой следующей итерацией норма невязки уменьшается незначительно, либо не уменьшается вовсе.

1.2 Математическое описание алгоритма

Исходные данные: система линейных алгебраических уравнений $Ax=b$, где:

$A=(a_{ij})$ $-$ вещественная матрица размера $n \times n$;

$b$ и $x$ вектора из $n$ элементов;

$x^*$ $-$ точное решение системы.

Вычисляемые данные: $x^{(s)} -$приближенное решение системы.

1.2.1 Ортогонализация Арнольди

Для построения базиса $V$ в подпространстве Крылова в методе GMRES применяется ортогонализация Арнольди.

Формулы метода:

$\begin{align} (h_{i+1,i}v_{i+1}) & = Av_i - \sum_{j = 1}^{i} h_{j,i}v_j, \\ v_1 &= \frac{r_0}{\parallel r_0 \parallel}, \end{align}$

В матрично-векторных обозначениях соотношение может быть записано как

$\begin{align} AV_i &= V_i H_i + h_{i+1,i}v_{i+1} e_i^T &=V_{i+1}\overline{H}_i, \end{align}$

$\begin{align} V_i &= [v_1|v_2|...|v_i], \overline{H}_i - \end{align}$ верхняя матрица Хессенберга размерности $(i+1)\times i$

1.2.2 Минимизация невязки

Невязку уравнения можно определить как $J(y) = \parallel b- A x\parallel = \parallel b- (Ax_0+V_m y)\parallel =\parallel \beta e_1 - \overline{H}_m y \parallel$, где $y -$ вектор размерности $m$.

Вектор $x_m$ может быть получен как $x_m = x_0 + V_m y_m$, вектор $y_m$ может найден как решение линейной задачи наименьших квадратов размера $(m+1)\times m$, где $m\lt \lt n$.

Для решения задачи минимизации приведем матрицу $\overline{H}_m$ к верхнему треугольному виду с помощью вращений Гивенса. На шаге $i$ матрица вращения $\Omega_i$ имеет размеры $(m+1)\times (m+1)$ и имеет следующий вид:

$\Omega_i= \begin{pmatrix} 1 & &&&&&& \\ &\ddots &&&&&&\\ &&1&&&&& \\ &&&c_i&s_i &&& \\ &&&-s_i& c_i &&&\\ &&&&&1&&& \\ &&&&&&\ddots&\\ &&&&&&&1 \\ \end{pmatrix}$

1.3 Вычислительное ядро алгоритма

В алгоритме GMRES присутствуют два ресурсоемких с точки зрения вычислительных мощностей этапа:

• умножение исходной матрицы на вектор при вычислении невязок;

• вычисление скалярных произведений векторов при построении ортонормированного базиса подпространства Крылова.

1.4 Макроструктура алгоритма

Наиболее ресурсоемкие операции при выполнении алгоритма:

• Вычисление нормы невязки для задачи "начальных" условий;

• Вычисление элементов Хессенберговой матрицы - матрично-векторные умножения и скалярные произведения векторов;

• Вычисление произведений разреженных матриц при минимизации невязки.

1.5 Схема реализации последовательного алгоритма

1.5.1 Шаги алгоритма

1. Выбрать произвольное $x_0$; вычислить $r_0=b-Ax_0$ и $v_1=\frac{r_0}{\parallel r_0 \parallel}$

2. Задать матрицу $\overline{H}_m$ размерности $(m+1)\times m$ и всем ее элементам присвоить нулевые значения

3. Для $j=1,\dots,m$ выполнять:

• для $i=1,\dots,j$ выполнять: $h_{i,j}=(Av_j,v_i)$
• $\omega_j=Av_j-\sum_{i=1}^j h_{i,j}v_i$
• $h_{j+1,j}={\parallel \omega_j \parallel}$
• $v_{j+1}=\frac{\omega_j}{h_{j+1,j}}$

4. Вычислить $y_m=\arg\min_{y} \parallel \beta e_1 - \overline{H}_my \parallel,\ y \in \mathbb{R}^m$ и $x_m=x_0+V_my_m$

5. Вычислить $r_m=b-Ax_m$. Если достигнутая точность удовлетворительна, остановиться.

Иначе принять $x_0=x_m$ и $v_1=\frac{r_m}{\parallel r_m \parallel}$ и вернуться к пункту 2.

1.5.2 Решение задачи минимизации невязки

Для нахождения $y_m=\arg\min_{y} \parallel \beta e_1 - \overline{H}_my \parallel$ необходимо выполнить следующие шаги:

1. Найти $m$ матриц вращений Гивенса $\Omega_i(c_i,s_i),\ i=1,\dots,m$ размера $(m+1)\times(m+1)$, где $s_i=\frac{h_{i+1,i}}{\sqrt{h_{i,i}^2+h_{i+1,i}^2}}$, $c_i=\frac{h_{i,i}}{\sqrt{h_{i,i}^2+h_{i+1,i}^2}}$

2. Вычислить $\overline{H}_m^{(m)}=\Omega_1\dots\Omega_m\overline{H}_m$ и $\overline{g}_m=\Omega_1\dots\Omega_m\beta e_1$, удалить последнюю строку и последний элемент соответственно и решить СЛАУ с полученной верхнетреугольной матрицей и правой частью. Полученное решение $y_m$ минимизирует исходный функционал.

1.6 Последовательная сложность алгоритма

Для выполнения одной итерации алгоритма необходимо произвести:

• $3m+1$ делений;

• $2m+1$ вычислений квадратного корня;

• $n^2+\frac{3m+5}{2}n$ умножений;

• $O(\frac{m^2n^2}{2})$ сложений (вычитаний).

1.7 Информационный граф

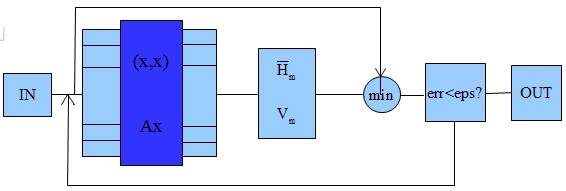
Метод состоит из двух блоков: ортогонализация и минимизация невязки. При ортогонализации основными операциями являются умножение матрицы на вектор и скалярное умножение векторов, для которых возможен параллелизм, что показано в блоке на темно-синем фоне. В блоке $min$ решается задача минимизации невязки, которая, строго говоря, является отдельной самостоятельной задачей.

Рис.1. Информационная структура алгоритма GMRES

1.8 Ресурс параллелизма алгоритма

Для нахождения матрично-векторных произведений при вычислении невязок матрица СЛАУ должна быть подвергнута декомпозиции на строчные блоки, размеры которых определяются требованиями равномерности загрузки. Соответствующим образом подвергается декомпозиции и вектор правой части. Для наиболее эффективного вычисления скалярных произведений и линейных комбинаций векторов базиса каждый из векторов $v_j$ должен быть разбит на блоки равного размера по числу процессов; каждый из процессов при этом хранит соответствующие блоки всех векторов. Обработка вектора решения дублируется на всех процессах.

1.9 Входные и выходные данные алгоритма

Входные данные:

• матрица $A$ размера $n\times n$;
• вектор-столбец $b$ размера $n$;
• вектор-столбец $x_0$ размера $n$ - начальное приближение;
• натуральное число $m\lt \lt n$, определяющее размерность подпространства Крылова.

Выходные данные:

• вектор-столбец $x$ размера $n$ - решение системы.

1.10 Свойства алгоритма

• Вычислительная мощность: весьма маленькая и равна $m^2$, так как $m\lt \lt n$.

• Устойчивость: GMRES в этом плане является очень хорошим методом. Теоретически можно получить точное решение не более чем за $n$ итераций. Однако, очень приемлемые результаты получаются и за $m\lt \lt n$ итераций. Однако, есть примеры, в которых видно, что первые $m-1$ итераций дают невязку, равную некой константе, а на итерации под номером $m$ получаем точное решение.

2 ЧАСТЬ. Программная реализация алгоритма

2.7 Существующие реализации алгоритма

• Реализация алгоритма в библиотеках LASpack, IML++, SciPy
• Библиотека для MATLAB: http://www.mathworks.com/help/matlab/ref/gmres.html

3 ЧАСТЬ. Литература

1. Y. Saad, M.H. Schultz. GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Statist. Comput., 7 (1986), pp. 856–869

2. Е.Е. Тыртышников. Методы численного анализа. – Москва: Академия, 2007

3. М.Ю. Баландин, Э.П. Шурина. Некоторые оценки эффективности параллельных алгоритмов решения СЛАУ на подпространствах Крылова. - Вычислительные технологии, том 3, №1, 1998