Участник:Karibov/Алгоритм кластеризации с использованием представлений

Алгоритм кластеризации с использованием представлений
Последовательный алгоритм
Последовательная сложность	[math][/math]
Объём входных данных	[math][/math]
Объём выходных данных	[math][/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math][/math]
Ширина ярусно-параллельной формы	[math][/math]

Основные авторы описания: Карибов Евгений, Курашов Александр

1 ЧАСТЬ. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Выполняет иерархическую кластеризацию с использованием набора определяющих точек для определения объекта в кластер.

Назначение: кластеризация очень больших наборов числовых данных.

Ограничения: эффективен для данных низкой размерности, работает только на числовых данных.

Описание алгоритма [1]:

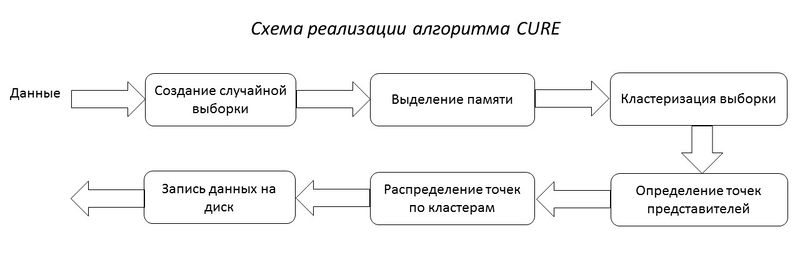
Шаг 1: Построение дерева кластеров, состоящего из каждой строки входного набора данных.

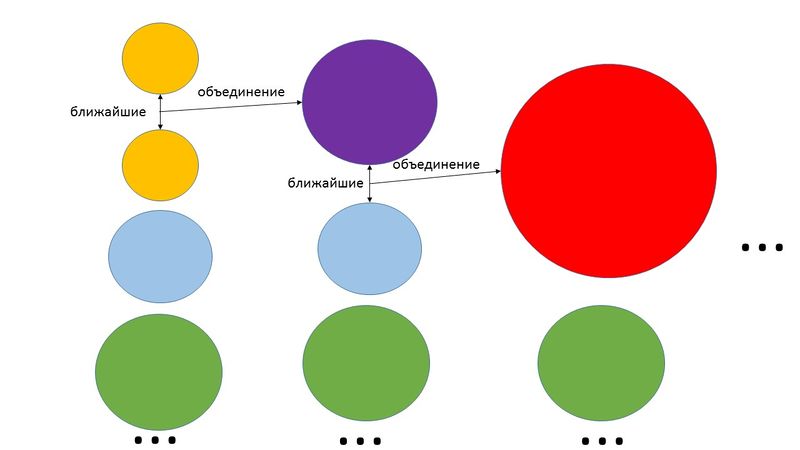
Шаг 2: Формирование «кучи» в оперативной памяти, расчет расстояния до ближайшего кластера (строки данных) для каждого кластера. При формировании кучи кластеры сортируются по возрастанию дистанции от кластера до ближайшего кластера. Расстояние между кластерами определяется по двум ближайшим элементам из соседних кластеров. Для определения расстояния между кластерами используются «манхеттенская», «евклидова» метрики или похожие на них функции.

Шаг 3: Слияние ближних кластеров в один кластер. Новый кластер получает все точки входящих в него входных данных. Расчет расстояния до остальных кластеров для новообразованного кластера. Для расчета расстояния кластеры делятся на две группы: первая группа – кластеры, у которых ближайшими кластерами считаются кластеры, входящие в новообразованный кластер, остальные кластеры – вторая группа. И при этом для кластеров из первой группы, если расстояние до новообразованного кластера меньше чем до предыдущего ближайшего кластера, то ближайший кластер меняется на новообразованный кластер. В противном случае ищется новый ближайший кластер, но при этом не берутся кластеры, расстояния до которых больше, чем до новообразованного кластера. Для кластеров второй группы выполняется следующее: если расстояние до новообразованного кластера ближе, чем предыдущий ближайший кластер, то ближайший кластер меняется. В противном случае ничего не происходит.

Шаг 4: Переход на шаг 3, если не получено требуемое количество кластеров.

1.2 Математическое описание алгоритма

Исходные данные: множество данных [math]\{p_i\}[/math], [math]k[/math] - число кластеров, на которое необходимо разбить множество, число точек представителей [math]c[/math], параметр [math]\alpha[/math] для сжатия точек представления к центру кластера, [math]m[/math] число точек для кластеризации, [math]n[/math] - размерность множества, параметр [math]\gamma[/math] задаёт какая часть от [math]m[/math] точек будет использована при случайной инициализации.

Вычисляемые данные: множества [math]C_i, i = 1..k[/math]

Формулы метода:

Для каждого [math]C_i[/math] вычисляем центроид: [math]\mu _i = \frac{1}{n_i} \sum^{}_{j \in C_i} {j}[/math], [math]n_i [/math] - количество точек в кластере [math]C_i[/math]

Для вычисления расстояния между кластерами для поиска подходящим для объединения кластеров могут быть использованы следующие формулы:

[math]d_{mean}(C_i, C_j) = \left \|\mu _i - \mu _j\right \|[/math];

[math]d_{ave}(C_i, C_j) = \frac{1}{n_in_j} {\sum^{}_{p\in C_i} {\sum^{}_{p'\in C_j} {\left \|p - p'\right \|}}}[/math];

[math]d_{max}(C_i, C_j) = \max_{p'\in C_j, p'\in C_j}\left \|p - p'\right \|[/math];

[math]d_{min}(C_i, C_j) = \min_{p'\in C_j, p'\in C_j}\left \|p - p'\right \|[/math].

Объединяем ближайшие кластеры.

Затем для каждого кластера определяются [math]c[/math] точек представителей максимально удалённых друг от друга.

Затем каждую точку представителя выполняется сдвигают к центроиде соответствующего кластера в [math]\alpha[/math] раз.

Затем происходит присвоение неиспользованных точек к кластерам.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма представляет собой итерационное построение [math]k[/math] кластеров, вычисление их центроидов и назначение точек представителей.

1.4 Макроструктура алгоритма

Основную часть метода составляют разбиение случайной выборки строк на [math]k[/math] кластеров и нахождение точек-представителей для каждого кластера.

1.5 Схема реализации последовательного алгоритма

Рисунок 1. Схема реализации [2]

1.6 Последовательная сложность алгоритма

В худшем случае иерархический алгоритм кластеризации имеет сложность [math]O(n^2 log(n))[/math]. Для пространств небольших размерностей достигается сложность [math]O(n^2)[/math].

1.7 Информационный граф

В начале работы алгоритма все объекты являются отдельными кластерами. На первом шаге наиболее похожие объекты объединяются в кластер. На последующих шагах объединение продолжается до тех пор, пока число кластеров не будет равно [math]k[/math].

Рисунок 2. Информационный граф

1.8 Ресурс параллелизма алгоритма

Каждый шаг алгоритма выполняется независимо от других кластеров и их представителей. Это дает предпосылки к возможности хорошего распараллеливания метода кластеризации на каждом этапе алгоритма.

1.9 Входные и выходные данные алгоритма

Входные данные: множество данных [math]\{p_i\}[/math], [math]k[/math] - число кластеров, на которое необходимо разбить множество, число точек представителей [math]c[/math], параметр [math]\alpha[/math] для сжатия точек представления к центру кластера, [math]m[/math] число точек для кластеризации, [math]n[/math] - размерность множества, параметр [math]\gamma[/math] задаёт какая часть от [math]m[/math] точек будет использована при случайной инициализации.

Выходные данные: множества [math]C_i, i = 1..k[/math]

1.10 Свойства алгоритма

Достоинства: выполняет кластеризацию на высоком уровне даже при наличии выбросов, выделяет кластеры сложной формы и различных размеров, обладает линейно зависимыми требованиями к месту хранения данных и временную сложность для данных высокой размерности.

Недостатки: есть необходимость в задании пороговых значений и количества кластеров [1].

2 ЧАСТЬ. Программная реализация алгоритма

2.7 Существующие реализации алгоритма

Последовательная реализация CURE-алгоритма для кластеризации для Python/C++ представлена в пакете: pyclustering.

Также существует параллельная реализация алгоритма, описанная в сборнике [3].

3 Литература

[1] Нейский И.М. Классификация и сравнение методов кластеризации http://it-claim.ru/Persons/Neyskiy/Article2_Neiskiy.pdf.

[2] Guha, Sudipto; Rastogi, Rajeev; Shim, Kyuseok (2001). "CURE: An Efficient Clustering Algorithm for Large Databases" (PDF). Information Systems. 26 (1): 35–58. doi:10.1016/S0306-4379(01)00008-4.

[3] Panagiotis E. Hadjidoukas, Laurent Amsaleg. OpenMP Shared Memory Parallel Programming. Volume 4315 of the series Lecture Notes in Computer Science pp 289-299 Parallelization of a Hierarchical Data Clustering Algorithm Using OpenMP.

[4] Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ-Петербург, 2002.