Участник:Ян-Мартин Тамм/Строгий алгоритм С средних

Строгий алгоритм С средних (K-means, Hard C-Means)
Последовательный алгоритм
Последовательная сложность	[math]O(nkdi)[/math]
Объём входных данных	[math]nd+1[/math]
Объём выходных данных	[math]nk[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(log_2(k)log_2(d)i)[/math]
Ширина ярусно-параллельной формы	[math]O(nkd)[/math]

Автор: Ян-Мартин Тамм

1 Описание алгоритма

1.1 Общее описание алгоритма

Строгий алгоритм C средних, более известный как K-средних, решает задачу разделения векторов в многомерном пространстве на заданное количество кластеров. При этом каждый вектор принадлежит только одному кластеру, поэтому алгоритм называется строгим, в то время как нечеткий алгоритм C средних (Fuzzy C-means, Soft K-means) определяет степень принадлежности вектора каждому из кластеров.
Данная задача является NP-трудной, тем не менее описываемый алгоритм сходится к локальному оптимуму. Глобальный оптимум не гарантируется и зависит от первоначального распределения центров кластеров и их количества.
Общая идея алгоритма такова: фиксируем число кластеров [math]k[/math], произвольным образом выбираем центры кластеров, после чего повторяем следующие два действия, пока не будет выполнено условие остановки:

1. Распределяем каждый вектор в ближайший кластер
2. Пересчитываем значения центров как среднее значение координат векторов в каждом кластере

Минимизируется сумма расстояний векторов от центров их кластеров. Остановка производится если либо значение данной функции становится ниже некоторого порога, либо мало изменяется по сравнению с предыдущей итерацией.

1.2 Математическое описание алгоритма

Дано множество d-мерных векторов  [math]U=\{u_1, u_2, ..., u_n\}[/math] и число кластеров [math]k \in \mathbb{N}[/math]. Требуется разбить множество [math]U[/math] на [math]k[/math] непересекающихся непустых кластеров [math]C_1, C_2, ..., C_k[/math] таких, что [math]{\bigcup \limits _{i = 1}^k C_i} = U [/math].
Для этого минимизируется функция [math] J = \sum\limits_{i=1}^k J_i = \sum\limits_{i=1}^k \sum\limits_{ u \in C_i} \|u-c_i \|^2 [/math], где [math]c_i[/math]— центр масс векторов кластера [math]C_i[/math].
Произвольным образом инициализируем центры кластеров [math]c_1, c_2, ..., c_k[/math], после чего начинается основная часть алгоритма.

• Каждый вектор [math]u_l[/math] определяем в ближайший к нему кластер [math]C_i[/math], то есть такой, что [math] \|u_l-c_i\|^2 \leqslant \|u_l-c_j\|^2 \;\; \forall i \neq j; \;\; (i,j=1,2,\ldots,k, \; l = 1,2,\ldots,n) [/math].
Хранить информацию о принадлежности векторов кластерам будем в матрице [math]M[/math] следующего вида:

[math] m_{ij} = \begin{cases} 1, & u_j \in C_i \\ 0, & \text{otherwise} \end{cases} [/math]

• Считаем значение функции [math]J[/math] и прекращаем работу алгоритма, если это значение меньше заданного порога [math]\varepsilon[/math], либо значение мало изменилось после текущей итерации.
• Обновляем значения центров кластеров

  [math] c_i = \frac{1}{|C_i|} \sum\limits_{u \in C_i} u \;\; (i=1,2,\ldots,k) [/math]

• Возвращаемся к распределению векторов по кластерам.

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма является весь алгоритм, а именно два основных его шага:

• Распределение векторов по кластерам
• Пересчёт центров кластеров

1.4 Макроструктура алгоритма

Как уже говорилось раньше, первоначальное распределение векторов по кластерам может быть произвольным, например, можно случайным образом выбрать [math]k[/math] векторов из множества всех векторов [math]U[/math].
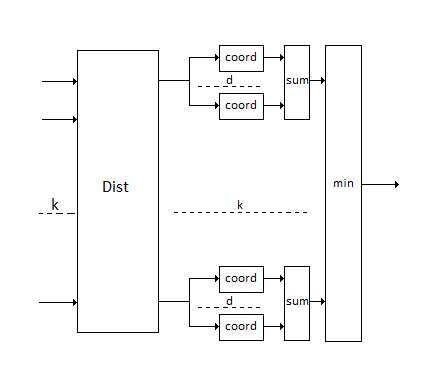
Далее начинается цикл, его первая операция — распределение векторов по кластерам. В ней для каждого вектора считается расстояние от него, до каждого кластера [math]\rho = \big \| u - c \big \|^2=\sum_{i=1}^d (u_i-c_i)^2[/math], после чего из них выбирается наименьшее и заносится в матрицу.
Подсчёт функции [math]J[/math] можно проводить одновременно с первым шагом, так как в ней суммируются те же самые расстояния.
Пересчёт центров кластеров — сумма всех векторов кластера, делённая на количество объектов в кластере. [math] c = \frac{1}{|C|} \sum\limits_{u \in C} u [/math]

1.5 Схема реализации последовательного алгоритма

def kmeans(points, k, cutoff):
    
    # Pick out k random points to use as our initial centroids
    initial = random.sample(points, k)
    
    # Create k clusters using those centroids
    clusters = [Cluster([p]) for p in initial]
    
    # Loop through the dataset until the clusters stabilize
    while True:
        # Create a list of lists to hold the points in each cluster
        lists = [ [] for c in clusters]

        # For every point in the dataset ...
        for p in points:
            # Get the distance between that point and the centroid of the first cluster.
            smallest_distance = getDistance(p, clusters[0].centroid)
        
            # Set the cluster this point belongs to
            clusterIndex = 0
        
            # For the remainder of the clusters ...
            for i in range(clusterCount - 1):
                # calculate the distance of that point to each other cluster's centroid
                distance = getDistance(p, clusters[i+1].centroid)
                # If it's closer to that cluster's centroid update what we
                # think the smallest distance is, and set the point to belong to that cluster
                if distance < smallest_distance:
                    smallest_distance = distance
                    clusterIndex = i+1
            lists[clusterIndex].append(p)
        
        # Set our total_shift to zero for this iteration
        total_shift = 0.0
        
        # As many times as there are clusters ...
        for i in range(k):
            # Calculate how far the centroid moved in this iteration
            shift = clusters[i].update(lists[i])
            # Keep track of the total moves from all cluster centroid updates
            total_shift += shift
        
        # If the centroids have stopped moving much, we're done!
        if total_shift < cutoff:
            break
    return clusters

1.6 Последовательная сложность алгоритма

Распределение по кластерам — для каждого из [math]n[/math] векторов и каждого из [math]k[/math] кластеров посчитать расстояние, сложив [math]d[/math] раз значения, на вычисление каждого из которых нужно 2 операции — [math]O(nkd)[/math]. Пересчёт центров — [math]n[/math] раз сложить и [math]k[/math] раз поделить —  [math]O(n+k)[/math]. На завершение алгоритма понадобится [math]i[/math] итераций. Итого сложность [math]O(nkdi)[/math].

1.7 Информационный граф

На рисунке ниже приведён информационный граф алгоритма.

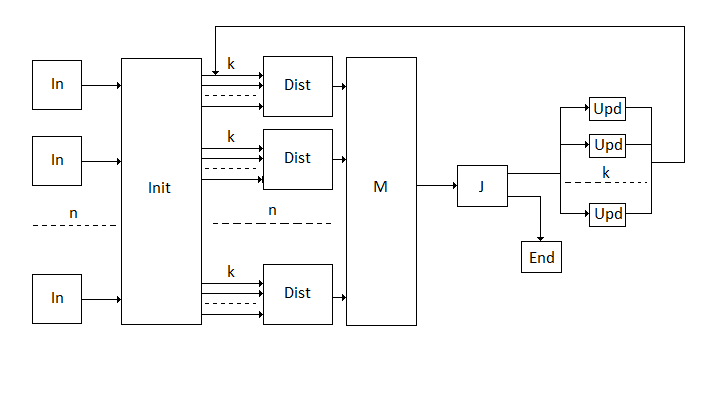
Блок, определяющий ближайший кластер, подробнее.

1.8 Ресурс параллелизма алгоритма

Самой трудоёмкой операцией является распределение по кластерам. Так, для рассчёта расстояний, можно провести суммирование [math]d[/math] элементов за [math]log_2(d)[/math] операций. Расстояние от данного вектора до всех кластеров можно найти за одну операцию, после чего нужно найти наименьшее значение из [math]k[/math] элементов за [math]log_2(k)[/math] операций. И всё это нужно сделать для [math]n[/math] векторов, что можно сделать параллельно за одну операцию. Для сходимости всё так же потребуется [math]i[/math] итераций, общая сложность получается [math]O(log_2(k)log_2(d)i)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные:

• [math]U=\{u_1, u_2, ..., u_n\} \subset \mathbb{R}^d[/math] — множество векторов
• [math]k \in \mathbb{N}[/math] — количество кластеров
• [math]\varepsilon[/math] — порог остановки (не обязательно).

Объём входных данных: [math]nd+1[/math].

Выходные данные:

• [math]M[/math] — матрица принадлежности векторов кластерам размера [math]nk[/math]. При этом данная матрица содержит только [math]n[/math] единиц, остальные значения ноль. Возможен вывод в другом виде, например, список списков.

Объём выходных данных: [math]nk[/math].

1.10 Свойства алгоритма

• Алгоритм не является детерминированным, так как инициализация кластеров происходит случайным образом, однако, ничто не мешает проводить инициализацию согласно некоторому детерминированному правилу.
• Алгоритм находит локальный оптимум, поэтому его обычно запускают несколько раз и выбирают лучший результат.
• Вычислительная мощность [math]\frac{kdi}{k+d}[/math]
• Алгоритм является устойчивым при одинаковой первоначальной инициализации — малая ошибка в начальных данных или при вычислениях очень незначительно повлияют на результат (скорее всего никак не повлияют). Тем не менее, при случайной инициализации результаты будут различны.
• Прост в реализации и вычислениях

2 Программная реализация

2.7 Существующие реализации алгоритма

• scikit-learn библиотека машинного обучения для языка Python.
• SciPy библиотека на языке Python, содержащая большое число реализаций различных алгоритмов.
• ELKI библиотека для анализа данных на языке программирования Java, содержит различные алгоритмы кластеризации.
• Spark распределённая версия алгоритма.
• MLPACK библиотека машинного обучения для C++.
• OpenCV библиотека содержит реализацию алгоритма.
• Apache Mahout содержит реализацию алгоритма на базе MapReduce.
• Weka библиотека и инструмент для анализа данных на языке Java.
• Torch библиотека машинного обучения на базе языка программирования Lua.
• Accord.NET содержит несколько различных реализаций на языке C#.
• R k-means реализация на языке R.

3 Литература

1. Jan Jantzen «Neurofuzzy Modelling». Электронное издание
2. Steinhaus H. (1956). Sur la division des corps materiels en parties. Bull. Acad. Polon. Sci., C1. III vol IV: 801—804.
3. Lloyd S. (1957). Least square quantization in PCM’s. Bell Telephone Laboratories Paper.
4. MacQueen J. (1967). Some methods for classification and analysis of multivariate observations. In Proc. 5th Berkeley Symp. on Math. Statistics and Probability, pages 281—297.