Участник:Шишков Илья Сергеевич/Алгоритм HCM (Hard C – Means)

Алгоритм HCM (Hard C – Means)
Последовательный алгоритм
Последовательная сложность	$O(ncK)$
Объём входных данных	$O(nK)$
Объём выходных данных	$O(c(K+n))$
Параллельный алгоритм
Высота ярусно-параллельной формы	$O(1)$
Ширина ярусно-параллельной формы	$O(cK)$

Основные авторы описания: Илья Шишков (1.1-1.4, 2.7), Гульгайша Темербекова (1.5-1.10, 3)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм HCM (Строгий алгоритм С-средних) был предложен группой исследователей(Jang, Sun and Mizutani) в 1997 и относится к классу алгоритмов со строгой кластеризаций.

Кластеризацией называется подход к описанию данных, в котором наиболее схожие данные объединяются в группы(кластеры). Кластеризация является распространенным подходом для анализа данных и используется во многих сферах научной деятельности, таких как машинное обучение, анализ данных, распознавание шаблонов, анализ изображений и биоинформатика.

Кластеризация представляет собой комбинирование рассматриваемых объектов так, чтобы каждая группа объектов обладала схожим свойством. В общем случае кластеризация характеризуются следующими критериями: - Каждая группа или кластер однородны; объекты, принадлежащие одной группе имеют схожие свойства; - Каждая группа или кластер отличаются от других кластеров т.е. объекты, принадлежащие одному кластеру, должны отличатся от объектов других кластеров

В строгой кластеризации наборы данных разделяются на кластеры однозначно. Каждый набор данных может относится только к одному кластеру. Строгой кластеризации характеризуется следующими свойствами: - Используется для классификации данных в однозначные наборы - Каждый набор данных принадлежит только одному кластеру - Кластеры также называют разделами - Результатом работы кластерного алгоритма является матрица соответствия которая показывает, к какому кластеру принадлежит каждый набор данных

В этом кластерном алгоритме не допускается частичное отношение к кластеру (как в FCM). HCM предназначен для классификации входных наборов в строгом смысле. В строгом алгоритме С-средних данные классифицируются по кластерам однозначно, т.е. при определенном заранее критерии, каждый элемент данных может принадлежать одному и только одному кластеру.

Алгоритм HCM является итеративным и состоит из нескольких шагов:

1.Инициализация:

Случайным образом определяются C векторов - центров кластеров

2. Расчет рядовой матрицы:

В процессе расчета рядовой матрицы каждый вектор сравнивается с ближайшим кластерным центром

3. Расчет оценочной функции:

Проверка условия, при котором алгоритм завершает работу и вывод результата в этом случае

4. Переопределение кластерных центров

Пункты 2-4 выполняются до тех пор, пока в пункте 3 проверка не станет успешной.

1.2 Математическое описание алгоритма

Обозначения

$U$ - наборы данных

$u_{i}$ - i-ый набор из $U$

$u$ - любой набор из $U$

$K$ - количество наборов в $U$

$c_{j}$ - j-ый кластер

$c$ - количество кластеров

$c_{j}$ - j-ый кластерный центр

$c^*_{j}$ - j-ый кластерный центр после обновления

Выходные данные: $c^*_{1}, c^*_{2}, ... c^*_{c}, M$

Объектная функция:

$J=\sum_{j = 1}^{c} \sum_{u_{i} \in C_{j}}^{} \|u_{i}-c_{j}\|^2, j \in 1,2, ... c, i={1,2, ...K}$

Шаг 1

Из входного набора $u_{1},u_{2}, ... u_{n}$ выбираются $c$ начальных кластерных центра $c_{1},c_{2},...,c_{c}$либо случайным образом, либо с использованием заранее определенного алгоритма

Шаг 2

Рассчитывается рядовая матрица $M=\|m_{ik}\|$ каждый элемент которой вычисляется по следующей формуле:

$m_{ik} = \begin{cases} 1, & \|u_k-c_i\|^2 \leqslant \|u_k-c_j\|^2 \;\; \text{for all } i \neq j; \;\; (i,j=1,2,\ldots,c; \; k = 1,2,\ldots,K)\\ 0, & \text{other}. \end{cases}$

Шаг 3

Рассчитывается объектная функция J. На этом этапе может быть инициировано завершение алгоритма в случае если значение объектной функции незначительно изменилось относительно предыдущей итерации или достигло ожидаемого значения.

Шаг 4

Рассчитываются новые кластерные центры по следующей формуле:

$c^*_{j} = \frac{1}{|C_{j}|} \sum_{u_{i} \in C_{j}}^{} c_{i}, j=1,2,3..,c$

где $|C_{j}|$ - число элементов, принадлежащих кластеру $C_{j}$

Шаг 5

Если алгоритм не завершил свою работу на шаге 3 то переходим к шагу 2.

1.3 Вычислительное ядро алгоритма

Вычислительным ядром данного алгоритма является вычисление на каждой итерации алгоритма квадратов норм между кластерными центрами и векторами из входного набор согласно формуле $\|u_k-c_i\|^2$. На каждой итерации алгоритма происходит $cK$ таких вычислений.

1.4 Макроструктура алгоритма

Основной операцией алгоритма является операция нахождения квадратов расстояний между исходными векторами и кластерными центрами.

$\|u_k-c_i\|^2$

При вычислении объектной функции производится суммирование полученных расстояний:

$J=\sum_{j = 1}^{c} \sum_{u_{i} \in C_{j}}^{} \|u_{i}-c_{j}\|^2, j \in 1,2, ... c, i={1,2, ...K}$

При перерасчете кластерных центров происходит суммирование векторов:

$c^*_{j} = \frac{1}{|C_{j}|} \sum_{u_{i} \in C_{j}}^{} u_{i}, j=1,2,3..,c$

1.5 Схема реализации последовательного алгоритма

Последовательность исполнения метода следующая :

1. Инициализация кластерных центров $c_i \, (i=1,2,\ldots,c)$. Это можно сделать выбрав случайным образом $c$ – векторов из входного набора.

2. Вычисление рядовой матрицы $M$:

$m_{ik} = \begin{cases} 1, & \|u_k-c_i\|^2 \leqslant \|u_k-c_j\|^2 \;\; \text{for all } i \neq j; \;\; (i,j=1,2,\ldots,c; \; k = 1,2,\ldots,K) \\ 0, & \text{other}. \end{cases}$

где К – количество элементов во входном наборе данных.

Матрица $M$ обладает следующими свойствами:

$\sum\limits_{i=1}^c m_{ij} = 1, \;\; \sum\limits_{j=1}^K m_{ij} = K.$

3. Расчёт объектной функции:

$J = \sum\limits_{i=1}^c J_i = \sum\limits_{i=1}^c \left( \sum\limits_{k:\, u_k \in C_i} \|u_k -c_i \|^2 \right) .$

На этом шаге происходит остановка и выход из цикла, если полученное значение ниже пороговой величины или полученное значение не сильно отличается от значений, полученных на предыдущих циклах.

4. Пересчёт кластерных центров выполняется в соответствии со следующим уравнением:

$c_i = \frac{1}{|C_i|} \sum\limits_{k:\, u_k \in C_i} u_k,$

где под $|C_i|$ подразумевается количество элементов в $i$-ом кластере.

5. на шаг 2.

1.6 Последовательная сложность алгоритма

Каждая операция вычисления квадрата нормы разности векторов выполненяет $n$ вычитаний, $n-1$ сложений и $n$ операций возведения в квадрат (умножений).

Для каждой итерации алгоритма требуется:

• $ncK$ умножений,
• $ncK$ вычитаний,
• $K(cn+1)$ сложений,
• $K(c-1)$ сравнений.

Умножения, сложения (вычитания), сравнения составляют основную часть алгоритма.

Итоговая сложность последовательной реализации алгоритма $O(ncK)$ . Обычно $n$, $c$ значительно меньше, чем $K$.

1.7 Информационный граф

опишем граф как аналитически, так и в виде рисунка.

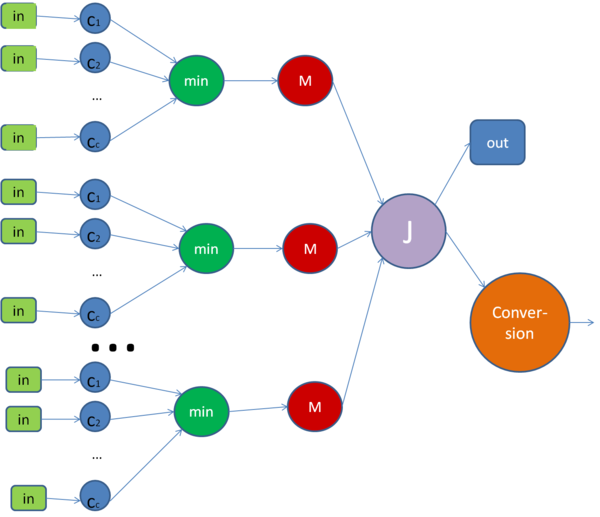
Граф алгоритма состоит из пяти групп вершин.

Первая группа вершин $c_1,...,c_c$ - прямое вычисление расстояния до кластерных центров, то есть вычисление расстояний от заданного элемента $u_i$ до каждого из кластерных центров.

Вторая группа вершин min - ей соответствует вычисление минимального расстояния до кластерных центров,передача найденного минимального расстояния и соответствующего ему индекса кластера.

Третья группа вершин M - ей соответствует операция записи единички в столбец матрицы.

Четвертая группа вершин J - вычисление объектной функции, происходит проверка условия достижения необходимой точности, если достигли заданной точности то переход в Out, в противном случае Conversion.

Пятая группа вершин Conversion - пересчёт кластерных центров и переход на следующую итерацию.

На рисунке изображена одна итерация алгоритма.

Рисунок 1. in - входные данные, $c_1,...,c_c$ - вычисление расстояния до кластерных центров и значение $u_i$ единое для каждой группы $c_1,...,c_c$, min - нахождение минимального расстояния до кластерных центров, M - запись единички в столбец матрицы, J - расчёт объектной функции, Conversion — пересчёт кластерных центров, out — вывод полученных данных.

1.8 Ресурс параллелизма алгоритма

Для одной итерации алгоритма в параллельном варианте требуется $K$ раз последовательно выполнить для каждого $u_i$ следующие ярусы:

• $C$ операций нахождения расстояния от элемента $u_i$ до каждого из кластерных центров.
• $C-1$ сравнений, для нахождения минимального расстояния.
• операция записи единички в столбец матрицы $M$.

Основным ресурсом алгоритма является вычисление квадрата нормы для каждого $u_i$. Расчёт значения объектной функции $J$ сложно представить в параллельном варианте, поэтому вычисление объектной функции производится последовательно.Использование параллельной реализации алгоритма приведёт к понижению производительности при небольшой размерности системы и малом объеме выборки. При параллельном варианте необходима пересылка данных, что при малом объеме выборки и небольшой размерности займет больше времени, чем при последовательном варианте. Как легко видеть из информационного графа, высота ЯПФ составляет $O(1)$, ширина ЯПФ составляет $O(cK)$, если число итераций меньше объема выборки.

1.9 Входные и выходные данные алгоритма

Входные данные:

1. $\{u_k\}_{k=1}^{K}$ — исходный набор векторов, принадлежащие пространству $\mathbb{R}^n$;
2. $c$ — количество кластеров;

Объём входных данных: $nK$.

Выходные данные:

1. $M$ — матрица, принадлежащая пространству $\mathbb{R}^{c \times K}$.
2. $\{c^*_i\}_{i=1}^{c}$ — набор построенных кластерных центров.

Объём выходных данных: $c(K+n)$.

1.10 Свойства алгоритма

Назначение: кластеризация больших наборов числовых данных.

Достоинства: легкость реализации,вычислительная простота.

Недостатки: задание количества кластеров,отсутствие гарантии в нахождении оптимального решения.

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

• Последовательная реализация на С++

• Последовательная реализация на MatLab