Участник:A.Freeman/Алгоритм Ланцоша для точной арифметики (без переортогонализации)

Алгоритм Ланцоша без переортогонализации
Последовательный алгоритм
Последовательная сложность	[math]O(kn^2)[/math]
Объём входных данных	[math]\frac{n (n + 1)}{2}+1[/math]
Объём выходных данных	[math]k(n+1)[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(k \log{n})[/math]
Ширина ярусно-параллельной формы	[math]O(n^2)[/math]

Основные авторы описания: Заспа А.Ю. (1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7), Фролов А.А. (1.6, 1.7, 1.8, 1.9, 1.10, 2.7)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм Ланцоша был опубликовн физиком и математиком Корнелием Ланцощем в 1950 году. Этот метод является частным случаем алгоритма Арнольда в случае, если исходная матрица [math]A[/math] - симметрична, и был представлен как итерационный метод вычисления собственных значений симметричной матрицы. Этот метод позволяет за [math]k[/math] итераций вычислять [math]k[/math] приближений собственных значений и собственных векторов исходной матрицы. Хотя алгоритм и был эффективным в вычислительном смысле, но он на некоторое время был предан забвению из-за численной неустойчивости. Только в 1970 Ojalvo и Newman модифицировали алгоритм для использования в арифметике с плавающей точкой. Новый метод получил название алгоритма Ланцоша с полной переортогонализацией. Но эта статья про его исходную версию. На вход алгоритма подается вещественная симметричная матрица [math]A = A^{T}[/math],

[math] A = \begin{pmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1\ n-1} & a_{1\ n} \\ a_{12} & a_{22} & a_{23} & \cdots & a_{2\ n-1} & a_{2\ n} \\ a_{13} & a_{23} & a_{33} & \cdots & a_{3\ n-1} & a_{3\ n} \\ \vdots & \vdots & \ddots & \ddots & \ddots & \vdots \\ a_{1\ n-1} & \cdots & \cdots & a_{n-2\ n-1} & a_{n-1\ n-1} & a_{n-1\ n} \\ a_{1\ n} & \cdots & \cdots & a_{n-2\ n} & a_{n-1\ n} & a_{n\ n} \\ \end{pmatrix} [/math]

Поэтому достаточно хранить только чуть больше половины элементов исходной матрицы.

Сам алгоритм соединяет в себя метод Ланцоша построения крыловского подпространства с процедурой Релея-Ритца. На каждой итерации строится матрица [math]Q_k = [q_1, q_2, \dots, q_k][/math] размерности [math]n \times k[/math], состоящая из ортонормированных векторов Ланцоша. А в качестве приближенных собственных значений берутся числа Ритца, т.е. собственные значения симметричной трехдиагональной матрицы [math]T_k = Q^T_k A Q[/math] размерности [math]k \times k[/math].

[math] T_k = \begin{pmatrix} \alpha_1 & \beta_1 \\ \beta_1 & \alpha_2 & \beta_2 \\ & \beta_2 & \ddots & \ddots \\ & & \ddots & \ddots & \beta_{k-1} \\ & & & \beta_{k-1} & \alpha_k \end{pmatrix} [/math]

Нахождение собственных значений и собственных векторов такой матрицы значительно проще чем их вычисление для исходной матрицы. Например, они могут быть вычислены с помощью метода «разделяй и властвуй» вычисления собственных значений и векторов симметричной трехдиагональной матрицы. В этом методе эта процедура занимает [math]O(k^3)[/math] операций, где константа оказывается на практике довольно мала.

1.2 Математическое описание алгоритма

Исходные данные: симметрическая матрица [math]A[/math], начальный вектор [math]b[/math].

Вычисляемые данные: собственные вектора матрицы [math]T_k[/math] являющиеся столбцами матрицы [math]Q_k V[/math], и матрица собственных значений [math]\Lambda[/math], где [math]V, \Lambda[/math] из спектрального разложения [math]T_k = V\Lambda V^T[/math]. До начала первой итерации нормируется вектор начального приближения [math]q_1 = \frac{b}{\|b\|_2}[/math]. Затем задаются константы [math]\beta_0 = 0,\; q_0 = 0 [/math].

После выполнения данных действий начинаются итерации алгоритма. Которых будет не больше чем [math]k[/math]. В ходе итераций постепенно формируется матрица [math]T_k[/math] из [math]\alpha_i[/math]-x и [math]\beta_i[/math]-х.

На [math]i[/math]-й итерации происходят следующие вычисления. Вначале вычисляется произведение матрицы на вектор [math]z = Aq_i[/math]. Затем считается скалярное произведение [math]\alpha_i = q^T_i z[/math] и значение сохраняется как элемент формируемой матрицы. После этого необходимо произвести вычисление линейной комбинации векторов [math]z = z - \alpha_i q_i - \beta_{i-1}q_{i-1}[/math]. Норму полученного вектора запишем как элемент матрицы [math]\beta_i = \|z\|_2[/math]. Если [math]\beta_i[/math] оказалась равной нулю, то больше никаких итераций в алгоритме не производят, сразу переходят к вычислению собственных значений и собственных векторов. Иначе, в конце итерации считают [math]q_{i+1} = \frac{z}{\beta_i}[/math] и переходят к следующей итерации.

После всех итераций необходимо вычислить собственные значения и собственные вектора матрицы [math]T_k[/math].

1.3 Вычислительное ядро алгоритма

Вычислительным ядром на каждой итерации является вычисление произведения матрицы на вектор:

[math]z = Aq_i[/math]

1.4 Макроструктура алгоритма

Макрооперациями алгоритма являются:

• умножение матрицы на вектор. Состоит из операций умножения вектора на число и сложения векторов.
• скалярное произведение векторов.
• линейная комбинация векторов. Состоит из умножений вектора на число и сложений векторов.
• получение нормы вектора. Состоит из скалярного произведения векторов, вычисления квадратного корня.
• деление вектора на число.
• вычисление собственных векторов и собственных значений трехдиагональной симметричной матрицы.

1.5 Схема реализации последовательного алгоритма

Последовательность исполнения метода следующая:

[math]1.\, \beta_0 = 0,\; q_0 = 0[/math] #Инициализируются константы

[math]2.\, \|b\|_2 = \sqrt{\sum\limits_{j=1}^{n} b_j^2}[/math] #Вычисляем норму вектора начального приближения.

[math]3.\, q_{1_{j}} = \frac{b_{j}}{\|b\|_2}, \; j = 1,\, \dots\,, n[/math] #Нормализуем вектор начального приближения.

Начинаются итерации цикла, которых не больше чем [math]k[/math]. На [math]i[/math]-й итерации производятся следующие вычисления:

[math]i.1\, z_j = \sum\limits_{m=1}^{n} a_{jm} q_{i_m}, \; j = 1,\,\dots\,, n[/math] #Считаем результат применения линейного оператора [math]A[/math] к вектору [math]q_i[/math].

[math]i.2\, \alpha_i = \sum\limits_{j=1}^{n}q_{i_j} z_j[/math] #Получаем результат скалярного произведения векторов [math]q_i[/math] и [math]z[/math].

[math]i.3\, z_j = z_j - \alpha_i q_{i_j} - \beta_{i-1}q_{i-1_j}, \, j = 1,\,\dots\,, n[/math] #Вычисляем линейную комбинацию векторов.

[math]i.4\, \beta_i = \|z\|_2 = \sqrt{\sum\limits_{j=1}^{n} z_j^2}[/math] #Считаем норму вектора [math]z[/math].

[math]i.5[/math] Проверка равенства [math]\beta_i == 0[/math] # Если норма оказалась равной нулю, то завершаем итерации и переходим к вычислению собственных векторов и собственных значений полученной матрицы. В обратном случае, продолжаем выполнения итераций.

[math]i.6\, q_{i+1_j} = \frac{z_j}{\beta_i}, \; j = 1,\, \dots \,, n[/math] #Нормируем вектор [math]z[/math].

[math]i.7\,[/math] Если выполнили [math]k[/math] итераций, то завершаем выполнение итераций, переходим к следующему шагу. Иначе начинаем последующую итерацию цикла.

[math]4.[/math] Вычисляем собственные значения и собственные вектора полученной матрицы [math]T_k[/math].

1.6 Последовательная сложность алгоритма

Вычисления [math]k[/math] собственных значений матрицы порядка [math]n[/math] и соответствующих им собственных векторов алгоритмом Ланцоша без переортогонализации состоит из инициализации, [math]k[/math] итераций и нахождения собственных значений и векторов трехдиагональной симметричной матрицы порядка [math]k[/math].

Инициализация состоит из следующих операций:

• вычисление нормы:
  • [math]n^2[/math] операций умножения
  • [math]n-1[/math] операций сложений
  • извлечение квадратного корня
• [math]n[/math] операций делений (нормирование)

Каждая из [math]k[/math] итераций состоит из:

• умножение матрицы на вектор:
  • [math]n^2[/math] умножений
  • [math]n(n-1)[/math] сложений
• скалярное произведение двух векторов
  • [math]n[/math] умножений
  • [math]n-1[/math] сложение
• вычисление линейной комбинации векторов:
  • [math]2n[/math] умножений
  • [math]2n[/math] вычитаний
• норма вектора:
  • [math]n[/math] операций умножения
  • [math]n-1[/math] операций сложений
  • извлечение квадратного корня
• нормирование вектора:
  • [math]n[/math] операций деления

Итого (без учета решения трехдиагональной матрицы):

• [math] k(n^2 + 4n) + n [/math] умножений,
• [math] k(n^2+3n-2) + n-1[/math] сложений/вычитаний,
• [math] kn + n [/math] делений,
• [math] k + 1 [/math] вычислений квадратного корня.

Умножения и сложения (вычитания) составляют основную часть алгоритма.

Для нахождение собственных значений и векторов трехдиагональной симметричной матрицы эффективней всего использовать метод «разделяй и властвуй» вычисления собственных значений и векторов симметричной трехдиагональной матрицы, который требует [math] O(k^3) [/math] операций. При классификации по последовательной сложности, таким образом, метод Ланцоша без переортогонализации относится к алгоритмам с квадратичной сложностью.

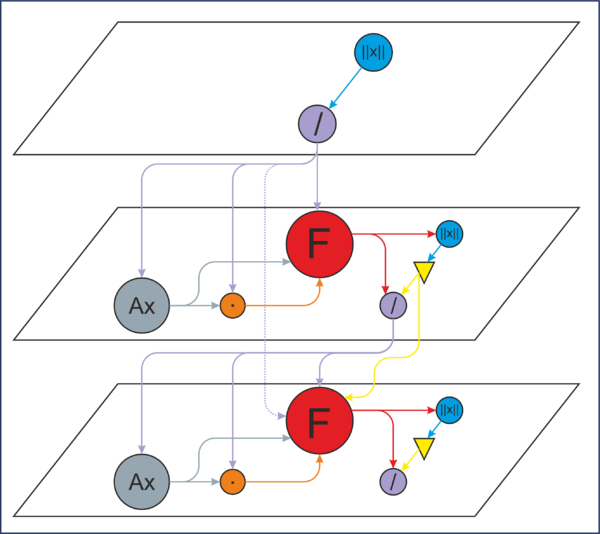
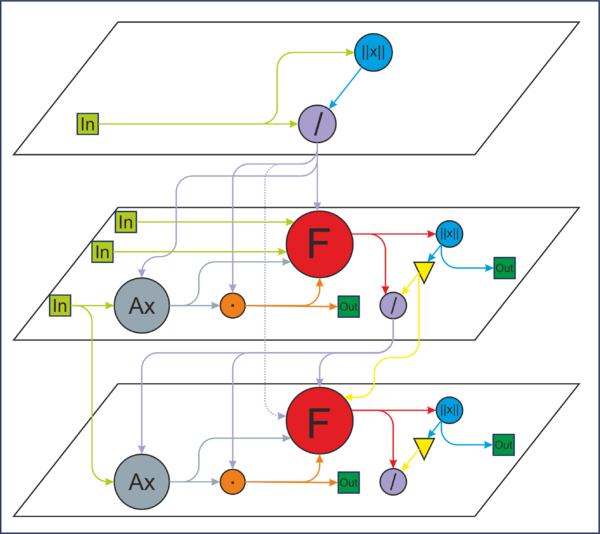
1.7 Информационный граф

Рисунок 1. Граф алгоритма без отображения входных и выходных данных. [math]\|x\|[/math] — макрооперация взятия нормы, [math]/[/math] — операция деления, [math]\cdot [/math] — операция умножения, [math]\mathsf{F}[/math] — вычисление линейной комбинации векторов, [math]\mathsf{Ax}[/math] — линейный оператор, [math]\nabla[/math] — условие преждевременного выхода.

Рисунок 2. Граф алгоритма с отображением входных и выходных данных. [math]\|x\|[/math] — макрооперация взятия нормы, [math]/[/math] — операция деления, [math]\cdot [/math] — операция умножения, [math]\mathsf{F}[/math] — вычисление линейной комбинации векторов, [math]\mathsf{Ax}[/math] — линейный оператор, [math]\nabla[/math] — условие преждевременного выхода, [math]\mathsf{In}[/math] — входные данные, [math]\mathsf{Out}[/math] — выходные результат.

Рисунок 3. Граф линейного оператора без отображения входных и выходных данных.
[math]*[/math] — операция умножения двух коэффициентов,
[math]+[/math] — операция сложения.

1.8 Ресурс параллелизма алгоритма

Алгоритм Ланцоша в параллельной форме состоит из инициализации, [math]k[/math] итераций и вычисления собственных значений матрицы [math]T_k[/math], рассмотрение которого выходит за рамки данной статьи.

Заметим, что вычисление суммы [math]n[/math] элементов имеет высоту [math]\log n[/math] и линейную ширину ярусов [math]\frac{n}{2}, \frac{n}{4}, ... , 1[/math].

Инициализации состоит из следующих операций:

• вычисление нормы:
  • вычисление скалярного произведения вектора самого на себя:
    • ярус умножений шириной [math]n[/math]
    • [math]\log{n}[/math] ярусов сложений с наибольшей шириной [math]\frac{n}{2}[/math]
  • ярус извлечения квадратного корня с единичным вычислением
• деление вектора на число (нормирование вектора):
  • ярус [math]n[/math] операций деления

Итерационная часть алгоритма состоит из следующих операций:

• умножение матрицы на число:
  • ярус умножений с шириной [math]n^2[/math]
  • [math]\log n[/math] ярусов с наибольшей шириной [math]\frac{n^2}{2}[/math] (блок вычисления n сумм n элементов)
• вычисление скалярного произведения двух векторов:
  • ярус умножений шириной [math]n[/math]
  • [math]\log{n}[/math] ярусов сложений с наибольшей шириной [math]\frac{n}{2}[/math]
• вычисление линейной комбинации векторов:
  • ярус умножений шириной [math]2n[/math]
  • два яруса сложений шириной [math]n[/math]
• вычисление нормы:
  • вычисление скалярного произведения вектора самого на себя:
    • ярус умножений шириной [math]n[/math]
    • [math]\log{n}[/math] ярусов сложений с максимальной шириной [math]\frac{n}{2}[/math]
  • ярус извлечения квадратного корня с единичным вычислением
• проверка на выход из цикла
• деление вектора на число (нормирование вектора, может отсутствовать на последней итерации):
  • ярус [math]n[/math] операций деления

Таким образом, в параллельном варианте основную долю времени будут занимать операции сложения при умножении матрицы на вектор. При классификации по высоте ЯПФ Алгоритм Ланцоша относится к алгоритмам со сложностью [math]O(k \log n)[/math]. При классификации по ширине ЯПФ его сложность будет [math]O(n^2)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: симметричная матрица [math]A[/math] (элементы [math]a_{ij}, i \geq j[/math]), число [math]k[/math].

Объём входных данных: [math]\frac{n (n + 1)}{2} + 1[/math] (в силу симметричности достаточно хранить только диагональ и над/поддиагональные элементы, единица относится к параметру [math]k[/math]).

Выходные данные: по [math]k[/math] приближений собственных значений и собственных векторов.

Объём выходных данных: [math]k+kn[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является субквадратичным: [math]\frac{kn^2}{k \log{n}}[/math].

Алгоритм Ланцоша без переортогонализации не является детерминированным (возможно выполнение меньшего числа итераций алгоритма), в случае если все собственные значения уже вычислены.

Важное свойство метода Ланцоша состоит в том, что первыми в матрице [math]T_{j}[/math] появляются собственные значения с максимальной величиной по модулю. Таким образом, метод особенно хорошо подходит для вычисления собственных значений матрицы [math]A[/math], находящихся на краях её спектра.

2 Программная реализация

2.7 Существующие реализации

Реализация в проекте IETL

Реализация в проекте ARPACK