Участник:Alexbashirov/Алгоритм Ланцоша для точной арифметики

Авторы: Баширов А.Д.

Алгоритм Ланцоша для точной арифметики
Последовательный алгоритм
Последовательная сложность	$O(kn^2)$.
Объём входных данных	$n^2 + n + 1$
Объём выходных данных	$k$
Параллельный алгоритм
Высота ярусно-параллельной формы	$O(n)$
Ширина ярусно-параллельной формы	$O(n^2)$

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

1.1.1 История

Алгоритм Ланцоша является прямым алгоритмом поиска собственных значений симметричной матрицы, разработанным венгерским физиком и математиком XX столетия Корнелием Ланцошем в 1950 году. Алгоритм совмещает в себе два других алгоритма: алгоритм построения подпространства Крылова (который также был создан Ланцошем) и процедуру Рэлея-Ритца приближения собственных значений матрицы. Алгоритм является вариацией степенного метода, позволяющего найти собственные значения и собственные вектора матрицы $n$-го порядка. Однако в алгоритме число итераций ограничено некоторым $k$, где $k\lt \lt n$. Несмотря на заявленную вычислительную эффективность, алгоритм не получил широкого применения в своём первоначальном виде, ввиду его неустойчивости. 20 лет спустя, в 1970 году ученые Ojalvo и Newman показали доработанный алгоритм Ланцоша, который теперь стал устойчивым а также предложили способ выбора вектора начального приближения $v_0$. Полученный последователями Ланцоша алгоритм получил название "Алгоритм Ланцоша с полной переортогонализацией".

1.2 Математическое описание алгоритма

Алгоритм Ланцоша работает с вещественной симметричной матрицей $A=A^T$, таким образом в памяти достаточно хранить лишь немногим более половины элементов матрицы $A$.

Прежде чем переходить к описанию алгоритма, следует упомянуть следующие понятия: подпространство Крылова и процесс Рэлея-Ритца, о которых уже было сказано в исторической справке выше. Подпространством Крылова называется набор векторов$K_n =[b,Ab,A^2b,...,A^{n-1}b]$. Начав свою работу с произвольного вектора $b$, степенной метод вычисляет вектора $Ab, A^2b,...,A^{n-1}b$ итерационно сохраняя полученный результат в вектор $b$. Полученная последовательность векторов сходится к собственному вектору, отвечающему максимальному собственному значению $\lambda_{max}$. Однако, использование лишь последнего полученного вектора и потеря всех предшествующих посчитанных величин не всегда является наилучшим выбором. Поэтому сохранив все вектора и объединив их в одну матрицу мы получим так называемую матрицу Крылова:

$K_j = [b,Ab,A^2b,...,A^{j-1}b]$.

Столбцы получившейся матрицы не ортогональны, однако их можно ортогонализовать, применив процесс Грамма-Шмидта. Получившиеся вектора будут составлять базис подпространства Крылова $Q_j$. Можно ожидать, что вектора полученного базиса будут достаточно хорошо приближать $j$ собственных векторов, отвечающих $j$ наибольшим собственным значения.

Затем с использованием полученной матрицы из ортогональных векторов $Q_j$ мы получим трехдиагональную матрицу $T_j$ на основе исходной матрицы $A$: $T_j=Q_j^TAQ_j$. Наконец, к полученной матрице $T_j$ будет применяться процесс Рэлея-Ритца, который найдет собственные значения трехдиагональной матрицы. В последствии эти значения и будут приближениями искомых собственных значений исходной матрицы $A$.

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма Ланцоша, то есть наиболее ресурсно-затратной частью алгоритма, является шаг на котором на каждой итерации происходит перемножение матрицы $A$ на вектор $q_j$, полученный на предыдущей итерации. Полученный в результате умножения вектор обозначается $z$:

$z=Aq_j$.

1.4 Макроструктура алгоритма

Как уже говорилось в математическом описании, алгоритм объединяет в себе два алгоритма: метод построения подпространства Крылова и процедуру поиска собственных значений трехдиагональной матрицы (процес Рэлея-Ритца).

Первую составную часть (алгоритм построения подпространства Крылова) представляет итерационный процесс построения матрицы $Q_j=[q_1,q_2,...q_j]$ из $j$ ортонормированных вектров Ланцоша и последующее формирование трехдиагональной матрицы $T_j=Q_j^TAQ_j$. Число таких векторов и, следовательно, размер матрицы растет с каждой итерацией. Итерационный процесс завершается при $j=k$.

На долю второй части алгоритма приходится поиск собственных значений и соответствующих им собственных векторов матрицы $T_j=Q_j^TAQ_j$, полученной в первой части.

1.5 Схема последовательной реализации алгоритма

На рисунке выше представлен псевдокод, отражающий последовательность действий в алгоритме метода. Перечислим основные ступени в данном методе:

• Прежде чем войти в цикл, происходит инициализация констант $\Beta_0,q_0$, вычисление нормы вектора начального приближения $b$ и нормализация этого вектора.
• Затем, в цикле, происходит:
  • поиск вектора $z$, являющегося результатом применения матричного оператора $A$ к вектору $q_j$;
  • скалярное произведение двух векторов $q_j$ и $z$;
  • вычисляется линейная комбинация векторов;
  • вычисляется норма вектора $z$;
  • проверяется условие выхода из цикла (равенство нулю нормы вектора $z$);
  • в случае если норма не нулевая, то производим нормировку вектора;
  • затем происходит процедура поиска собственных значений и векторов матрицы $T_j$
  • и, наконец, переход на следующий шаг цикла.

1.6 Последовательная сложность алгоритма

Посчитаем количество операций, необходимых для поиска $k$ собственных значений и векторов для матрицы $A$ размерности $n\times n$.

• $n^2$ действий для умножения матрицы на вектор
• $n$ действия для перемножения двух векторов
• $n$ операций для поэлементного сложения или вычитания двух векторов
• для отыскания нормы вектора помимо $n$ сложений и $n$ умножений требуется 1 операция извлечения корня
• для поиска собственных значений и векторов матрицы $T_j$ требуется $O(k^3)$ операций.

Суммарно для одной итерации алгоритма требуется совершить $O(n^2)+O(k^3)$ операций.

1.7 Информационный граф

В данном разделе приведен информационный граф одной итерации алгоритма Ланцоша. Для простоты на схеме подразумевается матрица размерности 5x5, однако это не нарушает общности данной схемы.

Круглые элементы символизируют операции с элементами векторов и матриц: сложение и умножение (черные), операции составления линейной комбинации (зеленые) и операции деления вектора на его норму. В квадратных элементах изображены операции, которые невозможно выполнить параллельно: нахождение суммы элементов вектора (синий) и вычисление нормы вектора (красный).

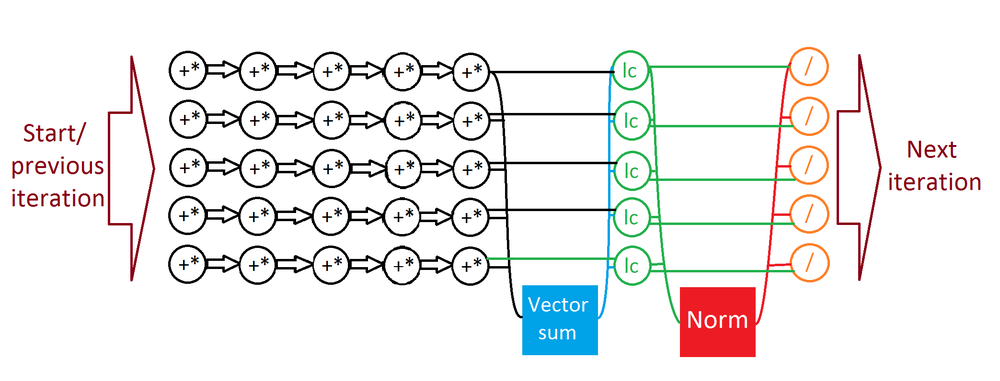
1.8 Ресурс параллелизма алгоритма

Поскольку алгоритм является итерационным, то выполнять параллельные операции возможно только внутри каждой итерации алгоритма. Сами итерации выполняются в строгой последовательности и не могут быть параллелизованны. Однако внутри каждой итерации происходят два процесса, которые могут быть параллелизованны:

• умножение матрицы на вектор,
• процесс поиска собственных значений.

Умножение квадратной матрицы размерности $n\times n$ на вектор размерности $n$ требует $n$ ярусов умножений и сложений. В свою очередь ресурс параллелизма операции поиска собственных значений зависит от выбранного способа и не рассматривается в данной статье.

Таким образом, с точки зрения ресурса параллелизма, алгоритм Ланцоша обладает линейной сложностью по ширине ЯПФ и квадратичной сложностью по высоте ЯПФ. Основное время работы алгоритма будет уделено операции умножения матрицы на вектор, имеющей ширину яруса $n^2$.

1.9 Входные и выходные данные алгоритма

Алгоритм призван найти фиксированное число $k$ первых собственных значений матрицы $A$, следовательно на вход данный алгоритм во всяком случае получает 1 число и 1 матрицу размерности $n\times n$. Помимо этого для начала работы алгоритму нужен некоторый вектор $b_0$ начального приближения размерности $n$, который тоже является входными данными.

После окончания работы алгоритма мы получаем набор собственных значений матрицы $A$, состоящий из $k$ элементов. Если помимо собственных значений выводятся еще и полученные собственные векторы, то суммарный объём всех таких векторов составляет $k\times n$ элементов.

Таким образом, совокупный объём входных данных составляет: $n^2+n+1$ элемент, а на выходе получаем $k(n+1)$ элементов.

1.10 Свойства алгоритма

Преимуществом алгоритма является то, что он начинает поиск собственных значений матрицы $T_j$ (а значит и матрицы $A$) начиная с максимального в абсолютном смысле значения. Это выгодно отличает данный алгоритм с точки зрения поиска собственных значений матрицы, находящихся по краям её спектра.

Не является полностью детерминированным, т.к. может досрочно завершить работу, если будут найдены все ненулевые собственные значения.

В случае использования метода вычисления собственных значений с линейной сложностью, соотношение последовательной и параллельной сложностей будет равно $(k ^ 2 + n ^ 2) / (k + n)$.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

TODO

2.7 Существующие реализации алгоритма

В настоящее время алгоритм Ланцоша поиска собственных значений квадратной симметричной матрицы включён в несколько библиотек и реализован на различных языках, среди которых такие наиболее распространенные как C, C++, FORTRAN77/90, MathLab. Так, например, в языке MathLab во встроенном пакете ARPACK найти собственные значения методом Ланцоша можно при помощи вызова функции eigs().

На языке С существует библиотека PRIMME, название которой расшифровывается как PReconditioned Iterative MultiMethod Eigensolver (итерационные методы поиска собственных значений с предусловием).

Библиотека NAG Numerical Library также содержит обширный набор функций, позволяющих проводить математический анализ, среди которых есть и реализация алгоритма Ланцоша. Библиотека доступна в трех пакетах: NAG C Library, NAG Fortran Library и NAG Library for .NET, совместна со многими языками и с основными операционными системами (Windows, Linux and OS X, а также Solaris, AIX и HP-UX).

3 Литература

[1] Дж. Деммель «Вычислительная линейная алгебра», с 381.

[2] Wikipedia https://en.wikipedia.org/wiki/Lanczos_algorithm

[3] "Investigation and Implementation of an Eigensolver Method", Jorge Moreira, The University of Edinburgh, August 2014

[4] "Lanczos Vector Procedures", Travis Hoppe