Участник:Шишков Илья Сергеевич/Алгоритм HCM (Hard C – Means)

Эта работа прошла предварительную проверку Дата последней правки страницы: 01.11.2016 Данная работа соответствует формальным критериям. Проверено Coctic.

Алгоритм HCM (Hard C – Means)
Последовательный алгоритм
Последовательная сложность	[math]O(ncK)[/math]
Объём входных данных	[math]O(nK)[/math]
Объём выходных данных	[math]O(c(K+n))[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(1)[/math]
Ширина ярусно-параллельной формы	[math]O(cK)[/math]

Основные авторы описания: Илья Шишков (1.1-1.4, 2.7), Гульгайша Темербекова (1.5-1.10, 3)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм HCM (Строгий алгоритм С-средних) был предложен группой исследователей(Jang, Sun and Mizutani) в 1997 и относится к классу алгоритмов со строгой кластеризаций.

Кластеризацией называется подход к описанию данных, в котором наиболее схожие данные объединяются в группы(кластеры). Кластеризация является распространенным подходом для анализа данных и используется во многих сферах научной деятельности, таких как машинное обучение, анализ данных, распознавание шаблонов, анализ изображений и биоинформатика.

Кластеризация представляет собой комбинирование рассматриваемых объектов так, чтобы каждая группа объектов обладала схожим свойством. В общем случае кластеризация характеризуются следующими критериями: - Каждая группа или кластер однородны; объекты, принадлежащие одной группе имеют схожие свойства; - Каждая группа или кластер отличаются от других кластеров т.е. объекты, принадлежащие одному кластеру, должны отличатся от объектов других кластеров

В строгой кластеризации наборы данных разделяются на кластеры однозначно. Каждый набор данных может относится только к одному кластеру. Строгой кластеризации характеризуется следующими свойствами: - Используется для классификации данных в однозначные наборы - Каждый набор данных принадлежит только одному кластеру - Кластеры также называют разделами - Результатом работы кластерного алгоритма является матрица соответствия которая показывает, к какому кластеру принадлежит каждый набор данных

В этом кластерном алгоритме не допускается частичное отношение к кластеру (как в FCM). HCM предназначен для классификации входных наборов в строгом смысле. В строгом алгоритме С-средних данные классифицируются по кластерам однозначно, т.е. при определенном заранее критерии, каждый элемент данных может принадлежать одному и только одному кластеру.

Алгоритм HCM является итеративным и состоит из нескольких шагов:

1.Инициализация:

Случайным образом определяются C векторов - центров кластеров

2. Расчет рядовой матрицы:

В процессе расчета рядовой матрицы каждый вектор сравнивается с ближайшим кластерным центром

3. Расчет оценочной функции:

Проверка условия, при котором алгоритм завершает работу и вывод результата в этом случае

4. Переопределение кластерных центров

Пункты 2-4 выполняются до тех пор, пока в пункте 3 проверка не станет успешной.

1.2 Математическое описание алгоритма

Обозначения

[math]U[/math] - наборы данных

[math]u_{i}[/math] - i-ый набор из [math]U[/math]

[math]u[/math] - любой набор из [math]U[/math]

[math]K[/math] - количество наборов в [math]U[/math]

[math]c_{j}[/math] - j-ый кластер

[math]c[/math] - количество кластеров

[math]c_{j}[/math] - j-ый кластерный центр

[math]c^*_{j}[/math] - j-ый кластерный центр после обновления

Выходные данные: [math]c^*_{1}, c^*_{2}, ... c^*_{c}, M[/math]

Объектная функция:

[math]J=\sum_{j = 1}^{c} \sum_{u_{i} \in C_{j}}^{} \|u_{i}-c_{j}\|^2, j \in 1,2, ... c, i={1,2, ...K}[/math]

Шаг 1

Из входного набора [math]u_{1},u_{2}, ... u_{n}[/math] выбираются [math]c[/math] начальных кластерных центра [math] c_{1},c_{2},...,c_{c}[/math]либо случайным образом, либо с использованием заранее определенного алгоритма

Шаг 2

Рассчитывается рядовая матрица [math] M=\|m_{ik}\|[/math] каждый элемент которой вычисляется по следующей формуле:

[math] m_{ik} = \begin{cases} 1, & \|u_k-c_i\|^2 \leqslant \|u_k-c_j\|^2 \;\; \text{for all } i \neq j; \;\; (i,j=1,2,\ldots,c; \; k = 1,2,\ldots,K)\\ 0, & \text{other}. \end{cases} [/math]

Шаг 3

Рассчитывается объектная функция J. На этом этапе может быть инициировано завершение алгоритма в случае если значение объектной функции незначительно изменилось относительно предыдущей итерации или достигло ожидаемого значения.

Шаг 4

Рассчитываются новые кластерные центры по следующей формуле:

[math] c^*_{j} = \frac{1}{|C_{j}|} \sum_{u_{i} \in C_{j}}^{} c_{i}, j=1,2,3..,c[/math]

где [math]|C_{j}| [/math] - число элементов, принадлежащих кластеру [math]C_{j}[/math]

Шаг 5

Если алгоритм не завершил свою работу на шаге 3 то переходим к шагу 2.

1.3 Вычислительное ядро алгоритма

Вычислительным ядром данного алгоритма является вычисление на каждой итерации алгоритма квадратов норм между кластерными центрами и векторами из входного набор согласно формуле [math]\|u_k-c_i\|^2[/math]. На каждой итерации алгоритма происходит [math]cK[/math] таких вычислений.

1.4 Макроструктура алгоритма

Основной операцией алгоритма является операция нахождения квадратов расстояний между исходными векторами и кластерными центрами.

[math] \|u_k-c_i\|^2 [/math]

При вычислении объектной функции производится суммирование полученных расстояний:

[math]J=\sum_{j = 1}^{c} \sum_{u_{i} \in C_{j}}^{} \|u_{i}-c_{j}\|^2, j \in 1,2, ... c, i={1,2, ...K}[/math]

При перерасчете кластерных центров происходит суммирование векторов:

[math] c^*_{j} = \frac{1}{|C_{j}|} \sum_{u_{i} \in C_{j}}^{} u_{i}, j=1,2,3..,c[/math]

1.5 Схема реализации последовательного алгоритма

Последовательность исполнения метода следующая :

1. Инициализация кластерных центров [math]c_i \, (i=1,2,\ldots,c)[/math]. Это можно сделать выбрав случайным образом [math]c[/math] – векторов из входного набора.

2. Вычисление рядовой матрицы [math]M[/math]:

[math] m_{ik} = \begin{cases} 1, & \|u_k-c_i\|^2 \leqslant \|u_k-c_j\|^2 \;\; \text{for all } i \neq j; \;\; (i,j=1,2,\ldots,c; \; k = 1,2,\ldots,K) \\ 0, & \text{other}. \end{cases} [/math]

где К – количество элементов во входном наборе данных.

Матрица [math]M[/math] обладает следующими свойствами:

[math] \sum\limits_{i=1}^c m_{ij} = 1, \;\; \sum\limits_{j=1}^K m_{ij} = K. [/math]

3. Расчёт объектной функции:

[math] J = \sum\limits_{i=1}^c J_i = \sum\limits_{i=1}^c \left( \sum\limits_{k:\, u_k \in C_i} \|u_k -c_i \|^2 \right) .[/math]

На этом шаге происходит остановка и выход из цикла, если полученное значение ниже пороговой величины или полученное значение не сильно отличается от значений, полученных на предыдущих циклах.

4. Пересчёт кластерных центров выполняется в соответствии со следующим уравнением:

[math] c_i = \frac{1}{|C_i|} \sum\limits_{k:\, u_k \in C_i} u_k, [/math]

где под [math]|C_i|[/math] подразумевается количество элементов в [math]i[/math]-ом кластере.

5. на шаг 2.

1.6 Последовательная сложность алгоритма

Каждая операция вычисления квадрата нормы разности векторов выполненяет [math]n[/math] вычитаний, [math]n-1[/math] сложений и [math]n[/math] операций возведения в квадрат (умножений).

Для каждой итерации алгоритма требуется:

• [math]ncK[/math] умножений,
• [math]ncK[/math] вычитаний,
• [math]K(cn+1)[/math] сложений,
• [math]K(c-1)[/math] сравнений.

Умножения, сложения (вычитания), сравнения составляют основную часть алгоритма.

Итоговая сложность последовательной реализации алгоритма [math]O(ncK)[/math] . Обычно [math]n[/math], [math]c[/math] значительно меньше, чем [math]K[/math].

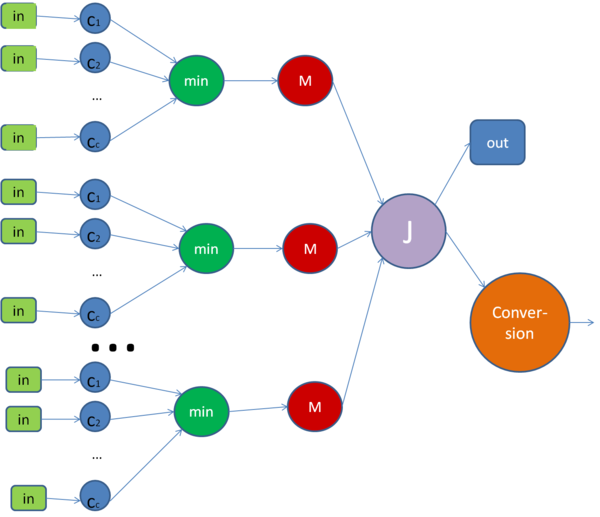
1.7 Информационный граф

опишем граф как аналитически, так и в виде рисунка.

Граф алгоритма состоит из пяти групп вершин.

Первая группа вершин [math]c_1,...,c_c[/math] - прямое вычисление расстояния до кластерных центров, то есть вычисление расстояний от заданного элемента [math]u_i[/math] до каждого из кластерных центров.

Вторая группа вершин min - ей соответствует вычисление минимального расстояния до кластерных центров,передача найденного минимального расстояния и соответствующего ему индекса кластера.

Третья группа вершин M - ей соответствует операция записи единички в столбец матрицы.

Четвертая группа вершин J - вычисление объектной функции, происходит проверка условия достижения необходимой точности, если достигли заданной точности то переход в Out, в противном случае Conversion.

Пятая группа вершин Conversion - пересчёт кластерных центров и переход на следующую итерацию.

На рисунке изображена одна итерация алгоритма.

Рисунок 1. in - входные данные, [math]c_1,...,c_c[/math] - вычисление расстояния до кластерных центров и значение [math]u_i[/math] единое для каждой группы [math]c_1,...,c_c[/math], min - нахождение минимального расстояния до кластерных центров, M - запись единички в столбец матрицы, J - расчёт объектной функции, Conversion — пересчёт кластерных центров, out — вывод полученных данных.

1.8 Ресурс параллелизма алгоритма

Для одной итерации алгоритма в параллельном варианте требуется [math]K[/math] раз последовательно выполнить для каждого [math]u_i[/math] следующие ярусы:

• [math]C[/math] операций нахождения расстояния от элемента [math]u_i[/math] до каждого из кластерных центров.
• [math]C-1[/math] сравнений, для нахождения минимального расстояния.
• операция записи единички в столбец матрицы [math]M[/math].

Основным ресурсом алгоритма является вычисление квадрата нормы для каждого [math]u_i[/math]. Расчёт значения объектной функции [math]J[/math] сложно представить в параллельном варианте, поэтому вычисление объектной функции производится последовательно.Использование параллельной реализации алгоритма приведёт к понижению производительности при небольшой размерности системы и малом объеме выборки. При параллельном варианте необходима пересылка данных, что при малом объеме выборки и небольшой размерности займет больше времени, чем при последовательном варианте. Как легко видеть из информационного графа, высота ЯПФ составляет [math]O(1)[/math], ширина ЯПФ составляет [math]O(cK)[/math], если число итераций меньше объема выборки.

1.9 Входные и выходные данные алгоритма

Входные данные:

1. [math]\{u_k\}_{k=1}^{K}[/math] — исходный набор векторов, принадлежащие пространству [math]\mathbb{R}^n[/math];
2. [math]c[/math] — количество кластеров;

Объём входных данных: [math]nK[/math].

Выходные данные:

1. [math]M[/math] — матрица, принадлежащая пространству [math]\mathbb{R}^{c \times K}[/math].
2. [math]\{c^*_i\}_{i=1}^{c}[/math] — набор построенных кластерных центров.

Объём выходных данных: [math]c(K+n)[/math].

1.10 Свойства алгоритма

Назначение: кластеризация больших наборов числовых данных.

Достоинства: легкость реализации,вычислительная простота.

Недостатки: задание количества кластеров,отсутствие гарантии в нахождении оптимального решения.

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

• Последовательная реализация на С++

• Последовательная реализация на MatLab